Conclusion

While I have made a lot of progress since the start of this project, I am disappointed that I don’t have more time to work on it because I made so much progress right at the end, finally figuring out techniques that worked well in Mathematica. If I had more time I would try to make some contours of multiple dipoles, and see how things cancel out. Admittedly this would be a lot harder to picture the perpendicular field lines, and the 3D structure would probably become more necessary. Its also possible that the contour technique I used here might not work well at all for multiple dipoles, but it would have been good to check it out a bit at least.

That being said, I did make some pretty cool 3D graphs of magnetic equipotential surfaces that scale as expected with current intensity. The 2D case helped greatly to show how these contour surfaces represent the magnetic field in a general way, partly because of the greater number of contours that could be shown at once in a plot. This 2D case is actually more helpful in my mind because the field of a single dipole is so symmetric in a lot of ways that 3D images actually just confuse the issue and get in the way of each other. If I got the chance to model multiple dipoles, I likely would have tried to keep their dipole moments (vectors normal to the center of the current loops) in the same plane (xz most likely, for consistency). This way, at least in some regions, the field would still be independent of $\phi$, and thus the analysis of such fields would be simpler.

The 3D graphical limitations of Mathematica could be seen on some of my contour plots, especially those with the current loop shown as well, where the surface disappeared around the xy plane. I expect this is due to the near horizontal nature of the contour at this point, and the rendering issues that come into play when plotting such an extreme surface. The limitations (or just my inability to utilize Mathematica to its full extent) of VectorPlot3D and similar functions are pretty obvious in my case as they didn’t work well at all for the vector functions that I was trying to plot.

Despite these limitations and my Mathematica difficulties, I think that I managed to convey a good amount of information about the fields (and the less generally useful equipotential surfaces) of a single magnetic dipole. Hopefully I also laid the groundwork for students in this class in the future to work on modeling magnetic dipoles, specifically multiple dipoles in complex configurations. I also learned a lot about the benefits, frustrations, and limitations that Mathematica brings to the table as a computational scientific tool.

Conclusion: Corrections and Deconvolution

Update:

I concluded in my preliminary data post that the ‘Convolve’ function has its limitations and will not work properly with complicated functions. That may be so with relatively obscure functions, but I was wrong in my example. When I computed the convolution the long way by taking the Fourier transform of the product of Fourier transforms, I used the ‘FourierTransform’ function. I should have used the ‘InverseFourierTransform’ function instead. A Fourier transform of a Fourier transform is not necessarily the same as the inverse Fourier transform of a Fourier transform.

If $f_1(x)=exp(-x)unitstep(x) \quad f_2(x)=cos(x)$ , then through both methods I yield this plot:

Mathematica file: https://vspace.vassar.edu/zerogoszinski/Update.nb

Vspace works better on Macs. If you are not using a Mac, please open the file from the Google Drive folder located at the end of this post. The file name is called ‘Update’.

Deconvolution:

Convolution has applications in imaging, in that a blurry image is simply the convolution of the image and a lens or instrumental function. This function is also called ‘point-spread function’ (PSF). Convoluting two functions is simple since the individual functions are known. Deconvolution is the reverse process, in which you have a convolution and you want to extract the desired image. This requires an understanding of the blurring function, which requires understanding the system that is causing the distortion. Extracting the pure image is much more difficult since every blurring variable needs to be taken into account. A perfect PSF is impossible to determine, so accounting for this function requires good approximations (4). Deconvolution is very important in astronomy, since all data comes from optical based systems. Even a perfect lens convolutes images, as they have unique diffraction patterns. The best focused spot for a camera lens is called the Airy disk:

$\theta=1.22f\lambda/d$

f is the focal length, $\lambda$ is the wavelength, and d is the diameter of the lens.

http://upload.wikimedia.org/wikipedia/commons/thumb/4/4b/Airy_disk_created_by_laser_beam_through_pinhole.jpg/480px-Airy_disk_created_by_laser_beam_through_pinhole.jpg

Here is an example of deconvolution in action:

http://opticalengineering.spiedigitallibrary.org/article.aspx?articleid=1183218

“Experience with the Hubble Space Telescope: 20 years of an archetype”
http://opticalengineering.spiedigitallibrary.org/article.aspx?articleid=1183218

A particularly cool example of the effects of PSF in astronomy is the black-drop effect during the transit of Venus. The black-drop effect is an optical effect where the planet seems to stick to the edges of the star during ingress and pull apart like taffy as it enters the surface. Calculating the transit time would determine the orbital period of Venus. Kepler’s third law would then determine the radius of orbit. Astronomers of the 18th and 19th century wanted to figure this out in order to determine the actual size of the solar system. The black drop effect made it difficult to determine the exact moment Venus entered the Sun’s surface. The cause for this effect was discovered to be mostly due to PSF (Schneider, G., Pasachoff, J. M., Golub, L., 2004, Icarus, 168, 249). Poor optics creates this optical illusion, and accounting for point-spread function [and solar limb darkening] eliminates this effect.

Click to see the animation.
Created by Zeeve Rogoszinski using data taken from Big Bear Solar Observatory.
http://imgur.com/p19moKI

As you can see convolution and deconvolution have important applications in optics. Light beams get distorted as they pass through matter, and the scientist needs to be able to determine what exactly he or she is looking at. If I had the time I would have tried to deconvolute my convolution in the previous post, and try to extract one of the optical filters. I would have first assumed I knew what the second filter looked like, and try to work out the procedure from there. I would then assume I have no idea how the filters behave, and try to blindly deconvolute the filters. This would require looking into the theory behind deconvolution in a more rigorous manner.

Transit Paper:

http://web.williams.edu/Astronomy/eclipse/transits/Schneider_jmp_lg_Icarus2004.pdf

All of my data:

https://drive.google.com/folderview?id=0BxRRP3LUVuftVmFCcnNPMWFhU1k&usp=sharing

Final Data

The next phase of my project involved actually creating some models of the magnetic field of a magnetic dipole. This proved to require more steps and creativity than previously thought, but in the end I did get some useful plots. The three finalized Mathematica files that I refer to throughout this post can be found via the link at the bottom of this post.

The first breakthrough I had was using a different technique to convert the expression for the magnetic field from spherical to cartesian coordinates so that Mathematica can plot some version of its information. This technique worked way better than using Mathematica’s built in TransformedField function, which produced some weird results (see Preliminary Data post). Instead, I decided, with the help of Shelly Johnson, to write out the explicit cartesian forms of $r$, $\theta$, and $\phi$ as well as the explicit spherical forms of $\hat{r}$ $\hat{\theta}$, and $\hat{\phi}$, and then let Mathematica substitute these expressions in the larger expression for the magnetic field. This worked pretty well to give the three components of the magnetic field, $\vec{B_x}$, $\vec{B_y}$, and $\vec{B_z}$, as can be seen at the top of my Mathematica file titled “3D_vector_graphs.nb”.

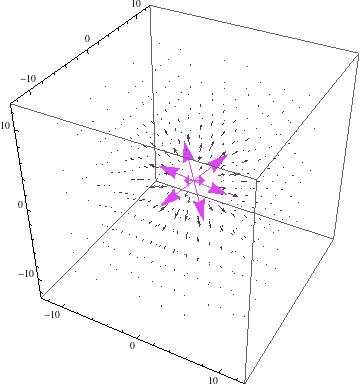
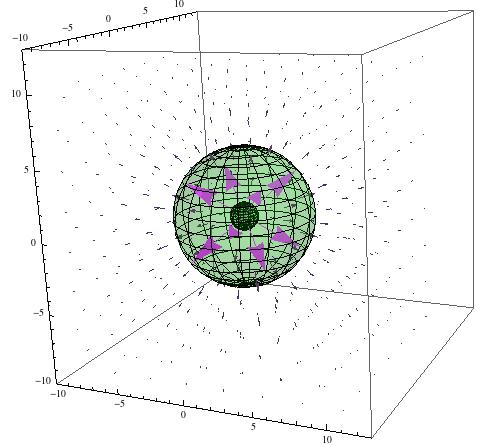
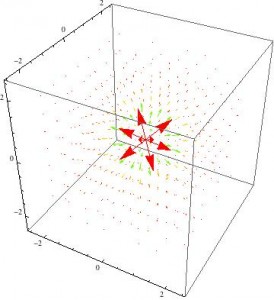
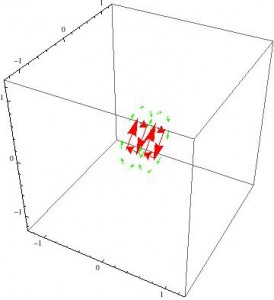
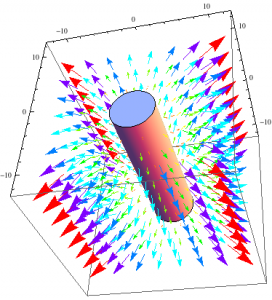
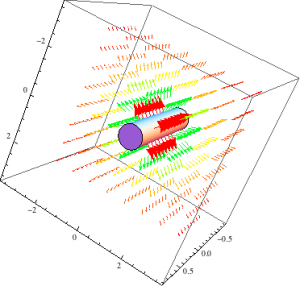
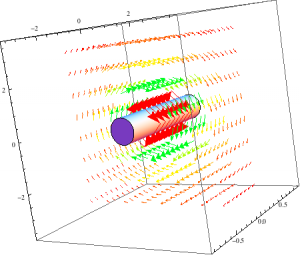
When these expressions are plotted using VectorPlot3D, however, the results are pretty uninformative.

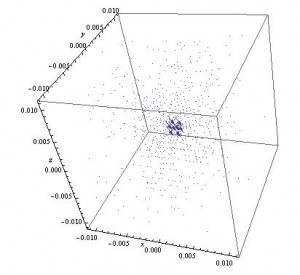
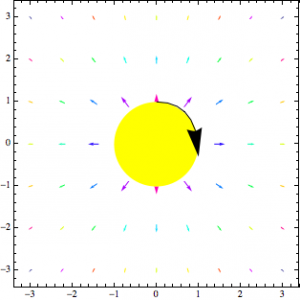
3D vector plot of the magnetic field of a magnetic dipole

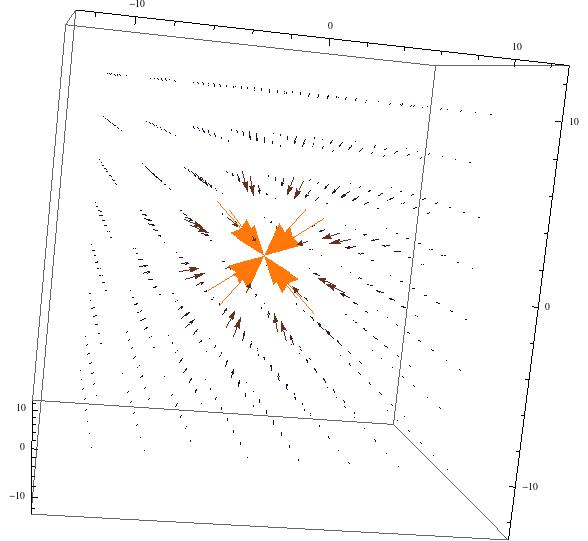
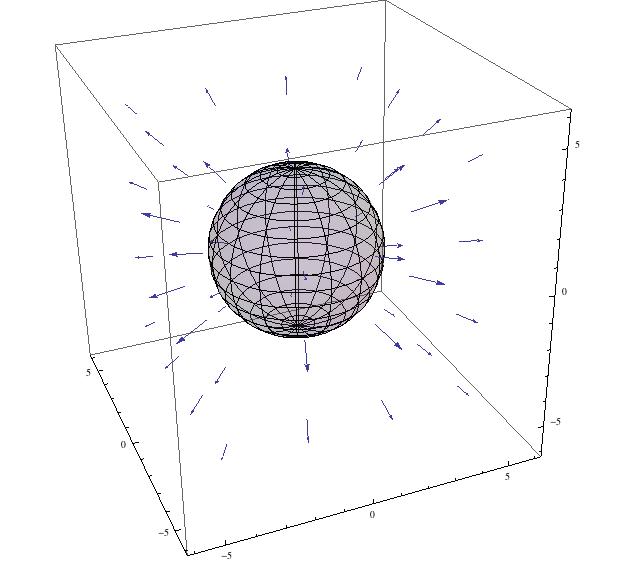
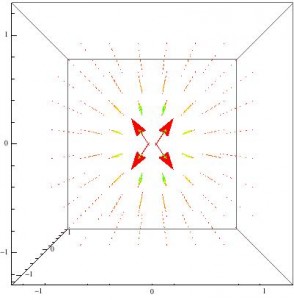
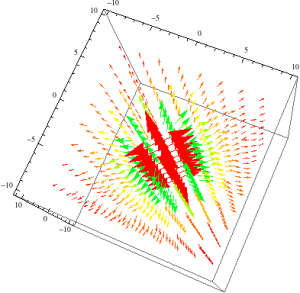
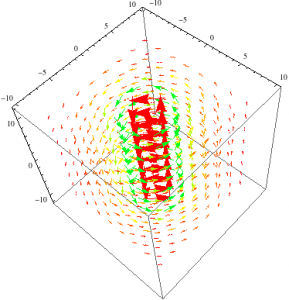
Even zoomed in and seen from a more right angle, this field is not helpful.

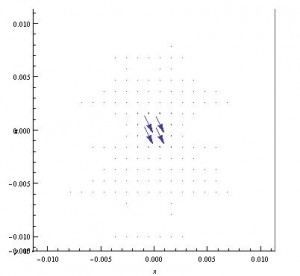
Same plot as above, but seen zoomed in and in the xz plane

Since this approach didn’t work well, for reasons discussed more in my next Conclusion post, and my previous attempts at plotting the vector field at representative points was getting complicated as well, I decided to try to use this new transformation by substitution method to try Contour plots instead.

I began by forming one expression for the magnetic field value at points in space, with no vector information. This expression ends up being pretty manageable, and the contours of this can be made effectively using ContourPlot3D. Some different results are shown below, taken from my Mathematica file “3D_contour_graphs”.

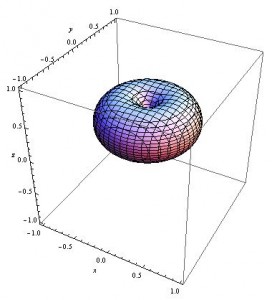
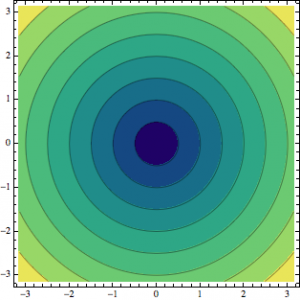
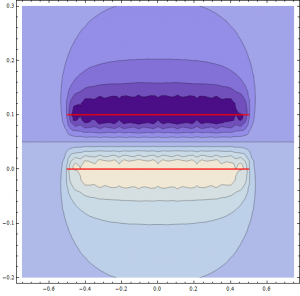
3D contour of my expression for the magnitude of the magnetic field of a magnetic dipole. This contour is for when the magnetic field equals 1

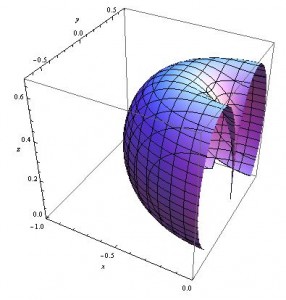
The same plot as above, but this time zoomed in and shown “cut in half” to see what happens on the inside of the symmetric circular outer portion

These results are pretty promising, so I then added in a few more contours, to see how the different values looked relative to one another.

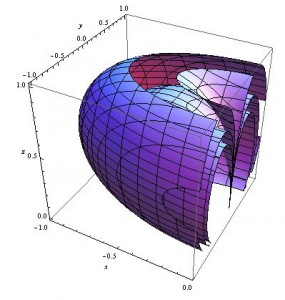
Similar plot to the above, but this time with three contours. From the inner to outer contours, these surfaces represent the places where the magnitude of the magnetic field equals 0.75, 0.5, and 0.28 respectively.

This is pretty good, but where are these surfaces in relation to the small current loop that is supposed to be creating these magnetic field contours? My next few contours include a small yellow ring at the origin, which indicates the placement of the loop, and also plots both positive and negative contours, which gives the whole picture both above and below the ring (which, looking at the original equation, should be symmetric).

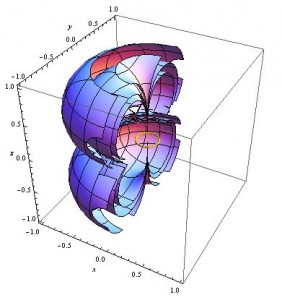
The same three contours as above, along with their negative counterparts, and a small yellow ring representing the current loop that creates the magnetic field modeled.

A different view of the above graph, which allows one to look into the part of the contour that has been “cut open”.

Now that there is a current loop in our models, what happens when the current in this loop is increased? The above models were made with a magnetic dipole moment, $m=1$, but the below image increased the current so that $m=2$.

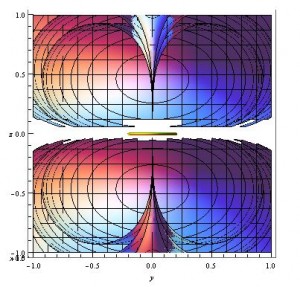
Similar plot to above, but with a stronger magnetic field (m=2).

Putting images with $m=1$, $m=2$, and $m=3$ side by side shows that the same contours move farther away (and change curvature a bit) for models with larger m values, which is expected because larger m values indicate larger magnetic fields.

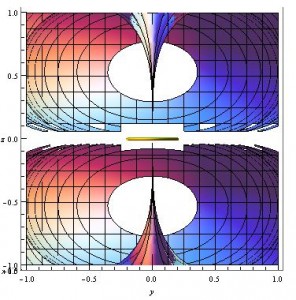
From left to right, Contours with m = 1, m = 2, and m = 3.

This is all pretty good, but what are these contour surfaces actually telling us about the magnetic field? These contour surfaces represent places where the magnitude of the magnetic field is at a constant value, so these shapes represent equipotential surfaces. While equipotential surfaces are not often talked about when talking about magnetic fields, the general principle that field vectors are perpendicular to equipotential surfaces is true of magnetic fields as well as electric. Therefore, these contours actually tell us something about the magnetic field of a dipole, albeit in an indirect manner.

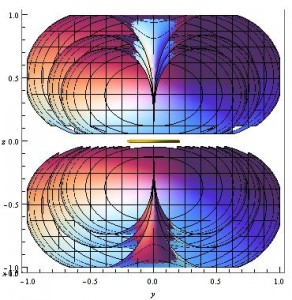
To try and get a better picture of what the field lines look like around this current loop, I plotted these contour surfaces in 2D by removing any y dependence, so that the 2D contours plotted are shown in the xz plane. This doesn’t lose much information again because of the $\phi$ independence of the magnetic field of a dipole. The result is shown below, which is taken from my Mathematica file “2D_contour_graphs”.

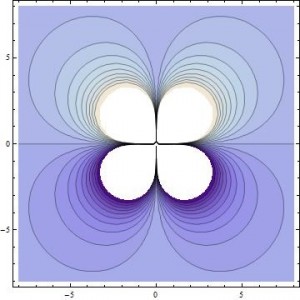
2D contour, showing 20 different contour lines, both positive and negative.

This gives us a representation where the vector field lines may be easier to picture, and easier to compare to the lines shown in Griffiths’ “Introduction to Electrodynamics” 5.4.3 – pg. 255, which are shown in 2D. It took some squinting, but I can see that lines perpendicular to these (and more) contour lines forms loops expected of a magnetic dipole. I overlaid a few representative loops over my 2D contour image in paint to illustrate this idea.

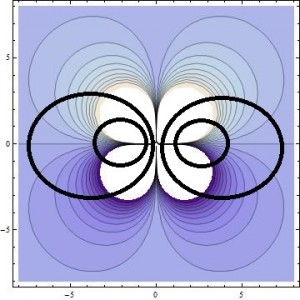
Same image as above, but with (approximate) magnetic field lines overlaid in thick black.

Link to final Mathematica files: 3 Final Mathematica Files

Railgun Physics: Final Thoughts

Having completed this project I have several thoughts about what I did, what I could’ve done, and what I want to do in the future. This project taught me a lot about physics, a little about engineering, and a great deal about modeling and the work and mindset necessary to complete projects of this nature.

The physics I got to explore as part of this project was extraordinary. Before I began, I knew little about railguns, only that they used extremely powerful electromagnetic forces to create massive destruction. The first part of my results showed an interesting but unsurprising result. The initial current originating from the capacitor was extremely large; a capacitor charged to 1.8 coulombs generated an initial current of over a million amperes. At first, this value seemed a bit high, and in reality was most likely a little higher than we expected. However, within a matter of several hundredths of a micro-second, this value immediately dropped to several hundred thousand amperes and then even lower values shortly thereafter. The current dropped even further when the length of the rails changed or when the cross sectional area of the rail decreased. Doing both of these, something that is realistic over time, lowers the current even more drastically. Therefore, we saw that the rail gun really does involve an initial intense burst of current followed by no further circuit action. We then saw the effect of EMF. At the beginning of the project, I thought that EMF would be too hard to derive and almost discounted it. Having done it, I realize that this decision would have been poor, as EMF ended up playing a huge role. The EMF induced a current that reduced the original current by almost 3/7ths, a substantial amount. Once again, this factor was dependent on the length of the rails and conductivity of the material. Finally, the resulting magnetic field was extremely powerful but fell in line with all the other results we found. In the first moments of the circuit’s operation, an enormous magnetic field is generated, creating a large force for a very brief amount of time. This occurrence made sense of course, as magnetic field depends on current. I am happy with these results, as they mirror the conceptual understanding of railguns I have developed during the course of this project; an enormous power lasts for an infinitesimal amount of time.

Part of our project was not able to happen, of course. We had originally planned to build the small scale rail gun, but because of time and safety concerns were unable to. In the future when doing these kinds of projects I will be able to better adjust my plans for safety and for time. I also could have tried to make more 3D models of my models, but thought that the 2D representations made sense in the context of the project.

In the future I would like to be able to derive equations of motion as functions of time. So many of the results I obtained were dependent on velocity and position. I adjusted for this by allowing these variables to be selected over a certain range; for example, using my model can tell you what the magnetic field of a railgun is at an exact time, position, and velocity. This result is very useful, but I would ideally like to be able to have position and velocity as functions of time as well. With more time and more math, specifically a greater knowledge of differential equations, I think I would be able to do so.

Conclusion: Diffraction Patterns of C. elegans

I set out to model the diffraction patterns created by C. elegans nematodes using mathematica, specifically using the diversely useful mathematical tool of the Discrete Fourier Transform. The Transform is a quick way to find the diffraction patterns from Fraunhofer diffraction and interference (far-field diffraction). In simpler language, $\left| FT^{2} \right|$ produces the diffraction pattern, which is an analysis of the Electric field strength across the aperture, in this case, the image. The goal of this project was to produce a “library” of shapes and their corresponding diffraction patterns. However, there were many obstacles that made it necessary for me to do quite a bit of relevant research.

When I started, I did not know that the type of diffraction I was studying was Fraunhofer. Diffraction patterns are a result of the type of wave and the type of experimental setup. In this case, the light source, the aperture, and the screen were are far enough away to classify it as far-field. Mathematically, $L>>\frac{b^{2}}{\lambda}=\frac{area. of. aperture}{\lambda}$ . The fact that this is an example of Fraunhofer Diffraction makes it possible to apply the FT (on Mathematica) to yield the diffraction pattern.

I came in with some preliminary knowledge of what Fourier Transforms were in theory. In general, when applied, it changes a function’s variable dependence: $F(t) \leftrightarrow \Phi (v)$. I did quite a bit of research on the derivations of the transform and understood the matrix calculations necessary to do the transform “by hand” (see Project Plan).

To produce good-quality images, it was also necessary to do quite a bit of exploring in the Mathematica Documentation Center, becoming familiar with a variety of image manipulation commands. Those included: sharpening, brightening, finding the pixel count and dimensions, cropping, changing the color scheme to grayscale, partitioning and reassembling images manually based on the pixel dimensions, and more, depending on what degree of manipulation the image needed.

All in all, the images produced are not only pretty, but informative and now available for reference. Because it is mathematically impossible to go from the diffraction image to the shape, it is necessary to have some type of library, like the one I created, to go in that direction. (It is impossible to do it mathematically because when the Fourier Transform is applied, the phase information of the light is lost as the data is converted to the complex space.) Therefore, my “library” is useful because I have made it possible to guess the approximate shape and orientation of the worm from the diffraction pattern for some basic worm shapes. Another application for this analysis is that a compilation of several consecutive diffraction patterns shows the thrashing frequency of the worm. For example, if you took several pictures within a few seconds and found the diffraction patterns, the amount that the patterns change corresponds to the “thrashing frequency,” or the quantifiable amount that the worm wiggles.

If I were to continue this project, I would continue to build upon the library in the same manner, testing to see if different input image qualities would make a difference in the final product (if different pieces of the worms were fluorescing, if the worm was glowing a different color, etc). Finally, I would construct a real library (instead of this evolving blog site) that was easy to navigate, and generally more accessible for research.

Conclusion- RLC Circuits

Overview

In this post, I will draw conclusions from my previous final data post about both RLC circuits that I have modeled.

RLC Circuit- No Voltage Source

This RLC circuit [Figure 1] proved to be an interesting demonstration of the current in a circuit without a voltage source. The initial current running through the circuit is provided by the charged capacitor. However, this initial current undergoes damping due to the resistor in place, and the current running through the circuit pretty approaches zero pretty quickly.

[Figure 1]

My model of this circuit verifies this idea since it shows an exponential decay of the current as a function of time [Figure 2]. After about 4 seconds, there is no longer an active current running through the circuit due to the resistor. My Mathematica notebook is easily set up for changing the values of the different components, and one can easily change them to see what effect this has on the circuit.

[Figure 2]

RLC Circuit- AC Voltage Source

The second RLC Circuit that I modeled was identical to the one above, except that it had an alternating current voltage source as well [Figure 3]. This allowed it to continue to have a current present despite the effects of the resistor.

[Figure 3]

Initially, I approximated the solution to the differential equation governing the circuit by ignoring the damping terms. This resulted in a an extremely good approximation, as the damping terms should only effect the circuit’s current flow in its first few seconds. After some computational hiccups that inaccurately displayed long-term variations in the current, I went on to graphically solve the complete form of the equation and graphed it to prove that the two damping terms only had a small effect in the first few seconds of the circuits behavior[Figure 4].

[Figure 4]

Final Remarks

Given the chance to work more on this project, I would develop manipulable animations within Mathematica that would allow one to change a given variable (ex. resistance, inductance, capacitance). This would allow the reader to easily see the effects that the different components have on the circuit. This would also be helpful from an educational standpoint as an applet to someone wanting to learn more about RLC circuits, or circuitry in general.

On a final note, I managed to learn a lot more about Mathematica and its differential equation solving capabilities. Solving the equations for these circuits by hand would have been an extremely length procedure, but once I provided Mathematica with the commands in the correct syntax, it solved them much faster than any human could. This project helped me appreciate the uses of computational tools in physics, and I am very glad that they exist.

Final Data – E Fields of Spherical Objects

I began by modeling the electric field for a point charge +q, equal to the value of an elementary charge.

I also modeled the electric field of a point charge of -q.

Next, I attempted to model the electric field due to spherical hollow conductor with total charge +q. First, I graphed a sphere of radius 5 using Mathematica’s SphericalPlot3D function. I superimposed the electric field of a positive point charge over this sphere, knowing that this would be incorrect. By Gauss’s Law, the stated configuration would result in an electric field of 0 inside of the spherical conductor, and an electric field following $\textbf{E} = \frac{1}{4 \pi \epsilon_0} \frac{q}{r^2} \mathbf{\hat{r}} $ for r > 5. The following image shows a partially transparent sphere with an electric field inside of it, violating Gauss’s Law.

However, thanks to Brian Deer, I learned to use Mathematica’s RegionFunction, which allowed me to specify which regions of the graph on which the vector function would apply. The following now shows a hollow conductor of radius 3, with an electric field only present outside of it. Unfortunately, this step took a lot of time to work out, as I tried many different ideas to only get the field to show for certain radius values (i.e. be 0 inside of the conductor). I was unaware of RegionFunction, and even when I did learn what it was, I had trouble getting it to work with my model.

My updated Mathematica file can be found here.

Final Results: Modeling Relativistic E&M

The next step of my project involved applying the modeling and manipulation code to different scenarios. In this case, I chose two scenarios that started as purely electric and developed magnetic components when considered in moving reference frames. The first was a continuous case- an infinite parallel-plate capacitor, and the second was a discrete case- a single point charge.

As has been well established, the field between two capacitor plates of charge density +/-σ is E=σ/2ε0. It is unsurprising then, that the E-field of a capacitor looks like this:

It is equally unsurprising that since there is no moving charge, there is no B-field. Then, when the system is considered in a reference frame moving at speed v relative to the capacitor and the transformation equations are applied, the following fields emerge for E…

and B…

These look pretty dull, but are a few things to note about these figures. The first is that Mathematica is not able to show absolute magnitude of the vector fields: just the relative magnitude. That is, the arrows are the correct size relative to the other arrows in the box, but they are not necessarily to scale when compared to other fields. This is why the plots appear unchanged when v changes: the values of the vectors are all changing, but all at the same rate, so the pictures do not change.

The second notable feature is that (without accounting for the actual magnitudes of the fields), it is possible to see that even though the E- and B-fields both change, the direction of the net force does not. For a positive test charge at rest in the reference frame moving in the x-direction, it would experience only an electrostatic force in the z-direction in the rest case. For the moving case though, it would experience an E-field still in the z-direction and a B-field in the y-direction, both of which would result in a net force that is still in the z-direction.

Despite the simplicity of a point charge, this third case is actually the most interesting to look at because it is not infinite, but discrete. Thanks to every intro E&M course we’ve ever taken, we know that the E-field created by a test charge is E=q/r²4πε_0.The following vector plot or something similar probably appears in every intro textbook currently on the market.

Pretty boring, right? Completely spherically symmetric and falls off with r² as expected. Now for the interesting ones: the fields in a moving reference frame. The E-field actually starts losing gaining so much of a y- and z-component that it appears to flatten out in the x-direction. The following figure is for v=0.75c

The B-field does something equally strange: it becomes somewhat cylindrical. However, in my code, this only appears at very high v (greater than 0.96c).

I get the feeling that if I could make mathematica show more detail, the field would not be in a perfect cylinder though. Since two rings of vectors appear on either side of the origin, it may be that the actual field has two lobes of some sort that are symmetric about the x-axis.

The last thing to note about this model is that when v=c, the simulation returns an error because it has to divide by zero when calculating gamma. Furthermore, the expression for gamma returns imaginary numbers for v>c, so this model is not useful for considering hypothetically how a system might behave if anything were able to move faster than the speed of light.

The mathematica worksheet associated with this can be found here.

Final Models(Updated)

Magnetic Field for a Cylindrical Conductor:

LONG CYLINDER:

Using Ampere’s Law I derived the magnetic field for a simple system, a long cylinder with the current uniformly distributed on its surface. Using Eq. 2, I was able to solve for the magnetic field. The results are as follows:

A) For s < r, B=0

B) For s > r, $B=\frac{\mu _{0}I}{2\pi s}\hat{\phi }$ (1)

$\oint B\cdot dl=\mu _{0}I_{enc}$ (2)

In Figure 1 , we have a ContourPlot of the magnetic field of a long cylinder with a current I distributed on the surface of the cylinder. Assuming that the current is flowing into the screen we know that the magnetic field is in the positive ϕ direction. If the current were coming out towards us, the magnetic field would be in the negative phi direction.

Figure 1. This is a 2D contour plot that shows the flow of the B-field outside of the long cylinder. Look at this as if you were looking down on the cylinder with the current flowing into the screen.

Figure 2. Is another way of demonstrating what is happening to the long cylinder. This picture depicts the gradual decrease of the magnetic field’s magnitude as we move away further . The arrow curving around the top of the cylinder represents the direction of the B-field when the current is going into the screen.

Methods:

Using mathematica I was able to demonstrate these physical occurrences. Before developing the above figures I tried showing the magnetic field using the StreamPlot function, however that resulted in an oval like shape for the positive ϕ direction. The arrows are pointing in the right direction but the pattern formed does not represent the magnetic field for our situation. As you can see in Figure 3, the center of the plot starts of as a circle but as the radius of the cylinder increased the stream looses it’s circular shape and starts to flow like an ellipse.

Figure 3. This is a StreamPlot of the B-Field outside of the long cylinder. This is not a correct illustration of what is happening to the wire because it’s shaped like an ellipse.

Before entering my results into mathematica I changed from cylindrical coordinates to Cartesian coordinates using the TransformedField function. With this, my results are now

$B=\frac{\mu _{0}I}{2\pi \sqrt{x^{2}+y^{2}}} \widehat{\phi }$

Similar methods were used for the electric field.

Electric Field for a long cylinder:

Using Guass’ Law I derived the electric field inside of a long wire with charge density $\rho =ks$ , for some constant k. Using Equation 2, I got the equation $E_{inside}=\frac{ks^{2}}{3\epsilon _{0}} \widehat{s}$ .

$\oint E\cdot da=\frac{1}{\epsilon _{0}}Q_{enc}$ (2)

With this I modeled Figure 4, where the vectors point radially outwards of the cylinder. Figure 4, illustrates what happens in the center of the wire.

Figure 4. This is the Gaussian cylinder within an actual cylinder, where the magnitude of the E-field increases as the Gaussian cylinder approaches the size of the actual cylinder. Think of the axes as the parameters for the actual cylinder.

FINITE CYLINDER:

ELECTRIC FIELD FOR A FINITE CYLINDER:

After looking at the models for the long wire and talking to Professor Magnes about my blog I did modeling for an actual cylinder with parameters. For the E-field, the Cylinder is 30cm in length with a radius of 10cm. It has a charge density of $\rho =ks$ , which is the same as the long wire, only now confined to certain limits. After doing the math to find the E-field outside of the cylinder ( s > r ), I got

$\mathbf{E}=\frac{kl_{1}r^{3}}{sl_{2}\epsilon _{0}} \widehat{s}$ ,

where the k is a constant (where k = 1), $l_{1}$ is the length of the cylinder ( $l_{1}$ = 30cm), $l_{2}$ is the length of the Gaussian cylinder ( $l_{2}$ = 40cm), r is the radius of the Cylinder , and s is the radius of the Gaussian cylinder.

Figure 5. This is the E-field of a finite cylinder. As you can see here the magnitude of the E-field decreases the further you move away from the cylinder.

Figure 6. I placed the cylinder within the plain from Figure 5 to show the E-Field moving radially outward. I altered the size of the cylinder to have a better view of what’s going on.

MAGNETIC FIELD FOR A FINITE CYLINDER:

Here’s the magnetic field for a finite cylinder, with the same parameters as the one for the E-field. This is a cylinder with a current distributed uniformly across the surface of the cylinder. For this cylinder, I made the current (I) equal to 1A. After using Ampere’s law I got the same results as that of equation 1 from above.

Figure 7. The image on the left demonstrates the B-field of a cylinder. The image on the right shows the field on the left acting on a cylinder with set limits.

In this mathematica file you will also find a ContourPlot3D of what’s happening with the B-field. This file also contains the work I did for a Finite Cylinder.

To view the work I did in mathematica click on this link for the Electric Field:https://drive.google.com/file/d/0B2VxS7Y5dxIHMTZxUEFyb21yZWM/edit?usp=sharing

To view the work I did in mathematica click on this link for the Magnetic Field: https://drive.google.com/file/d/0B2VxS7Y5dxIHU0wxOTRHY0ZxdjA/edit?usp=sharing

Final Data: Capacitors

Abstract:

Using an approximation designed for this project, the energy storage capability as well as the capacitance of several simple, slightly physically impractical, square parallel plate capacitors were found. Compared to the idealized model taught in introductory physics, these capacitor store 90% to 97% the energy and have 94% to 98% the capacitance. These discrepancies are caused by the finite dimensions of the plates, which result in fringing effects at the edges. The accuracy of my model is likely high, based on a comparison of the approximations used and a sampling of values produced by the exact, theoretical model, which itself proved too computationally intensive to use extensively with the resources available. Overall, the discrepancies from the ideal model are fairly significant (a few percentage points) at the plate separations studied, indicating that this method could be quite useful for electronics applications. At closer, possibly more realistic plate separations, this relatively complicated model may prove too time consuming to justify its use over the ideal model, which represents the limit as separation approaches 0.

Methods:

Using Coulomb’s law for one particle $\vec{E}(\vec{r})=\frac{1}{4 \pi \epsilon_0}\frac{q}{r^2}\hat{r}$ , a massive grid of tens of thousands of points charges spread evenly across a predefined area could be constructed. The field of this grid was then compared at a few points to the field of the exact, theoretical values predicted by the more general (but not most general) form of Coulomb’s law:

$\vec{E}(\vec{r}) =\frac{1}{4 \pi \epsilon_0} \int \frac{\sigma\left(\vec{r'}\right)}{\mathfrak{r}^{2}}\hat{\mathfrak{r}} \: da'$ ,

or more explicitly:

$\vec{E}(x,y,z)=\frac{1}{4 \pi \epsilon_0}\int_{y'_i}^{y'_f}\int_{x'_i}^{x'_f}\sigma\frac{(x - x', y - y', z - z')}{((x - x')^2 + (y - y')^2 + (z - z')^2)^{3/2}}\mathrm{d}x'\mathrm{d}y'$

This was to determine how accurate the approximation was, though the exact method could not be used all the time as it was determined to be very computationally inefficient.

Plotting the electric field magnitude of a cross-section of the grid configuration like that described above, it is clear that the quantized nature of the grid disappears far away from it, but up close there are sharp irregularities (red lines represent the plates that are being modeled). Fringing effects can also be seen (note that a vector field proved too computationally intensive to plot). The configuration below is for a 14 by 14 grid for computational ease, much less fine that the 211 by 211 grids used in the simulations.

The field of a fine grid at thousands of locations within the capacitor was then calculated. From here, all parameters depending on E (the most important of which are energy storage, W, and capacitance, C) could be determined using:

$W=\frac{\epsilon_0}{2}\int E^2 (\vec{r}) \mathrm{d} \tau = \frac{1}{2}C V^2$

(Griffith’s 4^th Ed. eq. 2.45 and 2.55) where potential difference is V = Ed, an approximation from the ideal model used in the interest of time (though the E used was not the ideal values). Note that d = plate separation. Also note that the first equation was used in summation form $W=\frac{\epsilon_0}{2}\sum_{i} E^2 (\vec{r}_i) \Delta V _i$ (V here is volume) due to the quantization of the data (i.e. there was no easily integrable function for E).

Raw Data:

This project dealt with very large matrices (several were 3 by 1024) to examine the slightly variable electric field within a capacitor, and as such, much of that data is not of interest. The end results of these computations, however, are. The plates for all capacitors simulated were 4 square meters and had positive or negative 10^-6 Coulombs on them, with separation distance the only parameter being varied. Separation distances used were 0.01 meters, 0.015 meters, 0.02 meters, 0.025 meters, 0.03 meters, and 0.035 meters. Respectively, the energy that these capacitors stored in the space between the plates were (in milli-Joules): 0.137452, 0.202963, 0.266781, 0.328944, 0.38957, and 0.448766. Their respective capacitances were (in nano-Farads, a fairly typical capacitance unit (Griffiths 105)): 3.47951, 2.29386, 1.70372, 1.3506, 1.11583, and 0.948688.

Compared directly to the values predicted by the ideal model (namely that $W=\frac{\sigma^2}{2 \epsilon_0}Volume$ and $C=\frac{A \epsilon_0}{d}$ , A = area of one plate), the respective energy storage values are 97.36%, 95.84%, 94.49%, 93.20%, 91.98%, and 90.82%, while the respective capacitance values are 98.24%, 97.15%, 96.21%, 95.34%, 94.52%, and 93.75% (capacitance data is seen in the figure below).

So, while the values attained from both models are similar, the ideal model always overestimates the performance of the capacitor. To visualize the effect of plate separation on capacitor performance, below is an animation relating the two values. The separation is displayed above the left figure (green is the negative plate, blue is positive), while the straight line in the plot on the right is the energy storage as a function of time of the ideal capacitor. Data points are values from the model. Only a corner of the capacitor here is in view; if the whole object were displayed, the small separations would barely be noticeable:

References:

Griffiths, Electrodynamics 4th Ed.
Knight, Physics for Scientists and Engineers 2nd Ed
Servers through vapps.vassar.edu

Mathematica:

Core Folder (heavily commented, containing all necessary functions and graphics): https://www.dropbox.com/s/yk6omufo0sv4vlp/Final_ModelingCapacitors_Kachelein_PHYS341_2014.nb
Giant Data Folder: https://www.dropbox.com/s/tyyymcrwlo1oyex/Final_ModelingCapacitors_Kachelein_PHYS341_2014_GIANT%20DATA%20FOLDER.nb

Modeling and Experimental Tools with Prof. Magnes

Ideal for getting ideas and feedback on upper level physics tools.