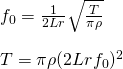Author Archives: lukachelein

Final Project Conclusions – Kachelein

Introduction

Each musical instrument has its own characteristic sound due to the contributions of different harmonic intervals above the fundamental frequency. The relative strengths of these harmonics are due to the mechanism of sound production and transmission of the instrument. For my project, I modeled the sound generation of two musical instruments, the harpsichord and clavichord. Building upon content in the class text (Giordano and Nakanishi, specifically chapters 6 and 11), I simulated the plucking action of the harpsichord for different values of several input parameters, compared computational results to data from a real instrument, and designed and executed a computational model for the clavichord.

Mathematical Background

For both instruments, the initial wavefronts evolved in time via

$\\y(i,n+1)=2[1-r^2]y(i,n)-y(i,n-1)+r^2 [y(i+1,n)+y(i-1,n)]$

where i is the spacial index of the wire’s height y, n is the temporal index, $r=c\Delta t/\Delta x = 1$ , Δx is the spacial step size, and Δt is the time step size. The parameter c is the speed of the wave on the string, and relied on several parameters of the string via

$c = \frac{1}{R}\sqrt{\frac{T}{\pi\rho}}$

where T is the tension on the string, R is the radius of the string, and ρ is the density of the string material. The final key equation needed is for the tension:

$T = \pi\rho(2 L R f_0)^2$

where L is the length of the string and $f_0$ is the fundamental frequency of the note desired. It should also be noted how to calculate the force of the string on the bridge (where sound is transmitted to the soundboard and then the air) using eq. 11.4:

$F_{\text{bridge}}=T\frac{y(2,n)-y(1,n)}{\Delta x}$

Harpsichord

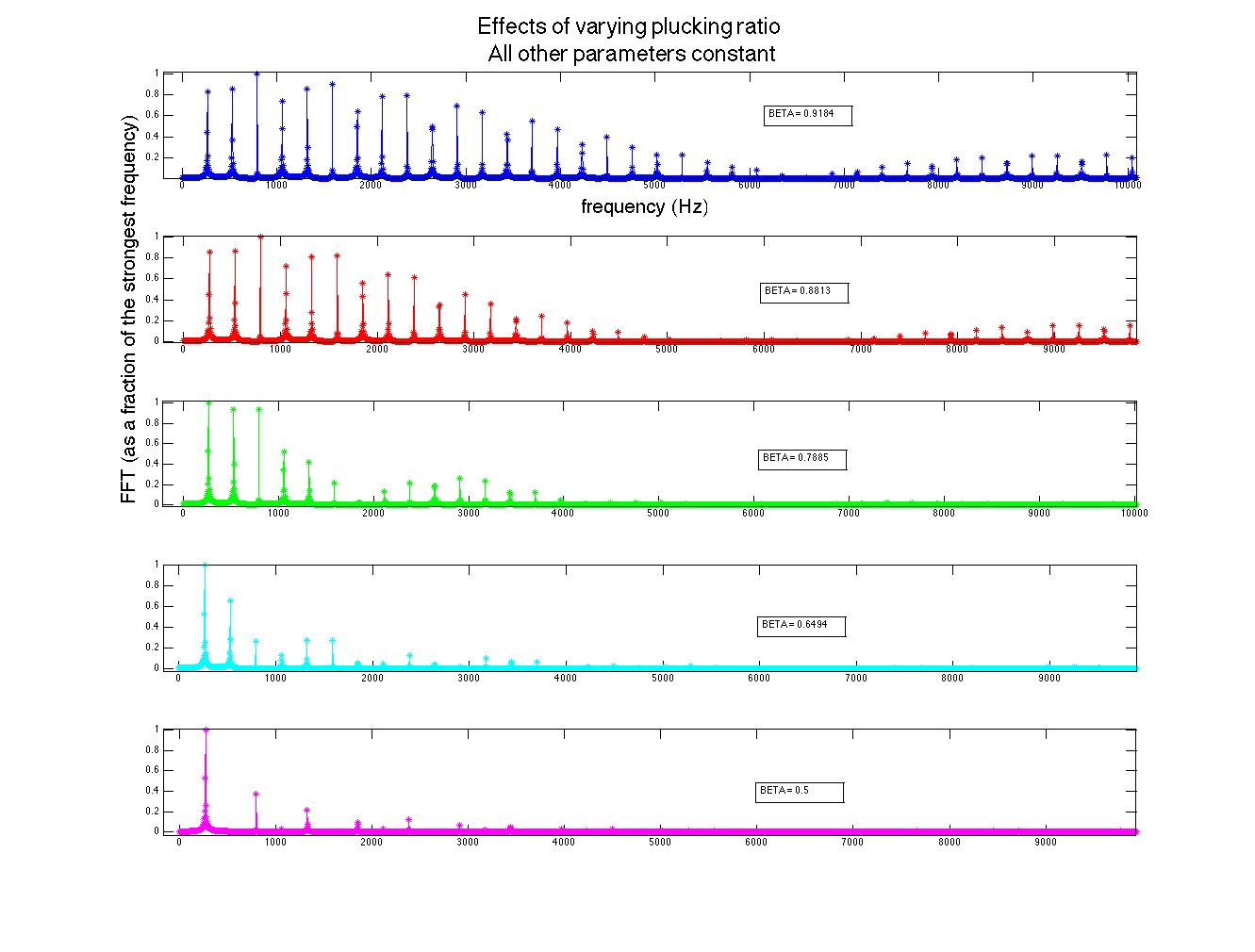
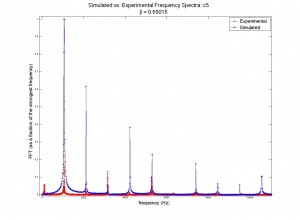
The computational model for the harpsichord was identical to that of a guitar; both are plucked string instruments that function in essentially the same way. Therefore, the initial wavefront was triangular. The plucking ratio β, a parameter used to set up the wavefront, proved to have the most effect on the frequencies generated (see figure 1). This can be explained by the formation of an antinode at the plucking point; if the string is plucked near its very edge, high frequencies will be present in the signal, as these frequencies result from standing waves on the string with much smaller wavelengths than the fundamental frequency. Because c is constant, these waves will have a high frequency contribution to the overall sound (recall that $f = \frac{c}{\lambda}$ ). Interestingly, the formation of an antinode at the plucking point prohibits frequencies that require a node at that point; for instance, a string plucked in the middle (β = 0.5) will only contain the fundamental frequency, the third harmonic, the fifth harmonic, etc., as seen in figure 1.

Figure 1 (click to expand): Variations in acoustic spectrum due to different plucking ratios. The strings here had a fundamental frequency of 261.63 Hz (middle c). Note that β > 0.5 simply means that the plucking point was not on the same half of the string as the bridge (sound transmission point). For instance, a plucking ratio of 0.75 is the same as one of 0.25 due to the symmetry of the string and has no bearing on the acoustic spectrum.

Changing other parameters (R, L, and plucking amplitude) had no effect on the relative strengths of the frequencies in the spectrum, assuming that all other independent variables were held constant. This may indicate a weakness in the model, as builders avoid deviating from tried-and-true ratios to avoid producing unpleasant sounds (as well as to avoid combinations of R and L that would require tensions that break strings).

The importance of β in producing a particular acoustic spectrum is evident in instrument construction. Harpsichords often have two plucking distances per note from which the player can choose, depending on the desired tonal effect.

After I developed a computational model, I compared results to recordings of individual notes from a real harpsichord. The .wav files used were part of a freely available sound bank of an instrument, designed to be used without intent for profit in musical instrument emulation software (Bricet & Garet 2007). Thus, the quality of the samples is high. Figure 2 compares the sound of the real instrument with that of the model; though the latter is clearly digitally generated, the sound produced is at least qualitatively similar to the physical system it models.

Figure 2: Qualitative comparison of actual data vs. model-generated data, link here (Youtube videos do not come through for all users).

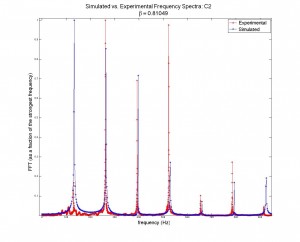
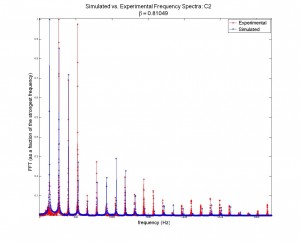
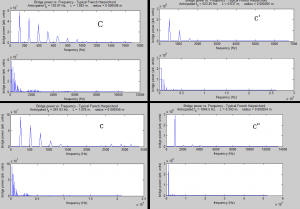
Quantitative analysis of the accuracy of the model vs. the physical data was not performed; this would have been essentially impossible without accurately knowing the plucking ratios built into the instrument that was recorded (there are no standards for β, which vary from one instrument to another and which are different note by note within the same instrument). However, I did plot generated acoustic spectra along side physical spectra in order to visually compare the model to the system (see figures 3 through 6). Though the relative strengths of the harmonic frequencies often mismatched, the model was very accurate in predicting which frequencies would be represented in a signal.

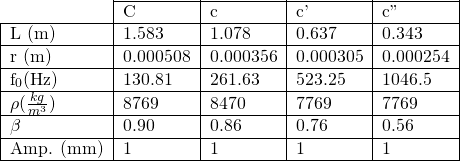
Figures 3 (at left) and (right): Model (blue) and physical data (red) acoustic spectra for the note one octave below middle c ( $f_0$ = 130.81 Hz). Figure 4 is simply a restriction of the data plotted in figure 3 to lower frequencies only. Some frequencies’ relative strengths matched well (e.g. second and third harmonics), while others were badly mismatched (e.g. first and fourth harmonics).

Figures 5 and 6: Similar to figures 3 and 4, but for the note two octaves above middle c ( $f_0$ = 1046.5 Hz).

Clavichord

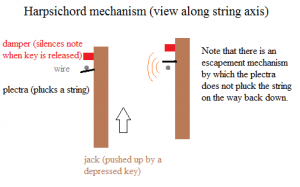
The mechanism of the clavichord is unique among musical instruments. Instead of hammering, plucking, or bowing a string, the string is struck at one end by a blunt metal point (via a piano-like key). The metal point, called a “tangent,” serves as one end of the sounding portion of the string; in effect, the player directly controls the boundary conditions of the system and can even slightly adjust the tension at will. Because there is no plucking point, a new computational model needed to be implemented.

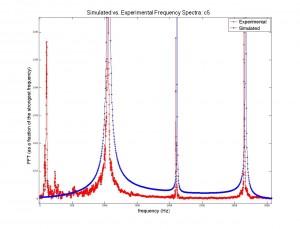
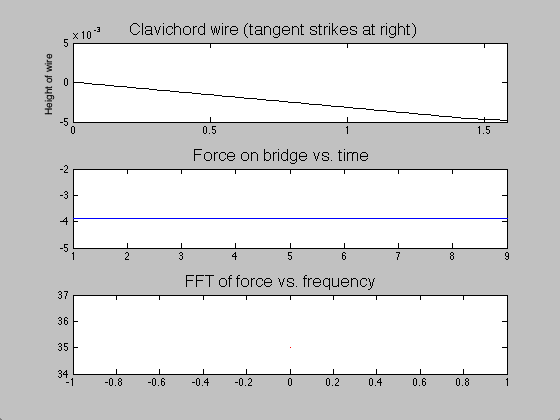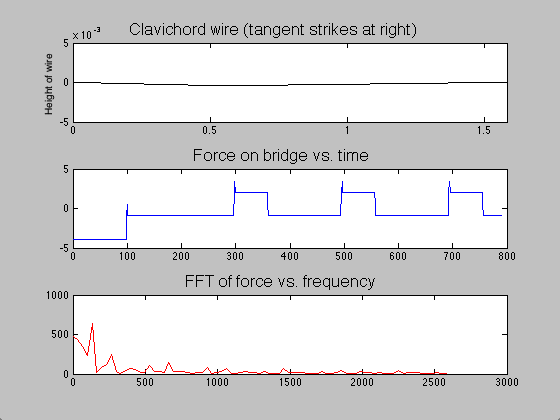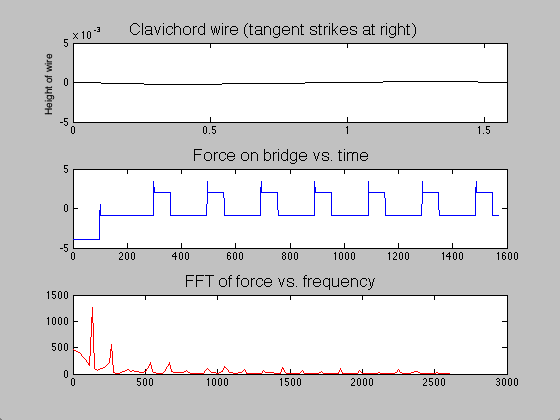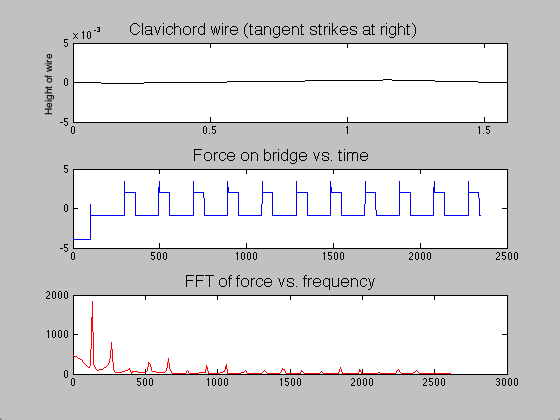
The difference between the clavichord and harpsichord required only a few changes in code. Instead of beginning the string as a triangle with a peak at the plucking point, the string began straight but with a negative slope. Upon running the program, one end of the string was raised over a length of time $t_{strike}$ ; when this time had passed, the moving end of the string became stationary, held in place for the remainder of the simulation. The time evolution of the string, the force on the bridge, and the Fourier transform (acoustic spectrum) of a note on the clavichord can be seen in figure 7.

Figure 7: Time evolution of clavichord string, bridge force, and acoustic spectrum.

Though acoustic spectra could be produced as they were for the harpsichord, these would not be illuminating, as I do not have audio recordings of individual clavichord notes with which to compare. However, due to the unrealistic sound that the model generates (not provided here), I suspect that the model, which is likely a good start, may be inadequate for several reasons. The fact that the model string starts stationary on the bridge end (see figure 7) requires many time steps to “even out.” Thus, low frequencies which are not part of the actual sound may be over-represented (note the initially strong contributions by f = 0 Hz). Second, all real clavichords have two strings per note, which may interact in subtle but significant ways that this simple model does not address. Finally, the tension in a real clavichord string changes slightly as the key is depressed, and that is not accounted for in this model.

Conclusions

Though there are issues with the models, especially the one I designed for the clavichord, all were successfully implemented and, with further refinements and more accurate input parameters (which are not possible without access to the instrument recorded), these models could be applied to instrument design. For instance, one could determine the optimal dimensions to achieve a desired tonal quality from an instrument.

In summary, I tested the validity of a given model against actual data, varied input parameters to determine effects on the model’s output, and derived a new model to describe a system that, at this early stage, seems to be reasonable if not somewhat simplistic. Beyond describing Baroque keyboard instruments, which I personally found to be an interesting topic, this project was a general exercise in research on a small scale. I started with a model or derived my own, implemented the model computationally, generated computational data, and compared the results to experimental data.

Code

https://www.dropbox.com/sh/paquzk0tml03k0j/AACz5zNErUctcIUKiJtFUesJa?dl=0

Ignore requests to sign up for a free Dropbox account; files can be downloaded without one.

Bibliography

Beebe, “Technical Library, Stringing III: Stringing Schedules“. Accessed 4/21/2015 at http://www.hpschd.nu/index.html?nav/nav-4.html&t/welcome.html&http://www.hpschd.nu/tech/str/sched.html (see “Hemsch Double”)

Bricet & Garet 2007, “Small Italian Harpsichord.” Accessed 5/11/15 at http://duphly.free.fr/en/italien.html

Claudio Di Veroli, “Taskin Harpsichord Scalings and Stringings Revisited“. Accessed 4/21/2015 at http://harps.braybaroque.ie/Taskin_stringing2.htm

Giordano N J, Nakanishi H. “Computational Physics, 2nd Edition.” 2005. Addison-Wesley. ISBN-10: 0131469908.

Malcolm Rose, “Wires for harpsichords, clavichords and fortepianos“. Accessed 4/20/2015 at http://www.malcolm-rose.com/Strings/strings.html

– MATLAB R2014b by MathWorks®

“Metals and Alloys – Densities“. The Engineering Toolbox. Accessed 4/20/2015 at http://www.engineeringtoolbox.com/metal-alloys-densities-d_50.html

“Vibrating String“. Georgia State University, Accessed 4/21/2015 at http://hyperphysics.phy-astr.gsu.edu/hbase/waves/string.html

Results and Data Analysis 1 – Kachelein

Instrument Background

This week’s work comprised of researching the various physical parameters needed as input for the model, which for the harpsichord is functioning properly. I initially believed that there might be a better way to describe the pluck wavefront on the string than simply two straight lines starting at zero at the edges at $y(\text{boundaries}) = 0$ and in the middle, at some midway point, at $y(\text{plucking point}) = \text{pluck amplitude}$ . However, this model, used in the book for the guitar, is physically accurate for the harpsichord as well, as both are plucked via a simple mechanism which, unlike the piano, does not impart a time-varying initial force, but rather a simple lift-and-release:

Figure 1: Diagram of the harpsichord’s plucking mechanism (own work).

I simulated the bridge power spectra of four notes from the range of a typical harpsichord: C, middle c, c’, and c”. However, the wire materials used in a typical instrument vary depending on the range of the note sounded; usually red brass is used in the lowest bass, yellow brass in the tenor range, and iron for the rest (Beebe). These different materials, naturally, have different densities, which play an important role in calculating the tension of the string (an input parameter that cannot be directly measured with any ease).

Calculating Tension

Begin with the equations for the fundamental frequency $f_0$ of a vibrating string (which defines the note sounded; the quality of the sound is dependent on the strength of specific higher harmonics that also sound):

$f_0 = \frac{1}{2 L}\sqrt{\frac{T L}{m}}$

where $L$ is string length, $T$ is tension, and $m$ is the total mass of the string (Vibrating String). More useful to us is the string’s volumetric mass density $\rho$ :

$\rho = \frac{m}{\text{Volume of wire}} = \frac{m}{L \pi r^2} \rightarrow \frac{L}{m} = \frac{1}{\pi\rho r^2}$

where $r$ is the (very small) radius of the wire. These equations can be combined to give:

$f_0 = \frac{1}{2 L r}\sqrt{\frac{T}{\pi\rho}} \\ \text{ } \\ T = \pi\rho(2 L r f_0)^2$

Armed with an expression for tension containing only known values, the simulations can be run. Note that length, density, and radii data can be found in the bibliography (Di Veroli)(Rose)(Metals and Alloys)(Beebe).

Results

Using the following parameters (some of which are from bibliography, cited above, while others were from personal measurement), the bridge force spectra were computed:

$\begin{tabular}{l|l|l|l|l|} \cline{2-5} & C & c & c' & c'' \\ \hline \multicolumn{1}{|l|}{L (m)} & 1.583 & 1.078 & 0.637 & 0.343 \\ \hline \multicolumn{1}{|l|}{r (m)} & 0.000508 & 0.000356 & 0.000305 & 0.000254 \\ \hline \multicolumn{1}{|l|}{f_0 (\text{Hz})} & 130.81 & 261.63 & 523.25 & 1046.5 \\ \hline \multicolumn{1}{|l|}{\rho (\frac{kg}{m^3})} & 8769 & 8470 & 7769 & 7769 \\ \hline \multicolumn{1}{|l|}{\beta} & 0.90 & 0.86 & 0.76 & 0.56 \\ \hline \multicolumn{1}{|l|}{Amp. (mm)} & 1 & 1 & 1 & 1 \\ \hline \end{tabular}$

Graphical representation of the fft’s of the four bridge force spectra computed (shown each at two different scales):

Figure 2: Force spectra for harpsichord strings given parameters above. Please click on image to view; any size other than full screen is illegible (hence why it is not full screen here).

Note that the waves in this model do not decay with time; this is a choice in the model and should not strongly effect the outcome, as the intention of the model is to simulate the harmonic frequencies immediately after the initial pluck, not the long term evolution of the system.

As the strings become shorter, the plucking point moves closer to the center of the string, changing the plucking ratio and altering the character of the sound, as indicated by a lack of abundant higher harmonics in the shorter strings (right two figures). This is in agreement with a qualitative understanding of the instrument; bass notes tend to have a more unique sound compared to the high notes.

Further, using the sound function in MATLAB to play back signals produces a very encouraging result: the sound generated purely by this computational model does, in fact, sound like a harpsichord. A further step of the project, analyzing data from the instrument itself, will tell whether or not the model is in quantitative agreement.

The next installment of this project will examine the clavichord, which has a method of sound generation almost unique among musical instruments, and hopefully will include analysis of actual harpsichord data.

Bibliography:

Claudio Di Veroli, “Taskin Harpsichord Scalings and Stringings Revisited“. Accessed 4/21/2015 at http://harps.braybaroque.ie/Taskin_stringing2.htm

Malcolm Rose, “Wires for harpsichords, clavichords and fortepianos“. Accessed 4/20/2015 at http://www.malcolm-rose.com/Strings/strings.html

“Metals and Alloys – Densities“. The Engineering Toolbox. Accessed 4/20/2015 at http://www.engineeringtoolbox.com/metal-alloys-densities-d_50.html

“Vibrating String“. Georgia State University, Accessed 4/21/2015 at http://hyperphysics.phy-astr.gsu.edu/hbase/waves/string.html

Code

https://www.dropbox.com/s/l8f3sscmel1qdko/Kachelein_Project_Results1.m?dl=0

Preliminary Results: Guitar Simulation – Kachelein

(Note that equations are rendered in LaTeX which I typed; they simply come through as images, though I include code for documentation.)

My preliminary results were fairly boring, in that I simply executed in MATLAB the guitar simulation central to the first part of chapter 11 of the text. However, this problem was not trivial, and the machinery constructed here will prove critical later in the project.

As background, recall in chapter 6 how the motion of a string was simulated using eq. 6.6:

$latex y(i,n+1)=2[1-r^2]y(i,n)-y(i,n-1)+r^2 [y(i+1,n)+y(i-1,n)]$

$\\y(i,n+1)=2[1-r^2]y(i,n)-y(i,n-1)+r^2 [y(i+1,n)+y(i-1,n)]$

where c = speed of wave and r = cΔt/Δx. The force on the bridge (defined here to be the left boundary of the string) can be calculated using eq. 11.4:

$latex F_{\text{bridge}}=T\frac{y(2,n)-y(1,n)}{\Delta x}$

$F_{\text{bridge}}=T\frac{y(2,n)-y(1,n)}{\Delta x}$

where T is tension, and y(1,n) is the leftmost element on the string at time n (this is a slight modification to the equation in the book, as MATLAB starts indexing at 1, whereas the book’s authors start at 0). For a string plucked at one fifth its length away from the bridge, the following results were obtained after simulating the vibrating string, calculating the force on the bridge with time, and taking the power spectrum of the force using the discrete Fourier transform written for class:

Prelim

Figure 1: Preliminary data. Bridge power spectrum calculated in MATLAB matches the results in the book very well, indicating that the code used is a good starting point for the rest of the project.

Code used attached here via DropBox (no need to sign up for an account).

Physics of Baroque Keyboard Instruments: Project Plan – Kachelein

Introduction

– In chapter 6 of the class text, we were first introduced to the motions of waves on strings, even modeling their motion in a few simple cases. In chapter 11, the physics of musical instruments is explored. The guitar and the piano are featured prominently in this chapter, as they have relatively simple mechanics and are stringed, hence the framework for exploring their behavior has been established. Other instruments, each with different physical characteristics, can also be modeled. The goal of my project is to start with information in chapter 11 and build full, working models of the harpsichord, clavichord and, hopefully, the pipe organ, three instruments with which I am very familiar. The final aim of the project is to compare computed data with actual signals from the instruments in question, verifying (or nullifying) the computational models.

Methods

– MATLAB will, of course, be used as the primary, if not sole, computational tool (if a difficult differential equation needs to be solved, Mathematica may be invoked). For the harpsichord, a model for the plucking force will need to be built (harpsichord strings are plucked, rather than struck like those of a piano). Though plucked strings are already discussed in the guitar sub-chapter, I feel that a more complicated but realistic model can be built (for example, by considering the effect of the plectra as the string slides off of it). The string’s motion will be governed, naturally, by the wave equation:

$\frac{\partial^2 y}{\partial t^2}=c^2\frac{\partial^2 y}{\partial x^2}$

which is computationally realized by eq. 6.6:

$\\y(i,n+1)=2[1-r^2]y(i,n)-y(i,n-1)+r^2 [y(i+1,n)+y(i-1,n)]\\\text{where }r=c\Delta t/\Delta x\text{ and }c\text{ is speed of sound in air.}$

– The clavichord is also a string instrument which has a striking mechanism like that of the piano, but which is physically much different. In particular, the forcing site is also a boundary of the string, so a radically different model from that of the piano/harpsichord may or may not need to be used.

– If the organ proves feasible after addressing the instruments above, I will attempt to model at least one type of pipe and at most two types (round metal and square wooden pipes). Part of chapter 11 addresses a one dimensional pipe, and the methods are claimed to be easily extendable to three dimensions using coupled partial differential equations. For the one dimensional case, we have pressure, p, and velocity, v, in air of density ρ and sound speed c given by:

$\\ \rho\frac{\partial v}{\partial t} = -\frac{\partial p}{\partial x} \\ \frac{\partial p}{\partial t}\ \ = -\rho c^2\frac{\partial v}{\partial x}$

which has a numerical form given by equation 11.37 in the book:

$v\left(M-\frac{1}{2},n+\frac{1}{2}\right)=\frac{1}{1+\frac{Z\Delta t}{\rho\Delta x}}\left[\left(1-\frac{Z\Delta t}{\rho\Delta x} \right )v\left(M-\frac{1}{2},n-\frac{1}{2} \right )+\frac{2\Delta t}{\rho\Delta x}p(M-1,n) \right ]$

where Z is acoustic impedance, the correct value of which will be of particular importance (material dependent).

– The experimental portion of the project is not yet laid out. I may request assistance from Professor Bradley in taking and analyzing acoustic signals from the aforementioned instruments. Regardless, I intend to compare the Fourier transforms of actual signals to the computed transforms in order to see if the peak frequencies match.

Time Line

– Week 1: Practice by completing a few problems from chapter 11.

– Week 2: Build a working model for the harpsichord, as complete as the piano model in the book, and take data. Begin work on clavichord model.

– Week 3: Complete clavichord model. Begin organ model.

– Week 4: Complete organ model. Record real instruments to compare to models.

– Week 5: Compare experimental data to models. Allow time for write up and possible revision of models.

– Week 6: Further time, submit Wednesday.

Resources:

– Giordano N J, Nakanishi H. “Computational Physics, 2nd Edition.” 2005. Addison-Wesley. ISBN-10: 0131469908.

– MATLAB R2014b by MathWorks®

PHYS 375 – Project Proposal (Fall 2015)

My proposed project will address musical instrument modeling, namely for the instruments I play, the harpsichord and organ. Computational Physics, by Nicholas J. Giordano and Hisao Nakanishi, addresses the piano, among other instruments, in chapter 11, which will serve as a starting point for modeling other musical instruments that have their own unique physical characteristics. For example, the harpsichord plucks, rather than strikes, its strings, and modeling a more accurate plucking force along with other features of the instrument would form part of the project. Another example is the variety of sounds produced by the pipe organ due to different pipe materials and shapes. I intend to model at least one pipe type (more if the harpsichord part of the project proves too simple). In all cases, I intend to compare the “bridge force spectrum” (basically, the force waves of certain frequencies exert at the boundary) that I calculate to an actual signal from the instrument itself, which I will record and analyze. This will verify, or nullify, the models that I will build.

Conclusions: Capacitors

(Revised 5/7/14)

Initially, I intended to model capacitors of various shapes, including more realistic configurations like rolled-up plates or variable (i.e. adjustable) capacitors. Though these configurations were not ultimately simulated, the information gathered, looking only at square parallel plate capacitors, was illuminating, and the foundational programs I wrote could, with some manipulation, be extended to more complicated arrangements.

The method I ended up using, detailed extensively in the data post, was relatively efficient but still took a non-trivial amount of time (see below) to simulate the electric fields that dictate the properties of a capacitor. The size of grid I used (averaged over two grids: one with 211^2 = 44521 points, the other with 212^2 = 44944 points) was chosen so that the simulated electric fields were at least 99.9% accurate over the distances examined and so that the simulations took no more than 10 minutes each to run (6 plate simulations were run in total, resulting in an hour of pure computation; note that by taking advantage of plate symmetry, this was actually 1/4 the time one might have expected, as it took about 2.4 seconds to find the E-field at any point).

Accuracy of the method at calculating the E-field was checked at a few points against the computationally inefficient but presumably 100% accurate theoretical model, which is based on fundamental physics (integral Coulomb’s law). This method took up to 10 minutes to calculate the E-field at an arbitrary point near the capacitor, though it was much faster far away from the capacitor (where we are naturally not interested).

Splitting a shape into thousands of manageable quantized points charges (each producing a field in accordance with Coulomb’s law for point charges) proved to be an effective tool, even for the relative simple square plates studied here. This method could be expanded in the future to much more complicated surfaces or even volumes to accurately model the electric field of complex shapes that would otherwise be hopeless to analyze analytically. Of course, a real charged object is charged with a finite number of charge carriers, so this method is not physically unsound (on the other hand, a plate charged to 10^-6 C like mine would need 6.25 x 10^12 electrons spread over it rather than a mere 44,000)

It should be noted that I did not examine the effects of dielectrics placed between plates. Though this was originally planned, I omitted doing this not out of time constraints, but rather because it would not have proved particularly illuminating. Linear dielectrics (the only kind extensively analyzed in 341) have very straightforward effects on energy storage and capacitance, which do not seem to depend on capacitor dimensions. Equation 4.58 and an unlabeled equation on page 197 make this clear (Griffiths, 4th ed.):

$W=\frac{1}{2}\int \vec{D}\cdot \vec{E}\text{ } \mathrm{d}\tau,\text{ }\vec{D}=\epsilon \vec{E}$

$C=\epsilon C_{\text{vacuum}}$

Overall, this project was an excellent exercise in computation and matrix manipulation (the data for the electric field at a set of points above a plate was stored in a 3 by 1024 matrix, for example). It was also very useful for practicing using approximation methods based on fundamental physics to solve an otherwise complicated problem. In the end, the ideal model of a capacitor was shown to be insufficient for extremely accurate capacitor parameters at all but the closets plate separations. Of course, real capacitors have by their design very close plates to maximize capacitance, so the choice of method depends on one’s needs and situation.

Perhaps the most useful “next step” would be to take the data for more plate separations and fit a curve to the points, resulting in a function for capacitance or energy as a function of plate separation. Based on the few points I took (see the animation), such a function is approximately a straight line for very small separations (i.e. the ideal approximation) but diminishes with distance like a square root function.

The code used to run these simulations could be expanded upon to use for visualizing electric or potential fields, or for any other application where an arbitrarily complicated electric field (or possibly a gravitational field) needs to be modeled. I tried to keep a neat, albeit very lengthy, notebook file, though I could have labeled my graphics and the computation times more clearly (I used the Timing function on almost every computation, but the way Mathematica returns the timing value is not extremely conspicuous).

Final Data: Capacitors

Abstract:

Using an approximation designed for this project, the energy storage capability as well as the capacitance of several simple, slightly physically impractical, square parallel plate capacitors were found. Compared to the idealized model taught in introductory physics, these capacitor store 90% to 97% the energy and have 94% to 98% the capacitance. These discrepancies are caused by the finite dimensions of the plates, which result in fringing effects at the edges. The accuracy of my model is likely high, based on a comparison of the approximations used and a sampling of values produced by the exact, theoretical model, which itself proved too computationally intensive to use extensively with the resources available. Overall, the discrepancies from the ideal model are fairly significant (a few percentage points) at the plate separations studied, indicating that this method could be quite useful for electronics applications. At closer, possibly more realistic plate separations, this relatively complicated model may prove too time consuming to justify its use over the ideal model, which represents the limit as separation approaches 0.

Methods:

Using Coulomb’s law for one particle $\vec{E}(\vec{r})=\frac{1}{4 \pi \epsilon_0}\frac{q}{r^2}\hat{r}$ , a massive grid of tens of thousands of points charges spread evenly across a predefined area could be constructed. The field of this grid was then compared at a few points to the field of the exact, theoretical values predicted by the more general (but not most general) form of Coulomb’s law:

$\vec{E}(\vec{r}) =\frac{1}{4 \pi \epsilon_0} \int \frac{\sigma\left(\vec{r'}\right)}{\mathfrak{r}^{2}}\hat{\mathfrak{r}} \: da'$ ,

or more explicitly:

$\vec{E}(x,y,z)=\frac{1}{4 \pi \epsilon_0}\int_{y'_i}^{y'_f}\int_{x'_i}^{x'_f}\sigma\frac{(x - x', y - y', z - z')}{((x - x')^2 + (y - y')^2 + (z - z')^2)^{3/2}}\mathrm{d}x'\mathrm{d}y'$

This was to determine how accurate the approximation was, though the exact method could not be used all the time as it was determined to be very computationally inefficient.

Plotting the electric field magnitude of a cross-section of the grid configuration like that described above, it is clear that the quantized nature of the grid disappears far away from it, but up close there are sharp irregularities (red lines represent the plates that are being modeled). Fringing effects can also be seen (note that a vector field proved too computationally intensive to plot). The configuration below is for a 14 by 14 grid for computational ease, much less fine that the 211 by 211 grids used in the simulations.

The field of a fine grid at thousands of locations within the capacitor was then calculated. From here, all parameters depending on E (the most important of which are energy storage, W, and capacitance, C) could be determined using:

$W=\frac{\epsilon_0}{2}\int E^2 (\vec{r}) \mathrm{d} \tau = \frac{1}{2}C V^2$

(Griffith’s 4^th Ed. eq. 2.45 and 2.55) where potential difference is V = Ed, an approximation from the ideal model used in the interest of time (though the E used was not the ideal values). Note that d = plate separation. Also note that the first equation was used in summation form $W=\frac{\epsilon_0}{2}\sum_{i} E^2 (\vec{r}_i) \Delta V _i$ (V here is volume) due to the quantization of the data (i.e. there was no easily integrable function for E).

Raw Data:

This project dealt with very large matrices (several were 3 by 1024) to examine the slightly variable electric field within a capacitor, and as such, much of that data is not of interest. The end results of these computations, however, are. The plates for all capacitors simulated were 4 square meters and had positive or negative 10^-6 Coulombs on them, with separation distance the only parameter being varied. Separation distances used were 0.01 meters, 0.015 meters, 0.02 meters, 0.025 meters, 0.03 meters, and 0.035 meters. Respectively, the energy that these capacitors stored in the space between the plates were (in milli-Joules): 0.137452, 0.202963, 0.266781, 0.328944, 0.38957, and 0.448766. Their respective capacitances were (in nano-Farads, a fairly typical capacitance unit (Griffiths 105)): 3.47951, 2.29386, 1.70372, 1.3506, 1.11583, and 0.948688.

Compared directly to the values predicted by the ideal model (namely that $W=\frac{\sigma^2}{2 \epsilon_0}Volume$ and $C=\frac{A \epsilon_0}{d}$ , A = area of one plate), the respective energy storage values are 97.36%, 95.84%, 94.49%, 93.20%, 91.98%, and 90.82%, while the respective capacitance values are 98.24%, 97.15%, 96.21%, 95.34%, 94.52%, and 93.75% (capacitance data is seen in the figure below).

So, while the values attained from both models are similar, the ideal model always overestimates the performance of the capacitor. To visualize the effect of plate separation on capacitor performance, below is an animation relating the two values. The separation is displayed above the left figure (green is the negative plate, blue is positive), while the straight line in the plot on the right is the energy storage as a function of time of the ideal capacitor. Data points are values from the model. Only a corner of the capacitor here is in view; if the whole object were displayed, the small separations would barely be noticeable:

References:

Griffiths, Electrodynamics 4th Ed.
Knight, Physics for Scientists and Engineers 2nd Ed
Servers through vapps.vassar.edu

Mathematica:

Core Folder (heavily commented, containing all necessary functions and graphics): https://www.dropbox.com/s/yk6omufo0sv4vlp/Final_ModelingCapacitors_Kachelein_PHYS341_2014.nb
Giant Data Folder: https://www.dropbox.com/s/tyyymcrwlo1oyex/Final_ModelingCapacitors_Kachelein_PHYS341_2014_GIANT%20DATA%20FOLDER.nb

Preliminary Data: Capacitors

Summary of Progress up to this Point:

I have found the energy storage capability of a simple, slightly physically impractical, square parallel plate capacitor. Compared to the idealized model taught in introductory physics, this capacitor stores 94.34% the energy, the discrepancy likely caused by the finite dimensions of the plates. The accuracy of my model is likely high based on a comparison of the methods used and a sampling of values produced by the exact, theoretical model.

Details:

Recall Coulomb’s Law for a charged surface: $\vec{E}(\vec{r}) =\frac{1}{4 \pi \epsilon_0} \int \frac{\sigma\left(\vec{r'}\right)}{\mathfrak{r}^{2}}\hat{\mathfrak{r}} \: da'$ . In Cartesian coordinates for a flat plate lying in the xy-plane at z=0, this can be more explicitly written as:

$\vec{E}(x,y,z)=\frac{1}{4 \pi \epsilon_0}\int_{y'_i}^{y'_f}\int_{x'_i}^{x'_f}\sigma\frac{(x - x', y - y', z - z')}{((x - x')^2 + (y - y')^2 + (z - z')^2)^{3/2}}\mathrm{d}x'\mathrm{d}y'$

This complicated multi-variable vector integral expression is actually executed correctly by Mathematica, giving the field at a point very close to the middle of a rectangular charged plate, or of any point fairly far away from the plate in a short time (~10 seconds at the most on my personal computer). However, at points very close to the plate at an arbitrary location (for example, half-way between the center and a corner) the program took several minutes to evaluate; not a practical outcome. Therefore, my method of splitting the plane into thousands of tiny point charges (which is computationally efficient everywhere) needed to be examined for accuracy.

This method is built on the simpler form of Coulomb’s Law for a point charge: $\vec{E}(\vec{r})=\frac{1}{4 \pi \epsilon_0}\frac{q}{r^2}\hat{r}$ but is applied across thousands of point charges that form a grid superimposed over the plane being studied (the limit as the number of tiny charges approaches infinity is the exact expression). This method is extremely accurate at a distance, but up close it breaks down as the quantization of charge is noticeable, unfortunate given that capacitors are being studied. Therefore, the field produced by two slightly different arrangements was examined. For example, a grid of 100×100 points was calculated and averaged with a field produced by a 101×101 grid. This was done because a point that is very near a charge for one configuration is commensurable far away from the nearest charges for the other configuration. Averaging these out produces a value very close (only 0.04% too high) to the field of the theoretical model.

Once the model was justified, the points being tested were selected. Only points half-way between plates were evaluated because getting to close to the grid resulted in inaccurate values for the E-field, despite the otherwise successful attempt above to “smooth out” the point charges. Sampling this narrow range was justified because the exact method showed that the field varies by less than a percent across the small separation gap between plates. The values for the charge placed on the plates was taken from a problem in Knight.

To save time for the heavy computation, symmetry was invoked. Recognizing that only one quadrant of the area between plates needed to be evaluated, and that only one plate needed to be examined (because plates are identical aside from their charge sign), the computation was performed in one eighth the time previously expected. Nevertheless, the computation of the electric field at 256 points close to the plate took 10 minutes and 18 seconds when run through the relatively fast and efficient servers available to Vassar students through VApps.

To find the energy stored within, I had to reverse engineer eq. 2.45 (Griffiths, 4th Ed.). Instead of using the integral that describes the energy in a capacitor $W=\frac{\epsilon_0}{2}\int E^2 (\vec{r})\mathrm{d}\tau$ , I instead broke this integral into a sum:

$W=\frac{\epsilon_0}{2}\sum_{i}E^2 (\vec{r}_i)\Delta V$

where ΔV was the area in the immediate vicinity of the point sampled (for all 1024 of the evenly-spaced points, this was simply 1/1024 the total volume). This was necessary because I only have a quantized set of point at which I know the electric field, rather than an integrable function for the electric field.

In summary for the data gathered thus far, the energy stored in a 2 meter by 2 meter parallel plate capacitor with a separation of 2 centimeters is 0.2664 mJ. The basic approximation, where $\vec{E}_{ppc}=\frac{\sigma}{\epsilon_0}\hat{n}$ , resulted in 0.2824 mJ.

Next Steps:

As of yet, no visual aids have been developed due to the numerical nature of the early stages of the project. As the first heavy computation has been done and shown to be a success, time can now be devoted to the following:

Illustrating the fringing field at the very edge of a capacitor. This is likely one of the causes of the reduced energy storage observed compared to the infinite approximation, thus it would be an important concept to visualize.
Running a few more capacitor simulations and plotting the effect of plate separation on energy storage.

The math behind calculating related values (such as capacitance or the effect of an added dielectric) is fairly straightforward and can be saved until the end.

References:

Griffiths, Electrodynamics 4th Ed.
Knight, Physics for Scientists and Engineers 2nd Ed

Mathematica:

Main File: https://www.dropbox.com/s/2ab6445v9s95xvz/ModelingCapacitors_Kachelein_PHYS341_2014.nb
Data File: https://www.dropbox.com/s/47apmk39swj0ucn/ModelingCapacitors_Kachelein_PHYS341_2014_GIANT%20DATA%20FOLDER.nb

Project Plan: Capacitors

Goal:
Some features of real capacitors are sometimes ignored for pedagogical purposes, notably fringing fields. I intend to model a capacitor and its features, such as energy storage and capacitance, while making as few assumptions as possible, for example by paying attention to fringing effects (though assumptions, approximations, and numerical techniques will still be used as needed).

Methods and Comments:
Mathematica 9 will be used as the only computational tool to model a 3-dimensional capacitor. First, I intend to model the electric field of a rectangular conducting plate with uniform surface density σ. Then, using the principle of electric field superposition, I will find the combined field of this plate and that of an oppositely charged, geometrically identical plate offset by a small distance normal to the plane (i.e. a parallel plate capacitor). These fields will be based on Coulomb’s Law for a surface charge density:

$\vec{E}(\vec{r}) =\frac{1}{4 \pi \epsilon_0} \int \frac{\sigma\left(\vec{r'}\right)}{\mathfrak{r}^{2}}\hat{\mathfrak{r}} \: da'$

In addition, 3 approximations will be used: the simple capacitor field approximation $\vec{E}=\frac{\sigma}{\epsilon_0}$ to be quickly sure that the above results are correct, an electric field built using Mathematica’s NIntegrate function, which may be needed if the default Integrate fails to evaluate efficiently, and an approximation of my own design I call the “grid model,” whereby a charged sheet is replaced by a fine grid of hundreds or thousands of appropriately charged point charges. This may be necessary for oddly-shaped capacitors, and if it is sufficiently accurate, to “fill in the gaps” where other methods take too long and/or are inaccurate. Mathematica’s Timing function will be particularly useful for determining the efficiency of methods.
After the electric field computations have been done, the effects of a dielectric sandwiched between the plates can be analyzed using the principles of Griffiths, chapter 4. For example, once the electric field at a set of points in the capacitor has been found, one can, assuming linear dielectrics, apply $\vec{D}=\epsilon \vec{E}$ to find the electric displacement, and hence the energy stored in the configuration from the equation $W=\frac{1}{2}\int \vec{D} \cdot \vec{E} \: d\tau$ . This can be compared to stated values by capacitor manufacturers.

Preliminary Results:
My exact-value method based on Coulomb’s law works for a charged rectangular sheet in the xy-plane. At a point directly above the plate’s center at a distance reasonable for a capacitor (1% the width), the integral takes 9 seconds to evaluate; not unreasonable if time and ambition are budgeted. However, at a point half-way between the center and a corner, the program evaluated after 10 minutes, demonstrating the complexity of a seemingly simple integral. Using the grid method for a configuration of 40,000 point charges, however, yielded results that were 99.998% accurate in less than three seconds; the accuracy was barely lower for a 10,000 charge grid, which took half a second to evaluate. The grid method was also much more accurate than the infinite plane approximation taught in introductory physics, accounting for the finite dimensions of the sheet.

Time Line:
– Week 1: Further refine, test, and expand my existing models to work for more arbitrarily shaped plates.
– Week 2: Model the properties of simple parallel plate capacitors of rectangular and circular shapes.
– Week 3: Model the properties of more complicated capacitors, for example rolled up capacitors or variable capacitors.
– Week 4: Possibly account for more complicated properties of dielectrics, such as non-linearity. If this proves unmanageable, I may simply extend the work of week three.
– Week 5: Compare more thoroughly my models to real capacitors based on information from manufacturers and/or other sources. Also, this week, for which no computational work is budgeted, can be used as a safety net if previous weeks do not run as smoothly as I anticipate.

Collaborator(s): N/A

Resources:
– Griffiths “Introduction to Electrodynamics”, 4th Edition (this will be the primary source of information and equations that will be translated to Mathematica)

– Mathematica 9, Student Edition, including its extensive documentation.

– A relatively new edition of the “CRC Handbook of Chemistry and Physics” for values of the permittivities of different dielectric materials. Not yet procured.

– I am considering a resource on real capacitors, their energy storing capabilities, dimensions, and dielectric media to compare my values to the real objects I am modeling. However, at this early point in the project, this has not yet been procured nor will it likely be needed until week 3. Further, Griffiths has permittivity data, which may be sufficient.

– Through V-Apps, I may need to access more powerful computers than my 2011 laptop for intense computational work.

Project Proposal: Modeling Capacitors

I intend to model the capacitance, energy storage capabilities, and fringing fields of capacitors. The assumption of infinite area will be discarded in favor of using analytic approaches whenever possible; for example, one could start with Coulomb’s Law for a surface charge density:

$\vec{E}(\vec{r}) =\frac{1}{4 \pi \epsilon_0} \int \frac{\sigma\left(\vec{r'}\right)}{\mathfrak{r}^{2}}\hat{\mathfrak{r}} \: da'$

where $\vec{\mathfrak{r}}$ is the separation vector between a source point and the field point. From here, one can theoretically model the electric field of a sheet of arbitrary shape and charge density. I will start with a uniform charge density and a simply shaped sheet and work up to more complicated, realistic arrangements of positive and negative plates (i.e. capacitors, though not necessarily parallel plate capacitors only).

When a capacitor with a vacuum between the plates has been satisfactorily described, the effects of dielectrics placed between the plates could be modeled. Exotic dielectric media could be explored. If feasible, these realistic simulated capacitors could be incorporated into an RLC circuit model. As stated above, analytic solutions will be preferred, with approximations used only when the exact answer is computationally impractical. Approximations can, however, be used often as reality checks, as well as to compare the accuracy and computational requirements of approximations with those of the analytic solution.

Modeling and Experimental Tools with Prof. Magnes

Ideal for getting ideas and feedback on upper level physics tools.

Author Archives: lukachelein

Final Project Conclusions – Kachelein

Results and Data Analysis 1 – Kachelein

Preliminary Results: Guitar Simulation – Kachelein

Physics of Baroque Keyboard Instruments: Project Plan – Kachelein

PHYS 375 – Project Proposal (Fall 2015)

Conclusions: Capacitors

Final Data: Capacitors

Preliminary Data: Capacitors

Project Plan: Capacitors

Project Proposal: Modeling Capacitors