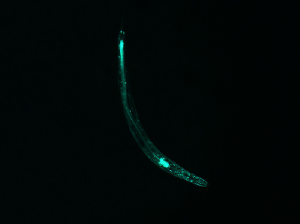
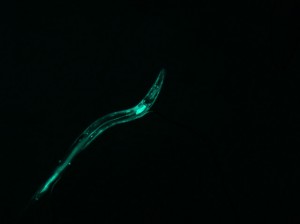
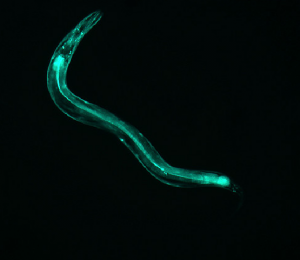
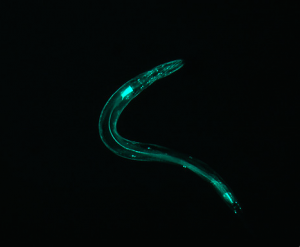
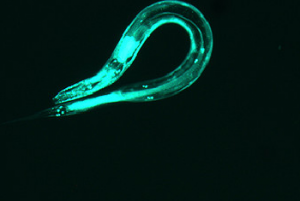
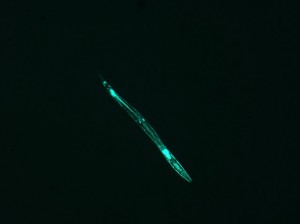
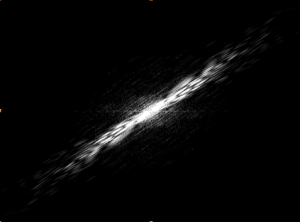
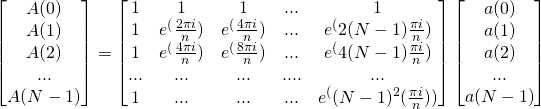I set out to model the diffraction patterns created by C. elegans nematodes using mathematica, specifically using the diversely useful mathematical tool of the Discrete Fourier Transform. The Transform is a quick way to find the diffraction patterns from Fraunhofer diffraction and interference (far-field diffraction). In simpler language, $\left| FT^{2} \right|$ produces the diffraction pattern, which is an analysis of the Electric field strength across the aperture, in this case, the image. The goal of this project was to produce a “library” of shapes and their corresponding diffraction patterns. However, there were many obstacles that made it necessary for me to do quite a bit of relevant research.
When I started, I did not know that the type of diffraction I was studying was Fraunhofer. Diffraction patterns are a result of the type of wave and the type of experimental setup. In this case, the light source, the aperture, and the screen were are far enough away to classify it as far-field. Mathematically, $L>>\frac{b^{2}}{\lambda}=\frac{area. of. aperture}{\lambda}$ . The fact that this is an example of Fraunhofer Diffraction makes it possible to apply the FT (on Mathematica) to yield the diffraction pattern.
I came in with some preliminary knowledge of what Fourier Transforms were in theory. In general, when applied, it changes a function’s variable dependence: $F(t) \leftrightarrow \Phi (v)$. I did quite a bit of research on the derivations of the transform and understood the matrix calculations necessary to do the transform “by hand” (see Project Plan).
To produce good-quality images, it was also necessary to do quite a bit of exploring in the Mathematica Documentation Center, becoming familiar with a variety of image manipulation commands. Those included: sharpening, brightening, finding the pixel count and dimensions, cropping, changing the color scheme to grayscale, partitioning and reassembling images manually based on the pixel dimensions, and more, depending on what degree of manipulation the image needed.
All in all, the images produced are not only pretty, but informative and now available for reference. Because it is mathematically impossible to go from the diffraction image to the shape, it is necessary to have some type of library, like the one I created, to go in that direction. (It is impossible to do it mathematically because when the Fourier Transform is applied, the phase information of the light is lost as the data is converted to the complex space.) Therefore, my “library” is useful because I have made it possible to guess the approximate shape and orientation of the worm from the diffraction pattern for some basic worm shapes. Another application for this analysis is that a compilation of several consecutive diffraction patterns shows the thrashing frequency of the worm. For example, if you took several pictures within a few seconds and found the diffraction patterns, the amount that the patterns change corresponds to the “thrashing frequency,” or the quantifiable amount that the worm wiggles.
If I were to continue this project, I would continue to build upon the library in the same manner, testing to see if different input image qualities would make a difference in the final product (if different pieces of the worms were fluorescing, if the worm was glowing a different color, etc). Finally, I would construct a real library (instead of this evolving blog site) that was easy to navigate, and generally more accessible for research.