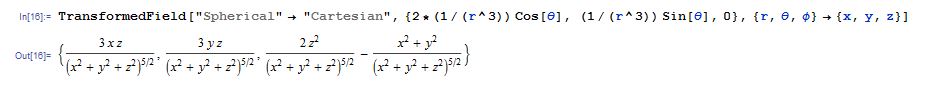Category Archives: Mathematica

Here is what Mathematica can do…

Van Allen Belt Modeling – Final Data

Background Information:

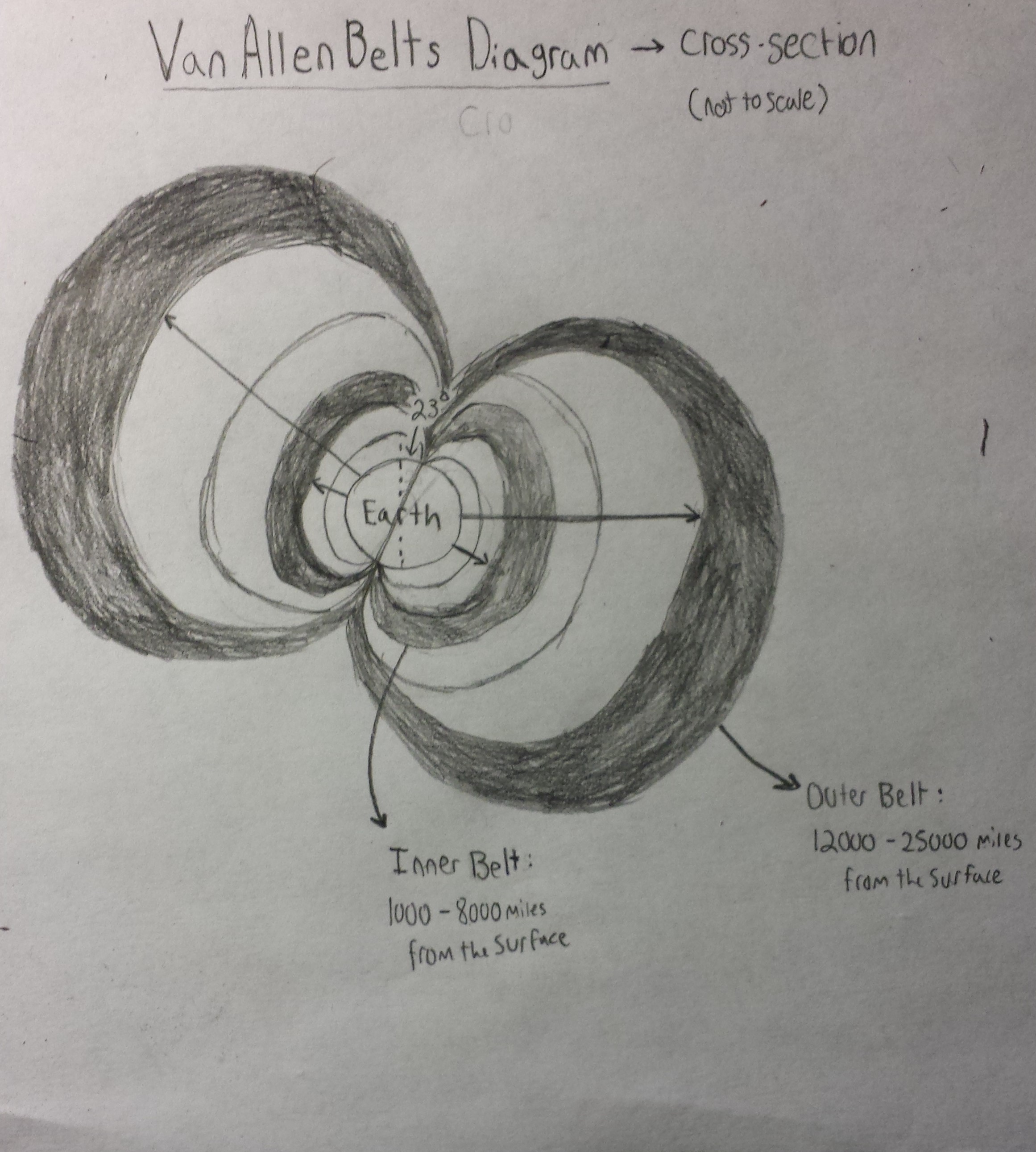
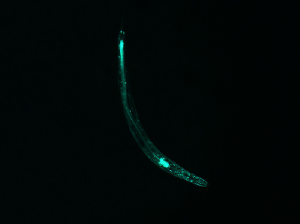
Earth’s Van Allen Belts are a naturally occurring phenomena due to the presence of the Earth’s magnetic fields. Specifically, they are two zones of space where large concentrations of high energy particles are trapped by the magnetic field lines of our planet. The zones are defined by our field lines; toroidal in shape, and encompass the planet at particular radii from the surface. Following the field lines, the regions begin from Earth’s Southern Pole and loop to its Northern Pole This is illustrated in the diagram below.

Cross-Section of the Van Allen Belts

The particles of these regions include fast moving electrons,and ions from the solar wind along with protons and other remnants of cosmic ray interactions with our atmosphere. All of these particles are electrically charged and thus their motion becomes highly constrained as they pass through our magnetic field; or magnetosphere. As they interact with our magnetic field lines, a force is exerted and influences their direction of motion. It attempts to make the particles rotate about the lines rather than allowing them to continue drifting in a straight line. Thus “sliding” begins to occur; the particles gain a spiral trajectory during which they orbit the field lines while vertically moving along them. Since the magnetic field is stronger as you get closer to Earth however the particles will stop and eventually reverse their motion as they approach the poles. This bouncing between the hemispheres establishes the permanent belts.

The constituent particles and stability of the belts however depends on the location.and thus the strength of the magnetic field. The inner belt is compact; ranging only from 1,700 km to 13,000 km above the Earth’s surface. It is made up primarily of high energy protons created during cosmic ray interactions with the atmosphere. Of the two belts, it is the most stable due to the higher magnitude of the magnetic field lines at that proximity to the Earth. While it gains high energy particles at a comparatively slow rate, it holds onto the particles for an extended period of time and reaches a much higher intensity than the other belt.

The outer belt ranges from 20,000 km to 40,000 km from the Earth’s surface and consists primarily of the ions and electrons that make up the solar wind. Due to the weaker magnetic field at that distance from Earth, the zone is tenuous and loses its particles very quickly. The constant supply of particles from the solar wind however means that the belt has plenty of material to be created from, though its dependence on solar wind particles means that its intensity fluctuates proportionally with solar wind activity. With this background information established, the information needed to created valid assumptions was gained.

2D Vector Fields:

Unfortunately, this also marks the point where my project strayed away from modeling the Van Allen Belts to a more general modeling of the Earth’s magnetic field. The initial task of modeling the magnetic field of the Earth was necessary to define the locations of the Belts with specific field lines that would be seen in the vector plot. Now with some research I found that the Earth’s field could be generally modeled as a magnetic dipole oriented with the south end pointed in the positive z direction. This model is a very basic assumption and ignores the effects of the solar wind on Earth’s magnetosphere, however the area where the Van Allen Belts are present does not get severely effected by these factors except in extreme circumstances. This means a model of a dipole will be generally accurate for our purposes. Thus the first task was to create a model of the magnetic field of the dipole.

The equation for the magnetic field of a dipole with respect to the radius was found to be

$\vec{B_{dip}}(\vec{r})=\frac{(\mu_0)(m)}{(4\pi*r^3)}(2cos(\theta)\hat{r}+sin(\theta)\hat{\theta})$

This equation was obtained from Griffiths’ Introduction to Electrodynamics. To insure the equation worked I began by applying a constant free version, evaluating only the variables. However, the equation was given in spherical coordinates which Mathematica can’t plot efficiently. To compound that issue, the command CoordinateTransform does not properly evaluate the points which led to several attempts to obtain the proper Cartesian conversion of our equation. Finally, I was able to find the command TransformedField which took into account the variables being used and allowed for a direct conversion. The code and direct conversion can be seen below.

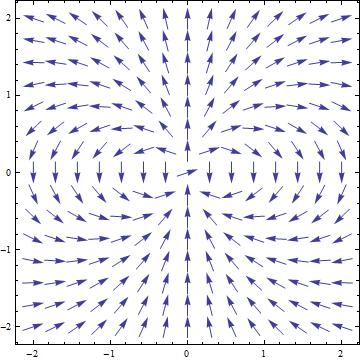
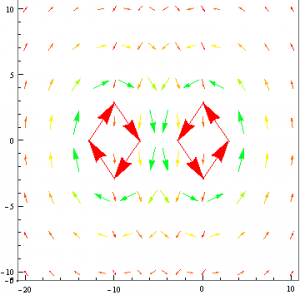
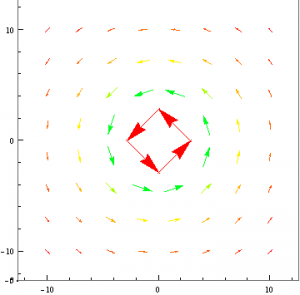
From these equations, I created a vector field of the xz plane with VectorPlot which can be seen below.

Simple vector model of the xz plane of the magnetic field of a dipole

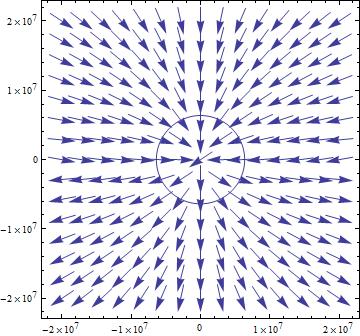
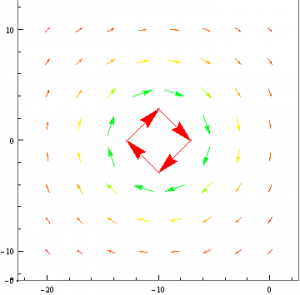
With this successful, I then applied the proper constants to the vector field components and attempted to recreated the field. These constants were the permeability of free space ( $\mu_0$ = $4\pi$*$10^{-7}$ $N$/$A^2$) and the magnetic dipole moment of the Earth ($m_{Earth}$ = $7.79$*$10^{22}$ $A*m^{2}$).The circle in the center of the graph represents the Earth, under the assumption that the Earth has a constant radius of $6.37*10^6$ m.

Model of the xz plane of the dipole’s magnetic field using Earth defined constants

Note that in this plot, the vectors seem to lack the fine structure of the previous field however the vectors are still properly oriented. They continue out from the southern hemisphere and seem to eventually loop back around and end in the northern hemisphere. I attempted a variety of scales and vector size values but no matter what, when the constants were applied to the equation they never had the same shape as the previous vector field. The other concerning aspect of the field was the fact that the vectors don’t seem to weaken as the field continues away from the Earth. It could be that the scale was just off so it was not evident, but even with the shifting of the scales, the vectors still seemed to remain the same size. The general direction and shape was obtained with these equations so I continued on to the next step.

3D Vector Fields:

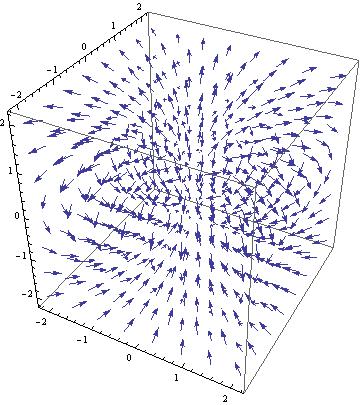
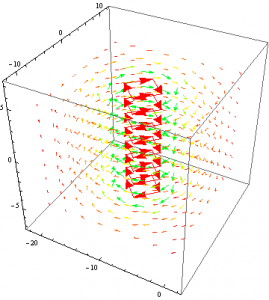
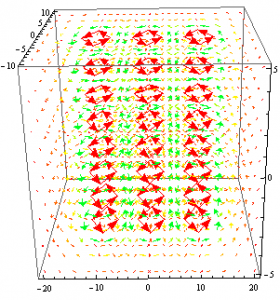
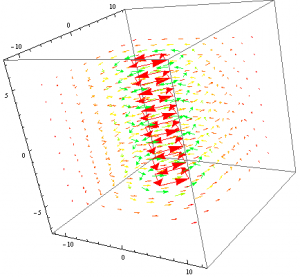
Applying the same methods as before, I used the vector field components from the obtained equation and using the command VectorPlot3D, I created a vector field of the general equation without the constants. This field can be seen below.

Simple vector model of the magnetic field of a dipole

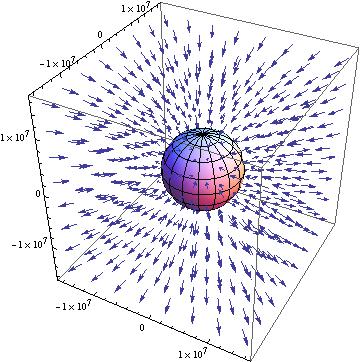
Without constants the shape of the vector field directly resembles the magnetic field of a dipole in 3 dimensions. Unfortunately, we also have the vectors not varying as expected as the distance from the origin increases. Regardless, after the success of obtaining the proper vector field shape and direction I decided to apply the proper constants to see if the shape would be altered as it was in the 2D graph. The constant applied vector field can be seen below. Once again the constants remain the same and the sphere in the center of the plot represents the Earth, assuming it is a sphere with a constant radius.

Vector model of the magnetic field of a dipole using Earth defined constants

As we can see, the same lack of detail is present when the constants are added to the vector field. However the shape and direction of the vector field are still generally correct though the fine structure is again lost. The vectors still don’t seem to vary with distance as well, which is troubling for actually plotting the field but the model does seem to accurately plot the field itself.

Further Plans:

Unfortunately it is at this point where I ran out of time and needed to call it quits on the project, with only the magnetic field of the dipole modeled. While I will discuss what I would have liked to change and go into more detail on complications within my “Conclusion”, I would like to take a moment to discuss where I wanted to continue on with this project. Specifically, next on the list would have been adjusting the vector field 23 degrees from the z-axis to account for the Earth’s natural tilt. I experimented with a few methods to do this but none of them were truly successful.

Next I would have liked to incorporate a model of the dynamo theory to account for the Earth’s magnetic field. One of the biggest assumptions made within this project was that the Earth’s magnetic field simply existed as a giant bar magnet in the surface. The magnetic field is actually generated by the motion of liquid iron present in the Earth’s outer core. Using this knowledge, I was hoping to create an animation that would allow the observer to alter the size of the planet and then the percent of the outer core took up of the interior. This would allow the observer to have a general model about how the magnetic fields change with different core sizes and thus the location of the Van Allen Belts. Knowing this, scientists could prep future scientific equipment for radiation exposure even if they needed to orbit within the Van Allen belts.

Here are my Mathematica Notebooks in case there were any questions on my code: 2D Vector Fields, 3D Vector Fields, and General Experimenting

Sources:

Griffiths, David, Introduction to Electrodynamics

Stern, David, Radiation Belts (http://www.phy6.org/Education/Iradbelt.html)

Dynamo Theory (https://courses.seas.harvard.edu/climate/eli/Courses/EPS281r/Sources/Earth-dynamo/1-Wikipedia-Dynamo-theory.pdf)

Magnets and Electromagnetism (http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/elemag.html)

Magnetic Field Conclusions

When I started this project I initially had the intention to model the magnetic fields due to a cylinder, bar magnet, and sphere. Little did I realize that while I knew that these fields should look like theoretically, modelling them would have been a great undertaking. The fields due to a bar magnet is that of a magnetic dipole and that in itself seemed as though it would have been a project. The sphere could have been modeled in two different ways: as a rotating sphere of charge, or a collection of current-carrying loops. Both were very difficult to find the magnetic field for at any given point and so I was at a loss for things to model.

I was only able to successfully plot the magnetic field due to a line of charge rather than a cylinder since I was having trouble making Mathematica plot piecewise vector functions. The plot below was all that I had to work with.

After some discussion with Professor Magnes, I decided I would take what I had, and make more complicated systems with it.

As seen in my previous Final Data post, I was able to show that if identical current-carrying wires were aligned next to each other, their resulting magnetic field would resemble that of the field due to a plane of current as the distance between them decreases.

The only problem I faced was that I could not find a way to superimpose the vector fields from my aligned wires. While this would have made my model look nicer, it is still relatively clear to understand how the field lines add together.

Next I decided I would use the same method that I used to mimic a plane of current and attempt to model a magnetic dipole. Rather than placing two identical current-carrying wires next to each other, I made one of them have a negative current. I would then plot their resulting vector fields and change the viewpoint such that only the x,y plane was seen.

Again I was faced with the issue of superimposing my two vector fields. However, I suspect that if I found a function Mathematica that would do this for me, I would have indeed modeled a magnetic dipole.

While the topic of my project was by no means a very complicated one, it would be false to say that I did not learn anything from it. My understanding of how Mathematica functions as a program has grown and I have come to appreciate its capabilities. I also learned that while something may seem simple at first in theory, it can be very complicated to achieve in reality.

Conclusion: Diffraction Patterns of C. elegans

I set out to model the diffraction patterns created by C. elegans nematodes using mathematica, specifically using the diversely useful mathematical tool of the Discrete Fourier Transform. The Transform is a quick way to find the diffraction patterns from Fraunhofer diffraction and interference (far-field diffraction). In simpler language, $\left| FT^{2} \right|$ produces the diffraction pattern, which is an analysis of the Electric field strength across the aperture, in this case, the image. The goal of this project was to produce a “library” of shapes and their corresponding diffraction patterns. However, there were many obstacles that made it necessary for me to do quite a bit of relevant research.

When I started, I did not know that the type of diffraction I was studying was Fraunhofer. Diffraction patterns are a result of the type of wave and the type of experimental setup. In this case, the light source, the aperture, and the screen were are far enough away to classify it as far-field. Mathematically, $L>>\frac{b^{2}}{\lambda}=\frac{area. of. aperture}{\lambda}$ . The fact that this is an example of Fraunhofer Diffraction makes it possible to apply the FT (on Mathematica) to yield the diffraction pattern.

I came in with some preliminary knowledge of what Fourier Transforms were in theory. In general, when applied, it changes a function’s variable dependence: $F(t) \leftrightarrow \Phi (v)$. I did quite a bit of research on the derivations of the transform and understood the matrix calculations necessary to do the transform “by hand” (see Project Plan).

To produce good-quality images, it was also necessary to do quite a bit of exploring in the Mathematica Documentation Center, becoming familiar with a variety of image manipulation commands. Those included: sharpening, brightening, finding the pixel count and dimensions, cropping, changing the color scheme to grayscale, partitioning and reassembling images manually based on the pixel dimensions, and more, depending on what degree of manipulation the image needed.

All in all, the images produced are not only pretty, but informative and now available for reference. Because it is mathematically impossible to go from the diffraction image to the shape, it is necessary to have some type of library, like the one I created, to go in that direction. (It is impossible to do it mathematically because when the Fourier Transform is applied, the phase information of the light is lost as the data is converted to the complex space.) Therefore, my “library” is useful because I have made it possible to guess the approximate shape and orientation of the worm from the diffraction pattern for some basic worm shapes. Another application for this analysis is that a compilation of several consecutive diffraction patterns shows the thrashing frequency of the worm. For example, if you took several pictures within a few seconds and found the diffraction patterns, the amount that the patterns change corresponds to the “thrashing frequency,” or the quantifiable amount that the worm wiggles.

If I were to continue this project, I would continue to build upon the library in the same manner, testing to see if different input image qualities would make a difference in the final product (if different pieces of the worms were fluorescing, if the worm was glowing a different color, etc). Finally, I would construct a real library (instead of this evolving blog site) that was easy to navigate, and generally more accessible for research.

Conclusion- RLC Circuits

Overview

In this post, I will draw conclusions from my previous final data post about both RLC circuits that I have modeled.

RLC Circuit- No Voltage Source

This RLC circuit [Figure 1] proved to be an interesting demonstration of the current in a circuit without a voltage source. The initial current running through the circuit is provided by the charged capacitor. However, this initial current undergoes damping due to the resistor in place, and the current running through the circuit pretty approaches zero pretty quickly.

[Figure 1]

My model of this circuit verifies this idea since it shows an exponential decay of the current as a function of time [Figure 2]. After about 4 seconds, there is no longer an active current running through the circuit due to the resistor. My Mathematica notebook is easily set up for changing the values of the different components, and one can easily change them to see what effect this has on the circuit.

[Figure 2]

RLC Circuit- AC Voltage Source

The second RLC Circuit that I modeled was identical to the one above, except that it had an alternating current voltage source as well [Figure 3]. This allowed it to continue to have a current present despite the effects of the resistor.

[Figure 3]

Initially, I approximated the solution to the differential equation governing the circuit by ignoring the damping terms. This resulted in a an extremely good approximation, as the damping terms should only effect the circuit’s current flow in its first few seconds. After some computational hiccups that inaccurately displayed long-term variations in the current, I went on to graphically solve the complete form of the equation and graphed it to prove that the two damping terms only had a small effect in the first few seconds of the circuits behavior[Figure 4].

[Figure 4]

Final Remarks

Given the chance to work more on this project, I would develop manipulable animations within Mathematica that would allow one to change a given variable (ex. resistance, inductance, capacitance). This would allow the reader to easily see the effects that the different components have on the circuit. This would also be helpful from an educational standpoint as an applet to someone wanting to learn more about RLC circuits, or circuitry in general.

On a final note, I managed to learn a lot more about Mathematica and its differential equation solving capabilities. Solving the equations for these circuits by hand would have been an extremely length procedure, but once I provided Mathematica with the commands in the correct syntax, it solved them much faster than any human could. This project helped me appreciate the uses of computational tools in physics, and I am very glad that they exist.

Final Data

By using the formula for the magnetic field of a wire that I derived in my preliminary data,

(1) $\begin{equation*} \mathbf{B}(s) = \left\{ \begin{array}{lr} \frac{\mu_{0}I}{2\pi s}\widehat\theta & : s > a\\ 0 & : s < a \end{array} \right. \end{equation*}$

I was able to model systems composed of current-carrying wires.

First I used the above equation and converted from Cylindrical to Cartesian coordinates. This was done because Mathematica will only plot vector fields in this form. I then plotted the resulting vector field due to a positive current.

This is exactly what we would expect to see for the magnetic field of current carrying wire as illustrated by the well known “Right-Hand-Rule”. The field lines are more intense towards the center of the of the wire while they decrease exponentially as they move further away. They are also oriented counter-clockwise since a positive current was used. Suppose now that we were to switch the current to a negative value.

As expected, the field lines behave in the same way as before expect they oriented in a clockwise fashion.

Below I changed the viewpoint of the magnetic field such that only the x,y plane is shown. This helps to visualize the field because the field does not change along the z-axis.

Now that I successfully found the Magnetic Field for a current-carrying-wire, I could make the system more complicated by adding additional wires.

Suppose that some identical wires were placed parallel to each other at some distance.

Again I changed the viewpoint such that only the x,y plane is seen.

As you can see in the above plots, the fields in between the wires have a certain type of symmetry. The field lines point in opposite directions and as they get closer to the midpoint between the to wires, they are of the same magnitude and cancel. It is safe to assume that as the distance between the wires approaches 0, the magnetic field between the wires will no longer exist.
Above and below the set of wires, the direction of the field lines due to each wire is the same: +x below the wire and -x above the wire. Coincidentally, this shares similar traits to the magnetic field due to a plane of current; the field lines above and below the plane will point either in the positive or negative x direction while there is no magnetic field anywhere along the plane itself. This shows that a plane of current can be viewed as a collection of parallel wires with no distance between them.

Suppose now that I had two wires parallel to each other but rather than having both wires having the same current, they are opposite to each other.

If Mathematica were able to superimpose the magnetic fields from the different wires, I suspect that the resulting field would resemble that of a magnetic dipole. However, I have not been able to find a function that will do this given two different vector fields and am limited by time to model a magnetic dipole using an alternative method. Nevertheless, the field that I was able to model does share some similarities to that of a dipole. The symmetry of the field lines are the same as those of a dipole. This is a result of two equal and opposite currents.

Mathematica Notebook

References:

Griffiths’ Introduction to Electrodynamics 4th edition

Final Data- RLC Circuits

Overview

After talking with Professor Magnes after my preliminary results, I decided to first look at an RLC circuit with no voltage source, which is much simpler to model. Doing this allowed me to better understand the mechanism behind the circuitry and gain more experience with Mathematica as well.

After doing so, I returned to my progress with an RLC circuit with a voltage source and determined that the odd structural variations with the long-term structure were due to computational limitations of Mathematica (again, thanks to Professor Magnes for the suggestion). Since I had only developed the approximate solution, I went on to graphically solve for the full solution and see what the damping terms did to the solution.

Note: I included the findings from my preliminary data in this final data post (so it may seem redundant for a portion in the middle) since it was used in my final results as well. I figured it helps to have everything in one place for the reader.

RLC Circuit with no voltage source

Circuit Diagram and Mathematics

The first circuit we will examine is an RLC circuit with no voltage source. The initial potential difference is stored on the capacitor, but can not be recharged due to the lack of a voltage source. The three main components of this circuit are a resistor (R), an inductor (L), and a capacitor (C).

[Figure 1]

The differential equation that governs this circuit is

$LI''(t)+RI'(t)+\frac{1}{C}I(t)= 0$ [1]

where L is the inductance, R is the resistance, C is the capacitance, I is the current through the circuit (which is the same at all places at one time since this is a series circuit), and t is the time.

Solving the Differential Equation

We can set arbitrary values for R, L, and C since they depend on the specific pieces of equipment themselves:

Inductance= 1 Henry
Resistance= 10 ohms
Capacitance= .1 farads

In Mathematica, the command to solve [1] looks like

$\text{DSolve}\left[\frac{\text{Current}(t)}{\text{Capacitance}}+\text{Inductance} \text{Current}''(t)+\text{Resistance} \text{Current}'(t)=0,\text{Current}(t),t\right]$ [2]

which when solved, yields:

$I(t)= c_1 e^{-8.87298 t}+c_2 e^{-1.12702 t}$ [3]

Completing the Full Solution via Graphical Solving

The two constants depend on the initial conditions of the circuit, which must satisfy Ohm’s Law of $I=\frac{V}{R}$ . So, the initial current in the circuit must be 0.1 amps. Using a graphical guess-and-check method in Mathematica, I determined the value of the two constants to be approximately 0.05 each, resulting in a solution that is given by

$I(t)= 0.05 e^{-8.87298 t}+0.05 e^{-1.12702 t}$ [4]

The plot of this equation gives us the current as a function of time, and looks like

[Figure 2]

This graph tells us that although the RLC circuit starts out with a current of 0.1 amps, it quickly dies down due to the lack of a voltage source and is not very interesting after a few seconds. Refer to the upcoming conclusion blog post for a bit more analysis.

Now, lets examine the RLC circuit with a voltage source (much more interesting!)

RLC Circuit with AC voltage source

Circuit Diagram and Mathematics

Now we can model an RLC circuit that consists of a capacitor, voltage source, resistor, and an inductor. To easily visualize this, I have constructed a basic circuit diagram (Figure 3).

(Figure 3)

The differential equation that governs this RLC circuit is given by

$LI''(t)+RI'(t)+\frac{1}{C}I(t)= E_{0} \omega cos(\omega t)$ [5]

where L is the inductance, R is the resistance, C is the capacitance, I is the current, $\omega$ is the resonant angular frequency, $E_{0}$ is an initial value dependent on the voltage source, and t is the time. The inductance (L), resistance (R), and capacitance (C)are all determined by their respective circuit components, which are easily changed out for different ones. $\omega$ depends on the inductance and capacitance, and its value is given by

$\omega =\frac{1}{\sqrt{LC}}$ [6]

What we have left in terms of variables are current (I) and time (t). For our purposes, time is the independent variable, which leaves the current in the circuit at any time to be the dependent variable. Now that we have established this, we can solve our differential equation [5] for current as a function of time ( $I(t)$ ).

Solving the Differential Equation

In order to solve [5], I will use the equation solving powers of Mathematica. In particular, the DSolve function is used. When plugged into Mathematica, the input line looks like:

$\text{DSolve}\left[\frac{\text{Current}(t)}{\text{Capacitance}}+\text{Inductance} \text{Current}''(t)+\text{Resistance} \text{Current}'(t)=E_{0} \omega \cos (\omega t),\text{Current}(t),t\right]$ [7]

We must set values for resistance, inductance, capacitance, and $E_{0}$ . For this solution, I chose the same values as the first circuit :

Inductance= 1 Henry
Resistance= 10 ohms
Capacitance= .1 farads
$E_{0}$ = 1 Volt

When the command is run with the above values set, Mathematica generates the general solution, which is:

$I(t)=c_1 e^{-8.87298 t}+c_2 e^{-1.12702 t}+0.040824(-Cos(3.162t)+e^{6.661*10^-16t}Cos(3.162t)-0.3564Sin(3.162t)+2.806e^{6.661*10^-16t}Sin(3.162t))$ [8]

First, lets make sure that this solution is reasonable. The known form of the solution to the equation for such a circuit is given by:

$I(t)=c_1 e^{r_{1}t}+c_2 e^{r_{2}t}+Asin(\omega t-\varphi )$ [9]

The form of our equation [8] seems to match up pretty nicely with this known solution [9]. Now, lets examine [8] in more detail.

Our solution [8] looks a little daunting, but we can break it down into its components. The first two terms have constants that depend on the initial current running through the system, i.e. when $I(t)=I(0)$ . However, we can approximate the equation by only looking at the last term, which is a superposition of sin and cosine functions along with a couple exponential terms thrown in. The reason that we can apply this approximation is that the first two terms “damp out” quickly, and thus have exponentially less of an effect as time progresses. The reader may still be curious to see how much of an effect these terms have on the current flowing through the system: to that I say don’t worry! After my initial approximation, I will solve for these constants and compare the two cases.

Approximate Solution and Graphs

For now, we will deal with the approximate solution, which is:

$I(t)=0.040824(-Cos(3.162t)+e^{6.661*10^-16t}Cos(3.162t)-0.3564Sin(3.162t)+2.806e^{6.661*10^-16t}Sin(3.162t))$ [10]

Now that we have this equation, we can use Mathematica to give us an idea of what the changing current looks like over a longer period of time. Figure 2 shows the current in the circuit as a function of time ( $I(t)$ ) plotted over a 30-second interval.

(Figure 4)

This looks like something we would expect! A sinusoidal wave that describes the changing current over time, just like our equations dictate. But, this is a short time-scale. What happens when we look at the changing current over a longer period of time? In Figure 3, I show the changing current over a longer time period (3000 seconds/50 minutes). In Figure 4, I repeat the process, but with the timescale being 5 years.

(Figure 5)

(Figure 6)

In both Figures 5 and 6, we see some very interesting long-term variations in the current. Why does this occur?

Computational Limits

It is clear that Mathematica is displaying some odd variations that do not seem to have a set pattern. To investigate this and determine its cause, lets look closer at a range of time where the current seems to be irregular in the previous two figures. Specifically, lets look at the time scale between 300 and 400 seconds because it seems to have very strange behavior.

[Figure 7]

Looking at the graph above, we see that it looks completely normal! There are no strange variations and the current continues the predicted sinusoidal trend. This leads me to the conclusion that Mathematica has limitations that caused the irregular variations that we saw before, and that they do not actually exist in the data/circuit.

Completing the Full Solution via Graphical Solving

The next and final step in completing our model is accounting for the two initial terms that we left out. Lets take another look at the full equation.

$I(t)=c_1 e^{-8.87298 t}+c_2 e^{-1.12702 t}+0.040824(-Cos(3.162t)+e^{6.661*10^-16t}Cos(3.162t)-0.3564Sin(3.162t)+2.806e^{6.661*10^-16t}Sin(3.162t))$ [11]

We can see that they are exponential functions with a separate constant for each term. Solving for these constants quantitatively can prove to be difficult, so I will attempt to solve for them via a guess-and-check method using plots in Mathematica. I need to match the initial condition so that Ohm’s law is satisfied. So, $I=\frac{V}{R}$ must hold in the initial state. This means that the initial current must be 0.1 amps. Lets try a few values for $C[1]$ and $C[2]$ and figure out graphically what they should be.

First, lets try values of 0.5 for each, resulting in the following equation:

$I(t)=0.5e^{-8.87298 t}+0.5e^{-1.12702 t}+0.040824(-Cos(3.162t)+e^{6.661*10^-16t}Cos(3.162t)-0.3564Sin(3.162t)+2.806e^{6.661*10^-16t}Sin(3.162t))$ [12]

The graph resulting from this equation is:

[Figure 8]

We can see that the initial current that this combination of constants is too high! It gives 1.0 amps, when we are looking for 0.1 amps.

Lets try slightly higher values for each, as well as having different values for the two. The equation that results is:

$I(t)=2e^{-8.87298 t}+3e^{-1.12702 t}+0.040824(-Cos(3.162t)+e^{6.661*10^-16t}Cos(3.162t)-0.3564Sin(3.162t)+2.806e^{6.661*10^-16t}Sin(3.162t))$ [13]

Which produces the following graph:

[Figure 9]

Looks like we have gone the wrong way with our guess! Lets try lowering both the constants to arrive at the correct graphical solution (in reality, this took me many more iterations of guessing and checking):

$I(t)=0.05e^{-8.87298 t}+0.05e^{-1.12702 t}+0.040824(-Cos(3.162t)+e^{6.661*10^-16t}Cos(3.162t)-0.3564Sin(3.162t)+2.806e^{6.661*10^-16t}Sin(3.162t))$ [14]

Which results in the following graph:

[Figure 10]

The Graphical Solution

Now that we have arrived at the correct graphical solution, lets change the scaling of the graph to better match that of [Figure 2], which was the initial approximation that did not take into account the two damping exponential terms.

[Figure 11]

My conclusion from this final data will follow in my next blog post.

Resources

1. Circuit Diagram Maker- http://www.circuit-diagram.org/

2. The RLC Circuit- University of British Columbia- http://www.math.ubc.ca/~feldman/m121/RLC.pdf

3. Mathematica Cookbook by Sal Mangano

4. Electronic Circuit Analysis for Scientists by James A. McCray and Thomas A. Cahill

5. Dynamical Systems with Applications using Mathematica by Stephen Lynch

6. Class Notes- Mathematics 228 (Methods of Applied Mathematics) taught by Matthew Miller

Mathematica Notebook

https://drive.google.com/file/d/0B3mtB6CQNnpjbXROcHl0VURzYlE/edit?usp=sharing

Final Data and Conclusion: Scattering in the Interstellar Medium (ISM)

The goal of my project was to explore a relatively well understood model for light scattered off spherical particles in the interstellar medium (ISM): Mie theory. Over the course of my investigations I switched my inquiry from attempting to derive and plot the asymmetry parameter, g, to plotting the extinction efficiency $Q_{ext}$. Note: I have included portions from my preliminary data post in order to maintain clarity and continuity. Portions from the preliminary post are still relevant and will remain likewise.

Final Reflections

An important question emerges in the study of scattered light in the interstellar medium (ISM). Why use the Mie solutions to Maxwell’s equations as opposed to the Rayleigh or Debye methods for modeling this scattering? As with many other methodological decisions, the answer lies in the physical parameters and observational requirements of the system that I’m trying to model. Optical observational data of extinction due to dust grains as a function of wavelength is denoted by: $A_\lambda$ and this observed data necessitates that the extinction be inversely proportional to wavelength:

$A_\lambda\propto\lambda{^-1}$

i.e. the wavelength must be approximately the size of the grains in question. Only with that dependency will the the model fit the data. Wavelength dependencies for Rayleigh and Debye scattering do not provide the necessary proportion.

Asymmetry parameter, g

As indicated in my preliminary data, modeling the Mie solutions to Maxwell’s equations for scattered light by spherical particles has proven tricky. Ultimately my attempt to plot the asymmetry parameter, g, was unsuccessful, but I was able to plot another grain property instead, the extinction coefficient $Q_{ext}$, versus dimensionless size parameter x (which I will explain in a later subsection of this post). My Mathematica code for the asymmetry work is attached at the bottom of this post as it was in the preliminary data post, but I updated the notebook since I commented on those results and have concluded that work with a derivation of the scattering coefficients $a_n$ and $b_n$.

Below I detail my journey through the asymmetry parameter, g, within of through Mathematica 9 and the processes that comprised those investigations. I find that detailing where I made it up through is important in the process of fixing my work in the future, in addition to being a pedagogically useful process (learning through mistakes!).

I made some simplifying (and yet physically relevant) assumptions. The spherical grains will be water ice with an index of refraction of n=1.33. The vacuum will have an index of refraction of n=1. Items [k, 1] and [k, 2] are coefficients for the imaginary portion of the indices of refraction. I have assumed a wavelength within the optical spectrum. [K, 1] – [K, 3] are the wave numbers for the different indices and included are the wavelengths necessary to derive those wave numbers. Lastly I have provided an arbitrary, placeholder grain radius.

I have also defined grain size parameters, necessary for the calculation of the coefficients $a_n$ and $b_n$, shown below.

Helpfully, Mathematica has Bessel functions built in. I used them in my exploration into modeling the asymmetry parameter. Dependent on interstellar grains properties, i.e. if it’s dielectric and thus has a real index of refraction or it has a complex index of refraction (impure water ice grain), the Bessel or Ricati-Bessel function will change.

Lastly, here’s my code for the coefficients, $a_n$ and $b_n$. $\alpha$ and $\beta$ have been replaced with q, but those values are still the size parameters.

$Q_{ext}$ v. Size Parameter

In exploring scattering within the interstellar medium (ISM), it is possible to define an extinction efficiency $Q_{ext}$. This efficiency is dependent on index of refraction, m, and can be approximated by

$Q_{ext}\approxeq(8/3)x^4|{\frac{m^2-1}{m^2+2}}|^2$

where $x=2\pia/\lambda$ and is the dimensionless size parameter, depending on grain radius, a.

In Mathematica I began by defining a wavelength (red light in microns) and the indices of refraction. Note that indices $m_2$ and $m_3$ (denoted by d2, d3) involve complex components. These components are necessary because of the nature of the grains, which in this case I assumed to be made of different ices.

Next I defined the size parameter, $x=2\pia/\lambda$ as well as interior terms for the $Q_{ext}\approxeq(8/3)x^4|{\frac{m^2-1}{m^2+2}}|^2$ equation; specifically, I define ${\frac{m^2-1}{m^2+2}}^2$.

Next I combined the previous bits of Mathematica code to get the actual values for $Q_{ext}$

and then applied a transpose on my data points (where x-values need to be the size parameter, x, and y-values need to be $Q_{ext}$) to be able to ListPlot the three $Q_{ext}$ v. size parameter plots. Transposes shown below!

Now I could create my plots! Note that the scales are arbitrary, what I am interested in is the behavior of the plots. This behavior dictates differences in ice grain extinction efficiencies dependent on size and index of refraction. Below are my three plots:

Qext v size parameter x (m = 1.33)

Qext v size parameter x (m = 1.33-0.09i)

Qext v size parameter x (m = 1.27-1.37i)

Conclusion

While the plots for Qext v size parameter x for m=1.33 and m=1.33-0.09i show a positive exponential trend, the final plot shows quite the opposite behavior. For grains with indices of refraction that have complex components, extinction efficiency versus size parameter plots should indicate a damping in the plot. So I do have some confusion with my plots. The third plot clearly indicates a variation in behavior when compared to the first two, but the second plot (of an extinction efficiency involving a complex index of refraction) should behave similarly to plot 3, not plot 1. This is a good transitioning point into where this work could go in the future – examining whether or not the extinction efficiency versus size parameter plots were indeed done correctly. Mathematica is lenient neither in syntax nor its learning curve! In the future it would also be useful to try and continue my work on the asymmetry parameter, but that might take a greater commitment than just fixing what may be incorrect with the extinction efficiency plots.

I have learned a great deal over the past few weeks about research and computational modeling. I have truly grown in respect to my appreciation for modeling and all the hiccups and hurdles that come with learning how to effectively and efficiently use Mathematica. While my explorations into the asymmetry parameter, g, were unsuccessful at producing a plot, I am very proud at being able to produce plots of extinction efficiency $Q_{ext}$ versus size parameter, x. The results, while not ideal, still reflect trends in the physical behavior of the system – in this case the light scattered by spherical particles in the interstellar medium (ISM).

Resources

Introduction to Electrodynamics, 4th ed. by David J. Griffiths
Physics of the Galaxy and Interstellar Matter by H. Scheffler and H. Elsässer
Interstellar Grains by N.C. Wickramasinghe
Physical Processes in the Interstellar Medium by Lyman Spitzer, Jr.
The scattering of light, and other electromagnetic radiation by Milton Kerker
Mathematica 9 Help Documentation Center (the most valuable resource!)

Mathematica notebooks:

https://drive.google.com/file/d/0B_r-c0PTUHZldHVNREtrWHlzZXc/edit?usp=sharing

https://drive.google.com/file/d/0B_r-c0PTUHZlNVh5emxudUJrRDA/edit?usp=sharing

Final Data: Diffraction Patterns of C. elegans (revised)

Listed below are five sets of data (3-7), two images each. On the left is the photograph of the fluorescing worm. To the right is its corresponding diffraction pattern, produced with Mathematica.

First, a few comments:

Notice that each worm shape contains a different symmetry (or lack of symmetry). However, every diffraction pattern is symmetrical. The two images tend to share some symmetrical qualities, as noted below each image.

These diffraction patterns are due to the fluorescing parts of the worm (GFP, or green fluorescing protein). I believe that because of my image manipulation (converting to grayscale and brightening the image significantly), the diffraction pattern is approximately due to the entire worm and not just the fluorescing parts.

On that note, I’d like to discuss the parameters I used for image manipulation and Fourier Transforming.

The Fourier Parameters I chose were {0, 1} . These are the default parameters when using the FT command on Mathematica. I chose them among the three most common by ruling out the other two: {-1, 1} is used for data analysis (which I was not doing), and {1, -1} is used for signal processing (also irrelevant to my project). My choice of parameters specified the conventions I wanted the program to use when applying the transform.
The command ImageAdjust [image, {a, b}] adjusts the contrast of the image by a and the brightness by b. For most of my images, I adjusted the contrast by the same amount, but changed the brightness differently for each photo depending on my judgement.
I divided the images by hand and reassembled them according to the image dimensions, rectangles of dimension {col/2, row/2} (where col = the number of pixels in each column of the image, and row = the same for each row). I could have use the command RotateRight, but I did not figure that out until after I developed this equally effective algorithm.

IMAGE 3

This image has axial symmetry perpendicular to the axial symmetry of the worm. The worm is mostly linear, and so is the diffraction.

(complete file for image 3: book 3 )

IMAGE 4

See comment for image 3.

(complete file for image 4: book 4 )

IMAGE 5

Although this does not have an “inversion center” (the worm does not complete a loop), it is significantly less straight than the first few examples. Correspondingly, the diffraction pattern has an axial symmetry perpendicular to the “axis” of the worm. However, it splays out to a higher degree, indicating that the area of the pattern corresponds with the curvature of the worm.

(full file for image 5: book 5 )

IMAGE 6

This further backs up my hypothesis from image 5. The curvature of the worm is great and the area of the pattern is also large. However, this worm does have a sort of “inversion center.” The diffraction image has an eye in the center, which is different than all of the preceding images. The curvature of the worm greatly effects the produced image, which is not surprising, but the overall shape of the image changes dramatically. With more circular worms, an “eye” is formed in the center of the diffraction pattern, and the pattern here has both some rotational symmetry and axial symmetry. With straighter worms, the diffraction is much more linear, containing only axial symmetry.

(full file for image 6: book 6 )

IMAGE 7

See comment for image 6.

(full file for image 7: book 7 )

Preliminary Data: Magnetic Field Modeling

In this post I will describing the specific charge distributions that I will be modeling and showing a brief derivation for the formulas I calculated.

Cylinder:

Problem 5.14 of Griffiths’ Introduction to Electrodynamics 4th edition describes a long cylindrical wire of radius a and steady uniform flowing current I over the outside surface of the cylinder. The magnetic field outside of the wire can be easily found by using Ampere’s Law.

$\oint \mathbf{B}\cdot dl=\mathbf{B}\oint dl=\mathbf{B}2\pi s=\mu_{0}I_{enc}=\mu_{0}I$

(1) $\begin{equation*} \mathbf{B}(s)=\frac{\mu_{0}I}{2\pi s}\widehat\theta& : s > a \end{equation*}$

When looking at points inside of the cylinder, or $s<a$ , $I_{enc}=0$ and so we know that:

(2) $\begin{equation*} \mathbf{B}(s)=0& : s < a \end{equation*}$

Combining our two cases in (1) and (2) we have:

(3) $\begin{equation*} \mathbf{B}(s) = \left\{ \begin{array}{lr} \frac{\mu_{0}I}{2\pi s}\widehat\theta & : s > a\\ 0 & : s < a \end{array} \right. \end{equation*}$

This is plotted below using Mathematica.

Cylinder

As expected, the magnetic field follows the commonly known right-hand-rule where the direction of the current curls around the direction of current.

Plane -> Slab :

Problem 5.15 of Griffiths’ Introduction to Electrodynamics 4th edition, a thick infinite slab extending from z=-a to z=a carries a uniform volume current $\mathbf{J}=J\widehat x$ . The magnetic field inside of the slab can found using Ampere’s Law again.

$\oint \mathbf{B}\cdot dl=\mathbf{B}\oint dl=\mathbf{B}l=\mu_{0}I_{enc}=\mu_{0}IzJ$

(4) $\begin{equation*} \mathbf{B} = -\mu_{0}Jz\widehat y & : -a > z > a \end{equation*}$

When looking at point outside of the slab, our $I_{enc}=\mu_{0}IaJ$ , and so,

(5) $\begin{equation*} \mathbf{B} = \left\{ \begin{array}{lr} -\mu_{0}Ja\widehat y & : z > a\\ \mu_{0}Ja\widehat y & : z > -a \end{array} \right. \end{equation*}$

Sphere -> Ring:

After some research and individual work, I have come to realize that the magnetic field of either rotating conducting sphere or a spherical solenoid is very complicated. I decided to simplify the distribution to two dimensions rather than three for now. A sphere can be viewed as a collection of disks or rings, so I derived the formula for the magnetic field of a ring with radius R and steady current I .

By setting our coordinate system at the center of the ring, we know that the horizontal components of the magnetic field will cancel out through symmetry and the principle of superposition, and we are left with only the vertical component. This leaves us with:

$\mathbf{B(z)} = \frac{\mu_{0}I}{4\pi}\int \frac{dl}{\mathbf{r}^2}cos\theta$

where $\theta$ is defined as the angle between the wire and our position vector $\mathbf{r}$ . It follows then that

(6) $\begin{equation*} \mathbf{B(z)}=\frac{\mu_{0}I}{2}\frac{R^2}{(R^2+z^2)^{3/2}} \end{equation*}$

References:

Griffiths’ Introduction to Electrodynamics 4th edition

Mathematica Notebook:
https://drive.google.com/file/d/0B4ANWxS26h4FRE53d0d5aFRaN0U/edit?usp=sharing

Preliminary Results: Mie Scattering and the Interstellar Medium (ISM)

Reflections

$A_\lambda\propto\lambda{^-1}$

Asymmetry parameter, g

Modeling the Mie solutions to Maxwell’s equations for scattered light by spherical particles has proven tricky. My attempts so far at getting my Mathematica code to work have hit a bit of a snag, with a plot of the asymmetry parameter, g, versus grain size getting stuck on execution of the code (“running”). I am looking into the possibility that I am unable to execute code due to my laptop’s computational strength – a factor that I entirely did not rule into my planning when I laid out my timeline for the project.

Below I’ve laid out my own navigations through Mathematica 9 and the ongoing process of modeling. I made some simplifying (and yet physically relevant) assumptions. The spherical grains will be water ice with an index of refraction of n=1.33. The vacuum will have an index of refraction of n=1. Items [k, 1] and [k, 2] are coefficients for the imaginary portion of the indices of refraction. I have assumed a wavelength within the optical spectrum. [K, 1] – [K, 3] are the wave numbers for the different indices and included are the wavelengths necessary to derive those wave numbers. Lastly I have provided an arbitrary, placeholder grain radius.

I have also defined grain size parameters, necessary for the calculation of the coefficients $a_n$ and $b_n$, shown below.

Part of the complexity and my uncertainty in my code comes in trying to define a complex conjugate function used in the derivation of the Ricati-Bessel and Bessel functions. Below I’ve included the complex conjugate function that I’ve been utilizing.

Helpfully, Mathematica has Bessel functions built in, what I’ve attempted with them is listed below. Note that I am using density as a means of utilizing the Ricati-Bessel functions (wave functions) on a spherical grain. Depending on an interstellar grains properties, i.e. if it’s dielectric and thus has a real index of refraction or it has a complex index of refraction (impure water ice grain), the Bessel or Ricati-Bessel function will change.

Lastly, here’s my code for the coefficients, $a_n$ and $b_n$. $\alpha$ and $\beta$ have been replaced with q, but those values are still the size parameters.

On a side note, this snag has altered my perspective on the nature of computational modeling. I better appreciate the power and growing accessibility to supercomputing.

Resources

Introduction to Electrodynamics, 4th ed. by David J. Griffiths
Physics of the Galaxy and Interstellar Matter by H. Scheffler and H. Elsässer
Interstellar Grains by N.C. Wickramasinghe
Physical Processes in the Interstellar Medium by Lyman Spitzer, Jr.
The scattering of light, and other electromagnetic radiation by Milton Kerker
Mathematica 9 Help Documentation Center (the most valuable resource!)

Mathematica notebook: https://drive.google.com/file/d/0B_r-c0PTUHZldHVNREtrWHlzZXc/edit?usp=sharing

Modeling and Experimental Tools with Prof. Magnes

Ideal for getting ideas and feedback on upper level physics tools.

Category Archives: Mathematica

Van Allen Belt Modeling – Final Data

Magnetic Field Conclusions

Conclusion: Diffraction Patterns of C. elegans

Conclusion- RLC Circuits

Final Data

Final Data- RLC Circuits

Final Data and Conclusion: Scattering in the Interstellar Medium (ISM)

Final Data: Diffraction Patterns of C. elegans (revised)

Preliminary Data: Magnetic Field Modeling

Preliminary Results: Mie Scattering and the Interstellar Medium (ISM)