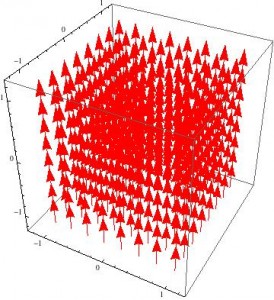
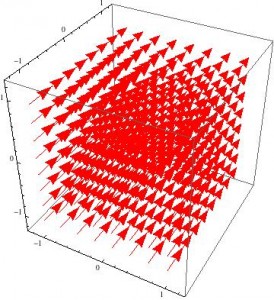
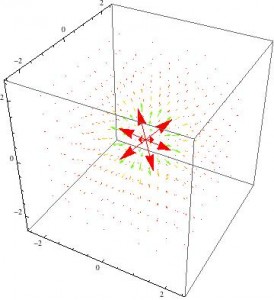
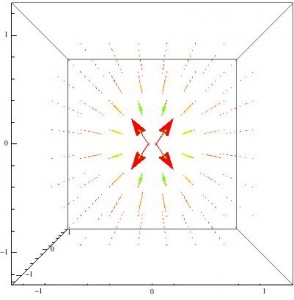
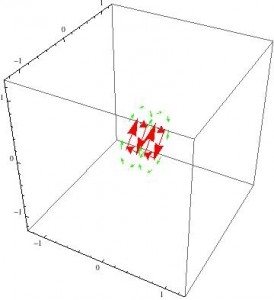
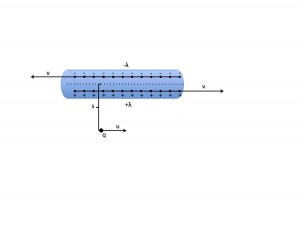
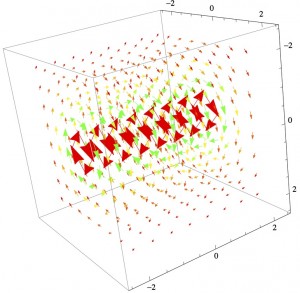
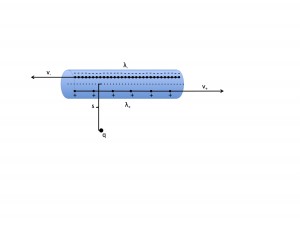
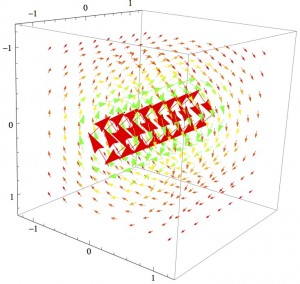
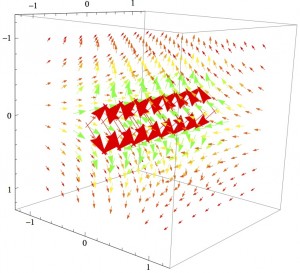
While I did succeed in creating a model that allowed the user to view the field at different speeds, it only managed to show the direction and relative magnitude compared to the rest of the current fields. If I were to continue with this project, I would attempt to improve it in several ways.
-First, I would try to find a way to make Mathematica account for the absolute magnitude of the fields so that the uniform fields would appear to change as the speed was varied. This might be accomplished by using equipotential surfaces rather than vector fields.
-Second, I would write code such that the user could simply input (or maybe copy and paste) a particular E-field equation for a rest frame, and the program would interpret the equation and produce the vector plots with sliders as shown in my model.
-Third, I would model more discrete situations rather than infinite distributions of charge or current so that the changes in field would be more visible.
-Fourth, I might consider a different type of plot, since Mathematica seems to deal with this kind of plot poorly. For instance, a static plot of E versus v and B versus v at a single point in space might better show the changing relative magnitudes of the fields.
That being said, this project was successful in several regards. It emphasizes the interplay of electric and magnetic behaviors when considered in moving reference frames, and at least in the case of the point charge, it allows for an examination of the changing shape of the fields at different speeds. It also sets up the framework for being able to model more complex systems by providing a proof-of-concept using simpler cases. Therefore, this project successfully modeled the fundamentals of relativistic electromagnetism, and provides a good foundation for a more in-depth exploration.