Describe your project

For our project, we investigated the wi-fi signal on campus. We thought it would be a good idea to find locations on campus that had good internet connection and speed. We began by selecting some of the more popular study spaces on campus such as the main library, the Retreat, the Deece, the Old Bookstore, and the Bridge Building. Our goal was to scientifically discern whether or not there exists a location on campus with the “best” wi-fi signal strength and speed. For this, we utilized two different types of equipment, a Radio Frequency meter and two smartphones. The RF meter was used to record data regarding the strength of the signal in a given location, while the smartphone app was used to measure the data rate transfer or the signal speed. We hoped if our data proves there to be a superior wi-fi signal, to convey this information to our peers in order to enhance their studying and learning experience while at Vassar.

Present your results.

What do your results mean?

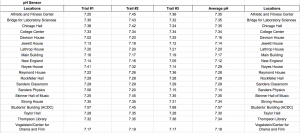
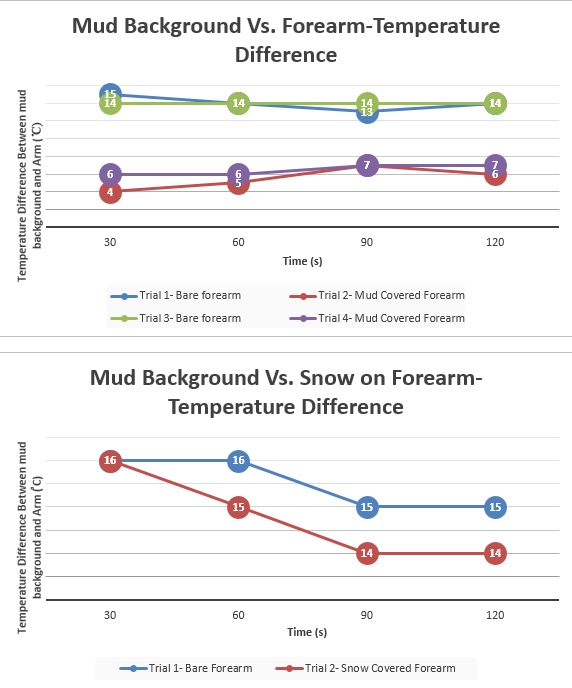
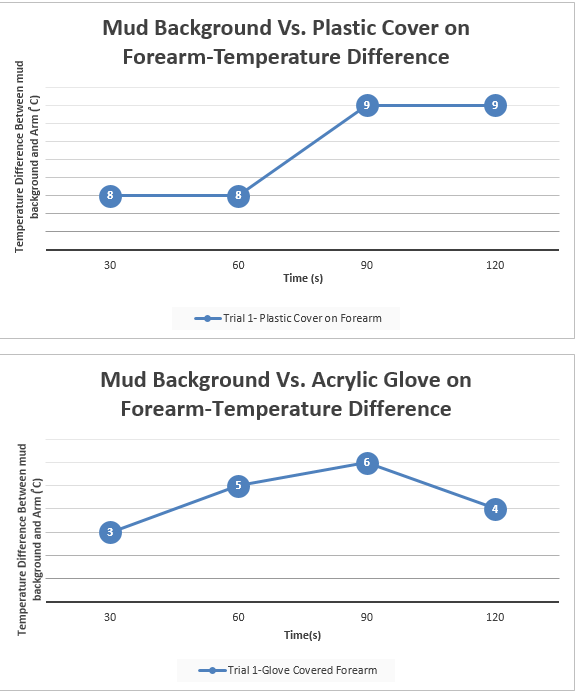
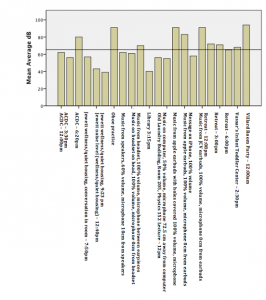
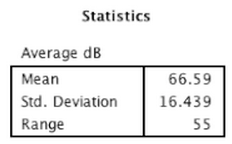
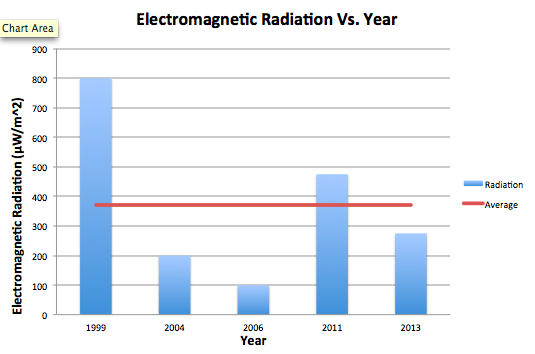
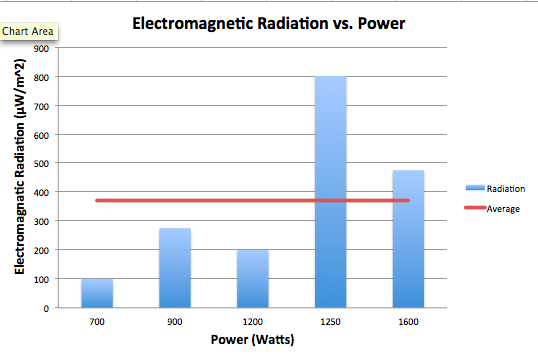
For our data, we collected two different types of data. Our first set of data consisted of collecting data based on the rate of data transfer from two different school network, Student Secure and eduroam. Using a smartphone app, data was collected in Mbps, or megabits per second, which measures the rate at which data was received by our smartphones. The locations with the highest Mbps had the fastest rates of data transfer meaning that content has the ability to load information faster than at other locations. Our data show that when connected to Student Secure three locations consistently had the highest rates of data transfer: Main Library, Library Basement, and the Deece. The data collected at these three locations when connected to Student Secure all had Mbps around 150, except for the data collected in the Library Basement over 120 seconds which had a Mbps of 107.6. Another trend that we noticed was that when connected to Student Secure, the Bridge Building had the slowest Mbps rate over all three time frames. This was especially intriguing considering that it is an academic building and one would expect it to have a fast, reliable connection but the data contradicts this. Maybe this is because the new building is new and it hasn’t gotten many updates on the wi-fi server. When analyzing the data taken when connected to the eduroam network, there were not any immediately noticeable trends. The data appears to be scattered and doesn’t seem to be any location with exceptionally fast wi-fi. The data fluctuates by location and through time frames.  Not only were these the highest rate when averaged over three different time periods, but they were also considerably higher than the rest of the location. The results represent the average amount of data that was transferred over two of the popular wifi networks on campus and the strength of the radio frequency level that was emitted over two minutes. For the data collected on the RF meter, a trend persisted where the Deece wi-fi signal strength was considerably low compared to the other locations.This perhaps has something to do with a number of people that are usually at the Deece and using the networks or with the overall spacious design of the building. Other than that, all three axes had consistent signal strengths but they were very low when compared to the Library Basement signal. For all the data collected at the z-axis, the library basement had the strongest signal strength. This is interesting because the library basement had the third highest values in terms of rate. Perhaps this shows an inverse relationship between rate and signal strength. This relationship could also be explored with the data from the Old Bookstore and Retreat. The Old Bookstore and Retreat consistently had some of the lowest rates, however, once we measured the strength they surpassed the Bridge Building and Deece, which was the inverse of what we saw in terms of rate. There are many ways to interpret this data, however, none of them make conceptual sense. It would be incorrect to assume that the stronger the wifi, the slower the rate. However, this question would be better answered with more data and less variability. As seen in the graphs, there were interesting trends in fluctuations. The strengths on each axis would range from very large values to very small values as seen with the Deece. No trends can truly be drawn from the strength because it is so variable.     

Were your results as predicted?

When we first started the project we expected the library basement to have the highest signal strength and data transfer, then the main library, the bridge, the library basement, the old bookstore, the retreat, and then the deece. Due to the library being the commonplace to study and do work and being built for that purpose specifically, we expected the library to have the strongest signal.Unfortunately, the data did not turn out how we predicted. For the RF meter, the data was very inconsistent throughout the various locations for the x,y, and z-axis. signal strength.Overall the library basement for the x,y, z and average all showed that the library basement had the highest signal strength. But the wifi app data greatly differed greatly from what we expected and from each other over time. For student secure, the main library and the library basement was in the top three for all three of the time frames, while for eduroam the library basement and the bridge were fairly consistently in the top two. Overall, the library basement which we expected to to be the third highest in signal strength and rate of data transfer was the relatively the highest.

What science did you learn during this project?

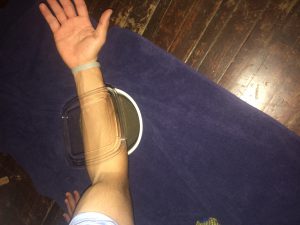
During this project, we used the RF meter and an app on our phone called Wi-Fi Sweetspots. The RF meter allowed us to calculate radio frequency levels that were being emitted. Radio frequency is associated with the electromagnetic spectrum and the spreading of radio waves. When the RF current is sent out it releases an electromagnetic field which goes through space allowing wireless technology to work. The units of the RF meter was amperes per meter which is a unit of magnetic field strength. The wi-fi app records the average rate of data that is being transferred on different wifi networks. This was measured in megabits per second which is one million bits per second with bits being a unit of data. The higher the megabits per second, the faster the connectivity.

How does our project fit in with current science/technology?

The world today is a digital one where nearly everything is run by technology. The world is constantly changing and with it, technology is advancing. Because technology is so fast-paced, it is important to have a reliable connection and wifi allows for this connection to occur. Wifi is an important aspect of our everyday life, especially as college students. Current science and technology are constantly looking for ways in which to improve the things we already have. Our project begins to do this in the way that we analyze wifi signal and strength. With the acquired knowledge, we hope to elucidate to the rest of Vassar’s population of the best place to expect reliability and strength of a network. Even more, interestingly, our project fits perfectly with Vassar Urban Enrichment’s initiative to improve wifi quality on campus. With our data (despite its limitations), they would be able to gain a more quantitative aspect to where wifi improvement should be localized as opposed to their more qualitative approach.

What would you do differently if you had to do this project again?

If this project were to be repeated we would pick more locations for our data. Although our data is extensive as it because it represents some of the more used spaces on campus, it would be more beneficial to the student body if we also investigated the wi-fi signal and strength in more locations such as within residential spaces and more academic buildings. Surveying more locations would expand our data, allowing us to notice trends more clearly, perhaps a certain area on campus gets better wifi signal than others or maybe dorms have the best signal of all because it’s where students are expected to spend most of their time. It would also be advantageous if we used equipment that measured the data on the same scale. This way, we would not be observing essentially two different variables, but instead, we could accurately compare and contrast power and strength on their own, independently. Another variable that we would change if we had to redo this project would be to control more variables. We would primarily try to control time by taking data at all locations at approximately the same time to ensure that our data is as consistent as possible. By taking data at around the same time of day, we could compare how the signal varies only by location since perhaps the time of day affects it because certain spaces are more occupied at different times.

What would you do next if you had to continue this project for another 6 weeks?
If we found a correlation between the two variables, we would be interested in creating a mathematical formula that explains the correlation. Further, we would look into examining more correlations or the lack thereof. Another six weeks would allow us to use different equipment in order to find other relationships that correspond to wifi strength and signal. Most, importantly, another six weeks would provide us with a way to decrease variability. This would be done through the use of more data points as well as other locations. This way, we could be more confident in the results that we’ve gathered and the correlations observed. Finally, we would look into collaborating with Vassar Urban Enrichment and their initiative to improve wifi quality on campus.   
By Brenda Dzaringa, Esperanza Garcia, and Anya Scott-Wallace

Description

“The Water Paradise at Vassar” is a project under the supervision of Kevin Fernandez and Issai Torres. We collected samples of water from water fountains in various populated locations at Vassar College and analyze which water fountains is the most drinkable by comparing ph levels and turbidity (water clarity) measurements.

Predictions

The outcome we expected is that water quality will depend on how recently the building’s water system has been installed or renovated. Therefore, we expect the Bridge of Laboratory Sciences or Davison House to have the highest quality of water because it is the newest and renovated building on Vassar’s campus while older buildings such as Thompson Library or Taylor Hall will have a lower quality.

Technology

This team will use the turbidity and pH meter to collect data. The pH strips are responsible for detecting the potential of hydrogen that is inside of a substance which is important to determine the quality of the water. Finding the correlation between the water pH levels from Vassar’s water fountains and favorable levels (What are favorable levels?) of pH for humans is also important to determining water quality. The second equipment is turbidity sensor which measures water clarity by how much light is dispersed when shown through the water.  The use of these two methods of water quality measurement will allow us to gather data to compare water quality across the campus of Vassar.

pH Sensor

pH Sensor Procedure

Our procedure to measure the pH levels of the water from the water fountain was by connecting the pH sensor to the LabQuest and recording data. The pH sensor is initially placed in a solution called the buffer where it would not be affected by any outside particles. When the pH sensor was removed from the buffer, it had to be cleansed with deionized water. Then we placed the pH sensor into a vial containing water from the water fountain and we would record the pH measurement that appeared on the LabQuest. Afterwards, we had to once again cleanse the pH sensor with deionized water and place it back into the buffer. We repeated this procedure for every water fountain we recorded data from.

Data of pH

Explanation of pH

The pH scale ranges from 0 to 14 with 0 being very acidic, 14 being very basic (alkaline), and 7 being neutral. pH itself stands for “power of hydrogen” and is dependent upon the hydrogen ion concentration inside of a substance. The pH scale is logarithmic meaning that a pH level of 5 is 10 times more acidic than a pH level of 6. Pure water has a pH level of 7 and water systems range from pH levels of 6.5 to 8.5. Our data shows that Vassar campus contains good pH levels of water campus wide with the lowest pH level being 7.12 in the New England building and the highest pH level being 7.57 in the ACDC. Our original hypothesis was that Thompson Library or Taylor Hall would have the highest pH level because it is the oldest building on campus and that the Bridge for Laboratory Sciences or Davison House would have the lowest pH levels as it is the most recent building but we weren’t completely right. In conclusion, Vassar College has great levels of pH coming from the water fountains.

Turbidity Sensor

Turbidity Sensor Procedure

Our procedure to measure the turbidity of the water from the water fountain is by connecting the turbidity sensor to the LabQuest. The data is automatically presented with the units NTU, which stands for Nephelometric Turbidity Unit and measures scattered light at 90 degrees from the incident light beam. The light used is white. We calibrate the sensor to 0 NTU, yet it starts with 670.0 NTU. The second step filling up the small container that comes included with the turbidity sensor to the white line. Before we place the container inside the sensor, we must clean the outside of the container with clean paper towels in order to for no excess of water on the surface, which might affect our data. We need to make sure that the turbidity is placed still on a flat surface because shaking the sensor will severely affect the data due to the water particles moving at a fast speed and the light being shaken. Now, we can place the water sample into the sensor and we wait for one minute and thirty seconds in order for the measurements to be accurate and moving between a .1 NTU difference. In addition, we do three trials in total in every location in order to compare the data and find an average. We might test the same water three times or find three different water fountains depending how many water fountains are in the location.

Data of Turbidity

Explanation of Turbidity

The explanation of the turbidity is really crucial. The turbidity measures the quality of water by measuring its transparency and see how clear or how much stuff is in the water. What causes turbidity is phytoplankton, water pipes, sediments from erosion, resuspended sediments from the bottom, waste discharge, algae growth, and urban runoff. In other words, the NTU should be really low in order to drink from it. As you can see from the data table, Taylor Hall has the highest turbidity with an average of 17.67 NTU while Davison House has the lowest with a 1.60 NTU. What I researched is The World Health Organization stated the the turbidity of drinking water shouldn’t be more than 5 NTU, and should ideally be below 1 NTU. Overall, Vassar College has a decent clear water quality.

Reflections

Most of our predictions were right, except the Bridge for Laboratory Sciences being one of the cleanest water sources. Our predictions were based on how recent was the building’s last renovation because that means the building has new pipelines, which can lead to cleaner water. What might have lead to the Bridge for Laboratory Sciences not being really clean might be due to errors in our data. In addition, Davison House was a top choice because it is the most recently renovated dorm at Vassar College. It was built in 1902 and renovated in 2009.

The science we learned during this project is related to the potability of water depending on its clarity and pH levels. Water clarity is important to its potability as it is an indication as to how much particles are in the water that you may drinking when there shouldn’t be any. Water should ideally be below 5 NTUs (Nephelometric Turbidity Units) and at Vassar, that limit is sometimes exceeded in certain buildings. We also learned about pH levels and how for water, they should ideally be close to a pH level 7 and range from 6.5 to 8.5. After gathering pH levels across Vassar, our data shows that Vassar has ideal pH levels for water. The science we had to learn for the pH sensor was what pH stood for “potential for hydrogen” and how that can affect water taste. Overall the science we learned was self taught and it was engaging because of our project.

Our project fits in with current science/technology as it is important to properly identify clean sources of water. There are areas around the world that do not have access to clean water and learning to identify sources that can affect pH levels or turbidity levels of water can be beneficial to helping make access to clean water widespread. Researching water quality also supports the need for other methods of keeping water clearer and safer to drink.

What we would have done differently in our project is be efficient in the time we take to collect the data. The progress was long and tiring, so we would have planned a route using the Vassar Campus Map and see which route is the fastest. Also, we could have calibrated the turbidity sensor and pH meter after every usage, but we did not have enough time to do it.

If we had more an additional six weeks for this project, we would have test every water source at campus from bathroom sinks to kitchen sinks and water fountains. Also, we would have tested all of our data again in order have more accuracy. Our research would have contained more details about pH levels and turbidity in order for our audience to have a better understanding of what the water is different in many locations at Vassar College.

Introduction

I chose this project because I noticed how often I had been using my speaker for activities on campus. More often than not, my flat mates would use it to enjoy some music while making dinner, or I would be tasked with supplying the music for a party. Either way, I saw that I was getting a considerable amount of mileage out of my speaker, and became interested to see how much electricity I was drawing with such a loud yet compact machine. My project sought to determine the loudness, measured in decibels, and power consumption, measured in watts, of my speaker and how power consumption is affected as the speaker outputs music at louder volumes. To do this, I used equipment to measure the wattage of my speaker, and a phone app to record the decibels produced. I used a standardized sound clip to make sure the data was consistent across all trials, with each trial being a different level of volume.

Data Interpretation

The graphs were made in Excel using data collected. The data for wattage was collected with Logger Pro, obtained through a free demo, and the Watts Up Pro, obtained through the physics department. The data for decibels was collected using an android app called “Sound Meter.” I collected the data through Logger Pro and copied it over to Excel. Each round of data collection consisted of setting the speaker volume at a certain level, then measuring wattage with the Watts Up and decibels with Sound Meter as I played the first 10 seconds of “Day & Night” by Thundercat. I chose a short song in case I wanted to play through its entirety. The data shows a steady increase for both decibels and watts, however this increase is much smaller than I originally thought. It seems the speaker is able to efficiently use power, as louder volumes increase the wattage very little. Throughout the experiment, the difference between the lowest and highest wattage used is less than 1 complete unit(not counting when the speaker is off). As for decibels, although there was a consistent increase as volume increased, the data stayed in the same general area for each of the measurements for min, average, and max dB. Upon further research I discovered that decibels are a logarithmic unit. Because of this, loudness is not measured in a linear manner. For example, an increase of 10 decibels would mean that a sound is now twice as loud as before.

After researching electricity providers in the Poughkeepsie area, I was able to determine that electricity sells for about $0.073 cents a kWh. I did some calculations using these numbers to interpret the difference in cost from electricity use in playing my speaker at different volumes. Because the difference in wattage and decibels between individual levels of volume is so incrementally small, I found it more illuminating and satisfying to simply use the measurements of the highest and lowest(without being off) volumes. The highest volume had an average loudness of 80 db, with an average power use of 6.29 watts. The lowest level had measurements of 50 dB and 6.08 watts, respectively. In order to have rounder and more intuitive figures, I scaled up the time in the following measurements from 10 seconds to 1 month. If I were to play music through my speaker for an entire month at the loudest volume, I would spend $0.33 on electricity. If I did the same at the quietest volume, I would spend $0.319. The difference in loudness between the highest and lowest volume is 30 dB. So, the difference in rate divided by the difference in loudness gives the total cost difference of playing my speaker at different volumes. This comes out to be an increase of $0.0007 per 1 dB increase.

Discussion

I learned during the course of the experiment the scaling of loudness when measuring in decibels. Since most of the exposure to measurement units we have in our everyday life is linear, it’s a bit unnerving when encountering a logarithmic unit. In relation to current science, it’s interesting to see how the electronics we use everyday consume power. There’s push for energy policy changes and understanding how much energy we use and how is an important part of making those decisions. If I had to do this project, I would invest in a better loudness measuring device. The app on my phone was accurate enough, but having consistent measuring through a more reliable device would have made data gathering easier. If I had to continue this project for another six weeks, I would test the power consumption over longer periods of time, as well as utilizing other different speakers to see how much power is used by different brands at comparable loudness.

Results:

Explanation of Results:

The results in the above graph show the average dB levels for each condition. The line across the center of the graph shows the mean dB level of all trials, 66.59 dB. The standard deviation from this mean is 16.439 dB.

The vast majority of the conditions we tested do not pose a threat to our hearing. Sound during lectures, during meals, from computer speakers, in our rooms, and in the library was not found to be harmful. Even while working in the Vassar Infant Toddler Center,  surrounded by crying babies, there seems to be very little danger. However, some of the sounds recorded were loud enough to eventually cause hearing damage. According to the National Institute on Deafness and Other Communication Disorders and to The American Speech-Language-Hearing Association, repeated or prolonged exposure to sounds at or above 85 dB can cause damage to, or death of hair cells. Hair cells are sensory receptors of the auditory system, in the cochlea. Damage to hair cells often results in hearing loss.

The average amplitude of the Villard room party we measured was 93.8 dB. According to the Center for Disease Control and Prevention (CDC), repeated exposure to this amplitude for under two hours could be dangerous to hearing. The sound intensity reached as high as 101.5 dB in the Villard room party. According to the CDC, repeated exposure of just 15 minutes at a time can cause damage when the amplitude of the sound is at 100 dB. This is to say that going to Villard room parties repeatedly over your time at Vassar, could cause permanent hearing loss.

We tested the intensity of sound that comes out of headphones and earbuds multiple times in the project. When listening to music at 100% volume from a headset, the mean amplitude was only 60.86 dB, which does not pose any threat to hearing, even after long exposure. Listening to music at 100% volume from Apple earbuds, the mean amplitude was 83.39 dB and the intensity went up to 91.48 dB at some points. Over years, these intensities can damage ears after repeated exposure of just a few hours a day. Apple earbuds have holes on the back that let some of the sound escape from them. They are made to lower the likelihood of causing damage to your ears. For one of our runs, keeping the volume constant, we covered these holes and found a mean amplitude of 91.46 dB and a high of 101.9 dB. The mean amplitude of the sound from the covered earbuds was essentially the same as the highest amplitude emitted from the uncovered earbuds. The highest amplitude for the uncovered earbuds run was high enough to cause damage after exposure of less than 15 minutes a day, according to the CDC. We also tested another brand of earbuds, JVC, that do not have holes on the back to release sound. The mean amplitude was 90.66 dB and the highest was 97.23 dB. These values were higher than the sound levels we measured from untampered Apple earbuds, and only slightly lower than the intensity measured when the Apple earbuds were covered. This indicates that the holes on the back of Apple headphones do in fact work to protect listeners from hearing loss.

Another potentially hazardous source of sound we are exposed to is from musical instruments. We measured the sound emitted from an oboe, and found a mean amplitude of 91.29 dB and a high of 101.40 dB. Over a few years, exposure to these sound levels for even less than 2 hours at a time, can cause permanent damage. This is important to note because people who play instruments often have 2-hour long rehearsals, and have to practice by themselves on top of that.

Somewhat surprising to us, was that the ACDC at dinner time reached sound levels of 91.31 dB. The mean amplitude was only 79.9 dB, which is not damaging, but the sound did get intense enough to cause some damage over extended periods of time. Considering that many Vassar students eat at the ACDC every night for months, this is an interesting find. According to the CDC, repeated exposure to 90 dB for even less than 2 hours at a time can cause hearing damage. The data suggests that the sound fluctuates enough that no student would be exposed to 90 dB of sound for an entire 2 hours at the ACDC. However, it is something to keep in mind on especially busy ACDC nights.

Expectations:

Our results were for the most part as predicted. For example, we did not expect quiet places, such as the library or our own rooms, to be loud enough to cause hearing damage; we wanted to study them for comparison. We expected the sounds at the Villard room party to be intense. However, we did not realize how damaging they would be. As explained above, repeated attendance at these parties could cause permanent hearing loss. We expected the sound emitted from headphones at a high volume to be enough to damage ears, because this is one of the main warnings you are given when told about hearing loss. However, we did not realize the difference that different types of headphones/earbuds would have on our measurements. The same song was played at the same volume through different earbuds, and resulted in different amplitudes.

Problems that arose:

It is important to point out the limitations of our study. We were only able to measure most conditions one time and the data would be stronger if the measurements were repeated. We also had difficulties when measuring the sound emitted from headphones/earbuds. We held the microphone up to the speakers, in an attempt to imitate the placement in relation to our ears when we are actually listening to music. However, in actuality, part of what makes headphones/earbuds so dangerous, is that the sound is tunneled through the ear canal to the inner ear. We were not able to recreate this, and some of the sound escaped during our measurements. This would be an interesting problem to attempt to solve. Possibly a model of the human ear canal would be needed to take accurate measurements of which sounds are really reaching and damaging hair cells.

Take away message:

In order to prevent hearing loss while at Vassar, students can limit their prolonged exposure to Villard room parties and limit their proximity to those practicing loud instruments. Additionally, we have observed the effect of tampering with headphones, and demonstrated the importance of using earbuds as intended, and at moderate volumes. Investing in a pair of headphones that allows sound to escape may be beneficial, as would be keeping them in their original condition.

Science we learned:

Although we already knew about sound amplitude and decibels, through the project we learned the significance of these measured values. We learned that 30-40 dB is very quiet while 85+ dB can be damaging over time. We also learned how to use a Sound Level Meter (SLM), which we used to take our data. By playing with the different SLM settings in order to figure out which to use, we learned more about it. For example, we could either record continuous measurements of fluctuating sound, or just record the maximum values, depending on the setting. We also learned that different settings are needed to measure lower amplitudes versus higher ones. We learned that the SLM has a microphone that senses and records sound. When connected to the LabQuest 2, the data resulting from the recorded sounds was displayed as a graph. We could then connect the LabQuest 2 to a computer with Logger Pro to further analyze the sound.

Additional data we would have liked to look at:

If we could have done this differently, we would have also tried to record the frequencies of the sound waves. With our limited amount of time, we were only able to obtain the amplitudes of the sound waves. We would have also liked to note how often an average person is exposed to these sound levels and for how long. We had some events that were extremely loud that many students only attend once a month, so the effect of these occasions may seem insignificant in the grand scheme of things.

The Next Step:

If we had another six weeks, we would have taken a lot more data. Particularly, we would try to have a larger variety of data, but also enough points for each activity to get a good average for each activity. We would have also liked to calculate how long the exposure to a certain activity had to be to damage our ears.

Citations:

“About Hearing Loss.” CDC. n.p., n.d. Web. 25 Feb. 2014.

“Noise.” ASHA. n.p., n.d. Web. 17 Feb. 2014.

“Noise-Induced Hearing Loss.” NIDCD. NIH, Oct. 2013. Web. 17 Feb. 2014.

What were your results?

After conducting the appropriate calculations to take into account how often each of these appliances is actually on/in use versus simply plugged in (for a typical TH), we found that the total cost of powering all of these personal appliances based on typical usage in a semester would be $69.95. This is considering that there are 5 bedrooms in the house so we have multiplied the bedroom costs by 5. Below is a graph depicting the energy consumption by rooms, which demonstrates that the majority of the energy consumption comes from the 5 bedrooms.

To provide a contrast, the cost of powering all of these appliances if each of them remained in use for the entire semester would be $1,253.83. Clearly this is not a realistic scenario, but the extreme disparity between the numbers helps provide a context to better understand the realities of our calculated energy consumption. The graphs below depict the cost ($) of powering each appliance when plugged in versus in use/on for a semester (4 months) based on a typical monthly usage. The first graph shows the data with a larger scale, and the second shows the data on a smaller scale to reveal the smaller details.

             With regards to energy consumption, the total amount of energy (in kilowatt hours) all of these appliances use in a semester—taking into account how often each of them is actually on/in use versus simply plugged in—comes out to about 3,103 kilowatt hours. (This is also considering that there are 5 bedrooms in the house so we have multiplied the bedroom energy consumption by 5.) The graphs below depict the energy consumption (in watt hours) of each appliance when plugged in versus on/in use over a semester (4 months) based on a typical monthly usage.

             All of these calculations were made based off of what we believed was a typical monthly usage time for each appliance. In the chart below we explain what we believe to be a typical daily usage (minutes or hours) for each for each appliance. (For some appliances that aren’t used every day—such as a vacuum, for example—the typical monthly usage was decided and divided by 30 to find average daily usage.)

Looking at the graphs, it is clear that certain appliances contributed to the majority of the cost and the energy consumption as compared to other appliances. The appliances that consumed the most energy were (from most to least out of all the substantial contributors): the mini fridge, floor lamps, desk lamps, computer charger, fan, Christmas lights, kettle, and microwave. Similarly, the appliances that contributed most to the semester’s cost were (from most to least of the substantial contributors): the mini fridge, floor lamp, and desk lamp. In this case, there is a large difference in cost between the floor lamp and desk lamp, with fairly insignificant values for the appliances after the desk lamp as well.

Knowing that the mini fridge and floor lamps are the main source of energy use and cost can provide students with valuable information when deciding which appliances to have in their households. It is important to keep in mind that the total cost and energy consumption calculated for a typical TH included 5 mini fridges (because each bedroom typically includes a mini fridge), so both of these values would decrease relatively significantly if a house has less than 5 mini fridges.              We must also take into account the fact that we didn’t gather data for the stove, heat, overhead lighting, or main refrigerator, which in future housing (not on a college campus) will likely make most of the impact in an electricity bill and with general energy consumption.

What do your results mean?

Although this is only significant with some appliances, leaving them plugged in when not in use really can make a difference. Even though it is not as much as we originally thought, just the fact that leaving certain appliances plugged in (when not in use) does cost some money and use quite a bit of energy reinforces the belief that most things should remain unplugged when not in use.

Additionally, our data demonstrates that using alternative methods to making certain foods or doing certain activities could make a difference, however small it may seem. For example, one could make popcorn on the stove to avoid using the microwave or a popcorn popper, or one could use a toaster instead of toaster oven. Cost and energy consumption could also be reduced by cutting down on the number of mini fridges in a house, by unplugging Christmas lights when no one is in the room, and especially by turning off and unplugging floor lamps when they are not being used. Even simply cutting down on the amount of time one uses each appliance per day or per month could make a small but important difference for energy conservation as well as saving money. Below we have included some simple pie charts that depict comparisons between certain appliances that have similar functions and could be used as alternatives.

Without knowing the cost of the main appliances (oven, stove, big refrigerator, etc.) it is hard to make any general statements about the portion of our tuition that goes towards housing because the cost of these personal appliances is relatively insignificant in comparison to the cost of the main appliances. However, it is important to be aware of how all the little costs and power usages add up: soon we (college students) will have to pay full electricity bills ourselves, and energy conservation is a crucial part of taking care of our environment.

Were your results as predicted?  Why? or Why not?

In general, our results confirmed our predictions. We expected appliances such as the mini fridge and lighting sources to be the biggest contributors to cost and energy consumption, and this was definitely confirmed. The refrigerator is on constantly and uses a lot of energy to keep it at such high temperatures, and the floor lamps and most lighting sources are on for such a large part of the day that we also expected them to use a lot of energy and contribute a lot of the cost. That being said, a few of the appliances did provide surprising results; we had not expected the Christmas lights, kettle, or the popcorn popper to have values as high as they did, but now that we know more about how these appliances use money and energy, we can adjust and cut down on how often we use them.

What science did you learn during this project?

Despite this being a small project, it was very informative. Not only did it give us some insight into how much energy our appliances use, and the subsequent costs to operate and maintain these appliances, but it taught useful applications of basic science. Because we were measuring energy consumption we have now become adept at using the Watts Up? Pro and can have a better understanding of converting different units of energy such as watts (joules/sec) to watt hours, and joules to watt hours. In addition, we have learnt how these different values of energy consumption relate to the cost of operating an appliance.

What would you do differently if you had to do this project again?

Having now completed the project, we are more aware of some of the sources of error and limitations we faced. If we had to repeat this project we would make a simple graph of watts by time for each appliance. A problem we occurred when doing this project was that some appliance, particularly those whose function was to produce heat (kettle, toaster etc.), varied in energy consumption. This was probably due to the fact that it was using more or less energy dependent on how much heat it still needed to produce. If we had graphed watts by time we could have used this to calculate the average energy consumption during the usage of the appliance. This I believe was the major confound in doing this experiment.

What would you do next if you had to continue this project for another 6 weeks?

If we had to continue the experiment for another 6 weeks, we would widen our sample size and take averages of the energy consumption of the appliances, as well as the reported usage of these appliances by residents. In addition, to ensure more accurate and realistic data we would have a “sample month”, in which we record carefully the amount of time of usage of each appliance in this month. We were restricted in doing this due to the short span of time to conceptualize and carry out this experiment. However, given more time we could have removed a great deal of conjecture from our project.

I. Results

A. Results Regarding Radiation

Overall, all microwaves measured emitted a fairly similar amount of radiation, ranging from the weakest emission at the furthest point from the microwave at 30 µW/m^2 to the strongest emission at the closest point to the microwave at 1,500 µW/m^2.  While the general trend seemed to be that radiation decreased as we moved further from the microwaves, not all cases followed this trend exactly.  To further understand factors that may have affected radiation, we compared radiation with 1) the power levels of microwaves and 2) the age of microwaves.  The following graphs show this comparison, with an added average line to see which microwaves fall below and above the average.  The graphs plot the Average values from the front at 30 cm.  We chose this orientation and distance because we felt it is the most practical in reference to where a person would be standing while microwaving food.  Furthermore, since some microwaves emit a relatively consistent amount of radiation regardless of distance from the microwave, and others taper off, we felt this represented a good middle ground.

i.  Microwave Age

It is certainly notable that the oldest microwave (M4) emitted by far the most amount of radiation.  However, as the years progress, the general trend after that case does not necessarily descend.  A microwave from 2011 also emitted a significant amount of radiation higher than the average.  It is also notable that when taking measurements of the 1999 microwave, the only industrial microwave in our sample, the radiation emitted seemed to appear in cycles.  It would drop down to zero, rise consistently, then fall back to zero.  This cycle made it difficult to choose an average from the reader, and also perhaps accounted for our perceived higher average radiation.  While microwaves may have become more advanced over the years, therefore emitting less radiation, we would need a larger sample and to keep power levels constant to test this hypothesis further.

ii. Microwave Power

The association between power, in Watts, and electromagnetic radiation seems to be a positive one.  The microwaves that, on average, emitted the most radiation also were the highest in power, exceeding the average.  The microwaves that emitted radiation below the average were lower in power.  The exceedingly high spike in EM radiation in the 1250 Watt microwave may be influenced by other factors, considered in section i., but is significant nonetheless.  While again we would need a larger sample and more controlled conditions to test for a correlation between these two variables, there does seem to be a positive relationship. 

This microwave, M4, was the oldest microwave in our sample and also the only non-commercial microwave in our sample, as evident from its unconventional aesthetics.  While it emitted by far the highest amount of radiation, it provided an interesting case to investigate further.

B. Microwave Radiation and Safety Standards

The EM radiation data values were all significantly below the safety standards set for consumer microwaves.  (See Section II.)  Across variables of age, power output, wear and tear, and added interference, no microwaves at any point even exceeded half of the safety limit set by the United States Federal Food and Drug Administration.

C. RF Meter Findings

Through our data collecting process, we also went through trials and tribulations with the RF meter, an instrument used to measure EM radiation.  Since the manual was relatively vague, we performed a lot of trial and error to get the most accurate measurements possible.  We had a few helpful findings that may be helpful to individuals using this instrument moving forward.

First, we found it is necessary to take a preliminary measurement of EM radiation in the general vicinity of the appliance being measured.  This interference may account for unforeseen variance and unexpected values in a data set so it is good to know if it exists or not.  Furthermore, it is important to keep nearby cell phones and laptops off, as they can also interfere with these measurements.

Second, we found it more accurate, in our case, to measure from one axis rather than all three.  This limits interference from other directions, and therefore leads to a more accurate measurement of the appliance itself.

Finally, we found it important to use different settings of the RF meter to measure different values.  While we began measuring just on the “Maximum Average” setting, we soon realized that this was an unreliable measurement for getting a sense of the general radiation emitted.  Furthermore, the highest calculated “Maximum Average” value remains on the RF meter until a higher radiation is detected.  Therefore, if something interferes for even a second, its value will be displayed and remain displayed on the RF meter.  We decided that although this value is telling, we also needed a more reliable, general idea of emission.  We decided to use the “Average” setting for this, which averages the values every few seconds, and displays that reading.  Since the reading constantly changes, we watched the meter in pairs and decided a number that seemed to be a middle-ground of the readings we observed.  These settings are important to test and understand so that the operator is truly measuring what they are meaning to measure.

II. Results Analysis and Conclusions

The process of generating high levels of heat through the use of microwaves does mean that contact with human tissue and organs is potentially lethal. Despite this, there are few health risks posed by common consumer microwave ovens due to strict safety standards and efficient interlocking technology.

First, the International Electrotechnical Commission has set a standard of emission limit of 50 Watts per square meter at any point more than five centimeters from the oven surface. The United States Federal Food and Drug Administration has set stricter standards of 5 milliWatts per square centimeter at any point more than two inches from the surface. Most consumer microwaves report to meet these standards easily. Further, the dropoff in microwave radiation is significant with the FDA reporting “a measurement made 20 inches from an oven would be approximately one one-hundredth of the value measured at 2 inches.” As the majority of our readings, despite substantial electromagnetic interface at times, were in the microWatts range these standards appear to be successful.

Second, microwaves use a two-step interlock system that ensures the magnetron cannot function while the door is open. This means little radiation leaks, and opening the door even when the oven is turned on will immediately shut off all microwave radiation emission. Our readings did suggest higher levels leaked from the right side of the oven (near the magnetron) than from the door, but these levels remained well below international standards.

Our results are not overly surprising as we entered the experiment recognizing the strict safety standards in place for microwave oven radiation levels. Thus, our data supports our hypothesis: standard consumer microwave ovens do not emit microwave radiation levels anywhere near levels needed to be dangerous to the user. While not all of our data is as logical, when graphed, as expected, we believe this to be a result of our imperfect data taking conditions and irregular interference levels. Should we continue to record data in more controlled conditions, we believe the outcomes would continue to adhere to safe standards.

III. What Science Did We Learn?

Microwaves are high frequency radio waves used for many purposes from television broadcasting to kitchen cooking. Microwave ovens are common household items that generate microwaves (around 2450 MHz) using a metal tube called a magnetron. These microwaves are directed into the oven cavity – a space of metal walls, roof, and ground with the exception of the oven door. Metal totally reflects microwaves, creating high bounce back in the oven, while glass and some plastic is nearly transparent to microwaves, allowing the waves to be readily absorbed into food (especially those largely water based). Microwaves force atoms to reverse polarity at high enough rates to generate heat and, thus, cook the food or boil the water.

While the radiation of microwaves can be dangerous, microwave ovens adhere to safety standards that prevent harm with proper use and maintenance (if an oven door is damaged, more radiation may leak out). While microwaves have been shown to break down key nutrients in some food, the process does not radiate the food or make it dangerous to eat, only less healthy.

IV. For the Future…

If we had to do this project again, we start by testing the RF meter and its functions before gathering data with it to gain a better understanding of its diverse (and sometimes unintuitive) settings (Max Avg vs Avg, etc etc). We collected some surprising data from the industrial microwave (M4) tested; the radiation levels fluctuated from almost nothing to nearly 2.5mW/m2 (Max Avg), which is a huge range! Perhaps this was partially caused by the base-level radiation (this was the only microwave whose surroundings had a measurable electromagnetic field without being on), perhaps we didn’t have a complete handle of the RF meter, or perhaps the microwave functioned in a different way from the others, sending out pulses instead of a steady stream of microwaves and so creating the oscillation in our readings. Should we do the project again, we would make sure we knew precisely how all data the RF meter takes is taken, and we would research further the different mechanics of microwaves to better explain surprising data such as this.

V. Next Steps

If we had to extend this project, we would test a wider variety of microwave models: it would be interesting to test the trend of microwave emission over the years, gathering data and testing a hypothesis concerning the technologic improvement being made in microwave development.  It would also be interesting to test industrial microwaves versus commercial microwaves, seeing as how M4 differed so greatly from the other microwaves.   We would also be sure to widen our sample selection to more reliably test some of the relationships we have preliminarily identified.  While the relationship between microwave power output and EM radiation seemed promising, we would need to test this hypothesis in a bigger sample, with more controlled conditions, to find a mathematical formula to describe this relationship.

Emma Foley; Hunter Furnish; Hannah Tobias

For our research project, we attempted to measure the counts of radiation in academic buildings around campus using a Geiger Müller (GM) tube attached to a LabQuest 2. We were also interested in seeing if the radiation levels observed correlated with the ages of the buildings tested. This is an important type of testing to do, as over-exposure to radiation, especially particles, which are high energy photons without mass, can lead to negative results. These can include radiation poisoning, as well as cancer and other genetic mutations. To conduct our research, we walked around each of the buildings at a steady pace for 5 minutes, moving the GM tube from side to side. When there was an indication of possible radiation contamination, the tube was focused on that area to determine if there was a higher radiation count.  For example, there are areas in Olmstead that have radiation warnings on the door, and we stopped and waved the Geiger tube there for a considerable amount of time to test for any radiation contamination that may have been leaking through.

Figure 1. The apparatus used for recording radiation. The GM tube is located on the right. It is a gas filled detector, which functions using a low-pressured inert gas to amplify the signal of any radiation entering the tube. Radiation passes through the gas in the device and the molecules in that gas are ionized, leaving positive and negative ions in the chamber. These ions move toward separate charged sides (the anode and cathode), creating a current which is then sent through the wire to the LabQuest 2 Device to be measured and recorded. Each , , or particle entering the tube is measured as one “count” of radiation.

Figure 2. Table of Average and Maximum radiation counts as compared with the age of the building. As read from left to right, the columns are labeled as (1) the buildings tested, with “Background” representing the data we collected between buildings to determine an average radiation level, (2) the average count of radiation observed in each building (per 0.1 of a minute over the course of 5 minutes), and (3) the highest amount of radiation observed in each building, and the age of the buildings that we observed. We initially hoped to be able to distinguish , , and radiation from each other, but upon further review, we determined the only types of radiation we were likely to detect were and high energy . This is because these travel further from their source than , and are generally emitted by the same type of material.

Figure 3. The average radiation counts compared with the age of the buildings. A trend line has been plotted to show the direction of correlation. The black line indicates the linear regression line of best fit, and the blue lines represent the upper and lower limits of the possible fit of that line, according to the standard deviation of the data.

Figure 4. The maximum radiation counts compared with the age of the buildings tested. A trend line has been plotted to show the direction of correlation. The black line indicates the linear regression line of best fit, and the blue lines represent the upper and lower limits of the possible fit of that line, according to the standard deviation of the data.

We plotted the above data observed in two graphs (Figures 3 & 4).  Figure 3 shows the average radiation levels by the year that the building was built, while figure 4 shows the maximum radiation level observed by the year the building was built.  According to the statistical testing, there is hardly any correlation in the data for either graph. In figure 3, r=0.275 and r²=0.076, and in figure 4, r=0.228, r²=0.052, where the “r” value indicates the closeness of correlation of the data, and the r² value indicates the percent of data that fits within that correlation. Since both are rather close to zero, this indicates very little fit in the data. Even so, the standard deviation of the average radiation values was only 0.41, which makes the range of possible best fit lines less than half a point higher or lower on either side of the already plotted line, and the maximum radiation level, although a bit higher, has a standard deviation of only 0.95, which still would only raise or lower the line of best fit by less than one count of radiation on either side of the already plotted line. Considering the already low levels of radiation, this standard deviation does not influence the significance of the data in terms of dangerousness of radiation.

The literature provided by Vernier, the makers of M tube and the LabQuest 2 device, states that expected background radiation levels should be between between 0-2.5 counts of radiation/0.1 min. Our average background radiation testing was within this range (avg=1.32 counts/0.1 min, max=3 counts/0.1 min). All of the average readings from buildings were also within this range (the highest average being taken in Skinner Hall: 2.44). Since the radiation count values are so low, and the statistical analysis does not indicate a high possibility that radiation levels are out of our tested range, we can conclude that Vassar campus is safe in terms of radiation levels.

What would you do differently if you had to do this project again?

If we had to redo this project, we would have monitored radiation levels in relation to the GPS coordinates of the buildings.  This would have allowed us to find a possible association between locations on campus and radiation levels. While this would have also more than likely ended up manifesting in insignificant results, it is possible that we could have found an interesting relationship between the two.  It is definitely possible that certain areas of campus are more radioactive than other areas of campus.

What would you do next if you had to continue this project for another 6 weeks?

If this class were to continue for another 6 weeks, we would have been able to attempt to differentiate between types of radiation detected by placing a few sheets of aluminum foil in front of the detector. Only radiation should be able to pass through this barrier, and the other types of radiation should not. We would certainly have tested this with materials we knew to be radioactive before we went into the field.  The data we collected with the Geiger tube did not differentiate between types of radiation.  This could be somewhat problematic.  Certain types of radiation (i.e. and low-energy ) are much less harmful to humans than other types of radiation (i.e. high-energy and ).  By knowing what kinds of radiation we are detecting, we could have more information about the potential risks facing the Vassar community.

What science did you learn during this project?

First of all, we learned about the purpose of the Geiger tube and how it works. This is explained earlier in this post.  We also learned about the different types of radiation, and the risks associated with each kind. radiations are short range particles that  are made up of helium-4 (4He) nuclei. They pose little external hazard. radiations are lighter short range particles made up of either electrons or positrons that can pose some risk, but are easily stopped by barriers as thin as a piece of paper. radiations are photons traveling at high speed that can cause major damage to DNA and other chemocellular functions. These are not easily stopped. Finally, we learned about compiling our data into concise and succinct data tables and graphs.

Information from an Interview with Professor Dave Jemiolo

Dave Jemiolo is the current radiation safety officer on Vassar’s campus, as well as a professor of Biology. We spoke with him about his experience dealing with an issue of radiation in Sanders Physics that came up a few years ago.

Jim Kelly, the radiation safety officer at the time, asked Professor Jemiolo to check out a darkroom below the auditorium in Sanders Physics. By using a geiger counter, he discovered that the entire floor of the room was hot with Radium contamination. He left x-ray paper overnight on the hottest parts of the floor and, upon review, saw that radiation had leached into the paper at various points. It seemed that a radioactive substance had been spilled on the floor, probably in the 1940s, and then some of it was unwittingly sealed in with varnish. He called in some specialists from off campus who ripped out the floor of the room. This led to the physics library below, where Jemiolo discovered background levels of radiation 3 times higher than normal in the entire room. Upon inspection, he discovered that the chemistry department had stored chemical compounds on shelves at one end of the room. Because they were alphabetized, elements like Thorium and Uranium were placed closed together. These two elements are natural radiation emitters, but had never been on license at Vassar before that point and were leaching radioactivity into the room.

In another instance, Professor Jemiolo was asked to check for radiation sources in the geology department. He suspected that radiation could be coming from naturally radioactive minerals stored there, in much the same way as those he discovered in Sanders Physics. He was right and prompted the removal of various minerals stored there. In an exciting turn of events, after removing radioactive minerals from a box and then removing the still hot box, he found radiation seeping through a wall. It was coming from a large rock of Uranium (oxide) that was radioactive enough to penetrate a solid wall.

What these two stories point to is the fact that not all radiation exists as we may imagine. There are many elements where radiation naturally occurs. Professor Jemiolo showed examples of this in one of the Biology labs, including potassium (one of its isotopes is a weak beta emitter).

Many things we are around on a daily basis emit radiation. Older clocks used to have their dials coated in a paint containing Radium because of its luminescent properties. Bananas are rich in Potassium. Some welding rods contain Thorium. This points to some interesting directions our research could have taken. It also is indicative of the many ways in which we are exposed to radiation on a daily basis, but at levels our body is usually capable of regulating or that do not pose a threat.