The goal of my project was to explore a relatively well understood model for light scattered off spherical particles in the interstellar medium (ISM): Mie theory. Over the course of my investigations I switched my inquiry from attempting to derive and plot the asymmetry parameter, g, to plotting the extinction efficiency $Q_{ext}$. Note: I have included portions from my preliminary data post in order to maintain clarity and continuity. Portions from the preliminary post are still relevant and will remain likewise.
Final Reflections
An important question emerges in the study of scattered light in the interstellar medium (ISM). Why use the Mie solutions to Maxwell’s equations as opposed to the Rayleigh or Debye methods for modeling this scattering? As with many other methodological decisions, the answer lies in the physical parameters and observational requirements of the system that I’m trying to model. Optical observational data of extinction due to dust grains as a function of wavelength is denoted by: $A_\lambda$ and this observed data necessitates that the extinction be inversely proportional to wavelength:
$A_\lambda\propto\lambda{^-1}$
i.e. the wavelength must be approximately the size of the grains in question. Only with that dependency will the the model fit the data. Wavelength dependencies for Rayleigh and Debye scattering do not provide the necessary proportion.
Asymmetry parameter, g
As indicated in my preliminary data, modeling the Mie solutions to Maxwell’s equations for scattered light by spherical particles has proven tricky. Ultimately my attempt to plot the asymmetry parameter, g, was unsuccessful, but I was able to plot another grain property instead, the extinction coefficient $Q_{ext}$, versus dimensionless size parameter x (which I will explain in a later subsection of this post). My Mathematica code for the asymmetry work is attached at the bottom of this post as it was in the preliminary data post, but I updated the notebook since I commented on those results and have concluded that work with a derivation of the scattering coefficients $a_n$ and $b_n$.
Below I detail my journey through the asymmetry parameter, g, within of through Mathematica 9 and the processes that comprised those investigations. I find that detailing where I made it up through is important in the process of fixing my work in the future, in addition to being a pedagogically useful process (learning through mistakes!).
I made some simplifying (and yet physically relevant) assumptions. The spherical grains will be water ice with an index of refraction of n=1.33. The vacuum will have an index of refraction of n=1. Items [k, 1] and [k, 2] are coefficients for the imaginary portion of the indices of refraction. I have assumed a wavelength within the optical spectrum. [K, 1] – [K, 3] are the wave numbers for the different indices and included are the wavelengths necessary to derive those wave numbers. Lastly I have provided an arbitrary, placeholder grain radius.
I have also defined grain size parameters, necessary for the calculation of the coefficients $a_n$ and $b_n$, shown below.
Helpfully, Mathematica has Bessel functions built in. I used them in my exploration into modeling the asymmetry parameter. Dependent on interstellar grains properties, i.e. if it’s dielectric and thus has a real index of refraction or it has a complex index of refraction (impure water ice grain), the Bessel or Ricati-Bessel function will change.
Lastly, here’s my code for the coefficients, $a_n$ and $b_n$. $\alpha$ and $\beta$ have been replaced with q, but those values are still the size parameters.
$Q_{ext}$ v. Size Parameter
In exploring scattering within the interstellar medium (ISM), it is possible to define an extinction efficiency $Q_{ext}$. This efficiency is dependent on index of refraction, m, and can be approximated by
$Q_{ext}\approxeq(8/3)x^4|{\frac{m^2-1}{m^2+2}}|^2$
where $x=2\pia/\lambda$ and is the dimensionless size parameter, depending on grain radius, a.
In Mathematica I began by defining a wavelength (red light in microns) and the indices of refraction. Note that indices $m_2$ and $m_3$ (denoted by d2, d3) involve complex components. These components are necessary because of the nature of the grains, which in this case I assumed to be made of different ices.
Next I defined the size parameter, $x=2\pia/\lambda$ as well as interior terms for the $Q_{ext}\approxeq(8/3)x^4|{\frac{m^2-1}{m^2+2}}|^2$ equation; specifically, I define ${\frac{m^2-1}{m^2+2}}^2$.
Next I combined the previous bits of Mathematica code to get the actual values for $Q_{ext}$
and then applied a transpose on my data points (where x-values need to be the size parameter, x, and y-values need to be $Q_{ext}$) to be able to ListPlot the three $Q_{ext}$ v. size parameter plots. Transposes shown below!
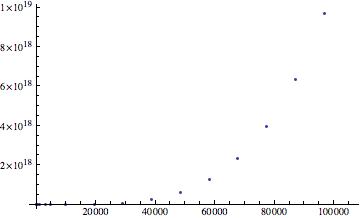
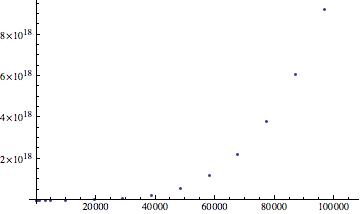
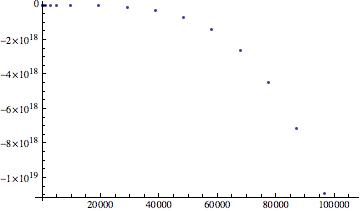
Now I could create my plots! Note that the scales are arbitrary, what I am interested in is the behavior of the plots. This behavior dictates differences in ice grain extinction efficiencies dependent on size and index of refraction. Below are my three plots:
Qext v size parameter x (m = 1.33)
Qext v size parameter x (m = 1.33-0.09i)
Qext v size parameter x (m = 1.27-1.37i)
Conclusion
While the plots for Qext v size parameter x for m=1.33 and m=1.33-0.09i show a positive exponential trend, the final plot shows quite the opposite behavior. For grains with indices of refraction that have complex components, extinction efficiency versus size parameter plots should indicate a damping in the plot. So I do have some confusion with my plots. The third plot clearly indicates a variation in behavior when compared to the first two, but the second plot (of an extinction efficiency involving a complex index of refraction) should behave similarly to plot 3, not plot 1. This is a good transitioning point into where this work could go in the future – examining whether or not the extinction efficiency versus size parameter plots were indeed done correctly. Mathematica is lenient neither in syntax nor its learning curve! In the future it would also be useful to try and continue my work on the asymmetry parameter, but that might take a greater commitment than just fixing what may be incorrect with the extinction efficiency plots.
I have learned a great deal over the past few weeks about research and computational modeling. I have truly grown in respect to my appreciation for modeling and all the hiccups and hurdles that come with learning how to effectively and efficiently use Mathematica. While my explorations into the asymmetry parameter, g, were unsuccessful at producing a plot, I am very proud at being able to produce plots of extinction efficiency $Q_{ext}$ versus size parameter, x. The results, while not ideal, still reflect trends in the physical behavior of the system – in this case the light scattered by spherical particles in the interstellar medium (ISM).
Resources
- Introduction to Electrodynamics, 4th ed. by David J. Griffiths
- Physics of the Galaxy and Interstellar Matter by H. Scheffler and H. Elsässer
- Interstellar Grains by N.C. Wickramasinghe
- Physical Processes in the Interstellar Medium by Lyman Spitzer, Jr.
- The scattering of light, and other electromagnetic radiation by Milton Kerker
- Mathematica 9 Help Documentation Center (the most valuable resource!)
Mathematica notebooks:
https://drive.google.com/file/d/0B_r-c0PTUHZldHVNREtrWHlzZXc/edit?usp=sharing
https://drive.google.com/file/d/0B_r-c0PTUHZlNVh5emxudUJrRDA/edit?usp=sharing