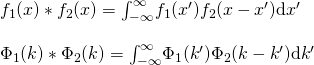Category Archives: Advanced EM

Advanced Electromagentism (Phys 341)

Project Plan: Van Allen Belts

Summary:

The primary goal of my project is to create a 3d model of the shape and strength of the Earth’s magnetic field and define the locations of the Van Allen Belts within that model. According to the research I have done so far, a planetary magnetic field resembles the field of cylinder. Applying relevant Earth properties, I would then be able to create an initial model of the field.  Furthermore, due to the proximity of these belts to the Earth, I will not have to take interactions with the solar wind into account when modeling the field. The modeling will be done with the Mathematica program. With the model complete, I would hope to compare it to other, more exact models of the Earth’s magnetic field to confirm the theoretical location of the Van Allen Belts. I would also be interested in noting if there is any relationship between core size of the planet and development of a magnetic field. My current research hasn’t turned up any leads for a mathematical way to approach this problem however.

Timeline:

•Week  1: (week of 4/6) Research the Van Allen Belts and Define Project Parameters -During this first week I plan to research the different possible facets of my project in order to determine the particular parameters I will be creating the 3d model with. This also includes looking for previously made 3d vector fields that can teach me how to plot the vector field in Mathematica. Furthermore I will be looking into some of the secondary objectives of my project to see if the ideas can be executed in a reasonable amount of time.

•Week 2: (week of 4/13) Creating the Initial 3D Model – During the second week of the project, we proceed onto the next step of creating our basic 3D magnetic field model. This 3D vector field model will be created using Mathematica and will create a visual representation of the Earth’s magnetic field. The initial model will be based off of the magnetic field of a cylinder, a design which has been suggested by multiple sources.

•Week 3: (week of 4/20) Finishing the Initial 3D Model and Model Comparisons – This week will be used to put any necessary finishing touches on the initial model and determine the location of the Van Allen belts within the model. I will also be comparing the model to observed data and other proposed models of the field. From these findings, I will be able to determine the accuracy of the field modeled in Mathematica. If the simple cylindrical model is not as accurate as predicted, this week will also be taken to edit the model and improve its accuracy.

•Week 4: (week of 4/27) Extended Modeling – During this week I will finish all alterations on a final edited model. If there is extra time, the current plan is to systematically alter the model to see how certain changes effect the magnetic field. Specifically my goal is to see if there exists some sort of correlation between the planet’s core size and the development of its magnetic field and subsequently its Van Allen Belts. If a correlation like this can be seen, the magnetic fields of other planets will be modeled and compared to actual data. This will allow us to confirm if the created model can be applied to other planets with only minor alterations to its coding.

•Week 5: (week of 5/4) Finishing Touches – During this week, any extra modeling will be quickly finished up and the rest of the week will be dedicated to organizing the collected data into a final presentation.

Sources:

Currently the sources I have browsed are:

http://www.phy6.org/Education/Iradbelt.html

http://vanallenprobes.jhuapl.edu/science/overview.php

https://www.spenvis.oma.be/help/background/traprad/traprad.html#APAE

http://www.nasa.gov/mission_pages/rbsp/main/index.html#.U0O-7fmIDlx

Share

Project Plan: Modeling Mie Scattering in the Interstellar Medium (ISM) (adjusted)

Resources

  1. Introduction to Electrodynamics, 4th ed. by David J. Griffiths
  2. Physics of the Galaxy and Interstellar Matter by H. Scheffler and H. Elsässer
  3. Interstellar Grains by N.C. Wickramasinghe
  4. Physical Processes in the Interstellar Medium by Lyman Spitzer, Jr.
  5. The scattering of light, and other electromagnetic radiation by Milton Kerker
  6. Mathematica 9 Help Documentation Center (the most valuable resource!)

Project Description

I will be exploring Mie theory and modeling this type of scattering for particles present in the interstellar medium (ISM). There are a number of parameters that can be easily derived from applying Mie theory to the ISM, including an asymmetry parameter (g), extinction coefficients, albedo, and phase functions. I will focus first on modeling the asymmetry parameter (g), but time permitting, will continue onto other properties as I move into Week 3 – as stated in my timeline (below).

While the space between stars and galaxies appears quite vast and barren given only the access of our eyes fixed quaintly at ground level, the ISM is teeming with a variety of matter and electromagnetic waves. These regions are rich with gas (atomic and molecular), dust, and are permeated by electromagnetic waves, or radiation, from starlight (and occasionally other sources). Observations of various astrophysical phenomena show that along a given line of sight, their is “extinction” of this radiation. Scattering and absorption account for these observations and occur due to the presence of various dust grains within the ISM. This is where Mie scattering fits into modeling the asymmetry parameter (g), a measure of the fraction of light scattered in the forward direction. Our efforts towards modeling this relationship as well as the values of other dust grain properties such as size, composition, etc, begins with a preliminary comprehension of Mie’s work.

In 1908, Mie was working well before the substantially assistive mechanisms of modern computational modeling. Although his successors refined the theory of scattering (for spherical particles) over subsequent years, Mie’s initial work is fitting for the relatively fundamental level of analysis in this course. As Kerker explains (5), the basic scattering functions can be derived from a process whereby the proper Ricati-Bessel function is chosen and scattering coefficients are derived:

a_n=\frac{\psi_n(\alpha)\psi'_n(\beta)-m\psi_n(\beta)\psi'_n(\alpha)}{\zeta_n(\alpha)\psi'_n(\beta)-m\psi_n(\beta)\zeta'_n(\alpha)}

and

b_n=\frac{m\psi_n(\alpha)\psi'_n(\beta)-\psi_n(\beta)\psi'_n(\alpha)}{m\zeta_n(\alpha)\psi'_n(\beta)-m\psi_n(\beta)\zeta'_n(\alpha)}

where m indicates an index of refraction, \psi_n and \zeta_n (and their respective primes) are the Ricati-Bessel functions chosen, and \alpha and \beta are constants given by wave parameters (k, etc). These scattering coefficients are then combined with a mathematical tool called a “Legendre polynomial” to give amplitude functions for the scattering. Other parameters can then be derived once these functions are modeled.

Tools

  1. Mathematica
  2. LaTeX

Timeline

Week 1 (4/7 – 4/13)

I will refresh and further extend my knowledge of Mathematica and continue my research into the computational and theoretical aspects of Mie scattering in the context of the interstellar medium (ISM). As my project is computationally based, I will focus heavily on bridging the divide between my theoretical knowledge of scattering in the ISM and my work in Mathematica.

Week 2 (4/14 – 4/20)

For Week 2 I plan on completing a working Mathematica model for the asymmetry parameter, g, and complimenting this work as needed with research into Bessel and Ricati-Bessel functions. Mie theory is founded in the rigors of these functions and gives solutions to Maxwell’s equations that illustrates the scattering of waves by spherical particles. Specifically useful with the Bessel and Ricati-Bessel functions are the eponymous differential equations. If this work is completed I will move on to Week 3 work.

Week 3 (4/21 – 4/27)

I will continue modeling. My initial research into the theory will be added to as needed. As time permits, I will continue on to explore the utility of Mie theory and scattering within the ISM as it relates to the derivation of other interstellar grain properties.

Week 4 (4/28 -5/4)

I will finalize any lingering modeling. My results will be nearly all in and I will begin to wrap up my blog – focusing on visualizations (plots and animations) and ensuring that they function properly within the blog space. This week will be mainly devoted to polishing off my blog posts (data and results especially), i.e. making all aspects of the blog look aesthetically pleasing.

Week 5 (5/5 – 5/11)

This week concludes my project as I finish commenting on my peer’s blog posts.

Collaborators

While I plan on working alone, Professor Magnes will be assisting and advising as this project progresses. Both of my predecessors focused on the theory and modeling of Rayleigh scattering – a related phenomena but still outside of the purview of my project. I intend to move in a direction much different than my predecessors who explored scattering of the Rayleigh domain. I do, however, anticipate that as my project develops, I will be reflecting on my results and the possibility exists to compare and contrast them in the context of the work done by these individuals. I cannot predict what these comparisons may entail, but as I conclude my project, these ties may reflect elements shared between background theory, computational processes, and my results.

Share

Project Plan: Capacitors

Goal:
Some features of real capacitors are sometimes ignored for pedagogical purposes, notably fringing fields. I intend to model a capacitor and its features, such as energy storage and capacitance, while making as few assumptions as possible, for example by paying attention to fringing effects (though assumptions, approximations, and numerical techniques will still be used as needed).

Methods and Comments:
Mathematica 9 will be used as the only computational tool to model a 3-dimensional capacitor. First, I intend to model the electric field of a rectangular conducting plate with uniform surface density σ. Then, using the principle of electric field superposition, I will find the combined field of this plate and that of an oppositely charged, geometrically identical plate offset by a small distance normal to the plane (i.e. a parallel plate capacitor). These fields will be based on Coulomb’s Law for a surface charge density:

In addition, 3 approximations will be used: the simple capacitor field approximation  to be quickly sure that the above results are correct, an electric field built using Mathematica’s NIntegrate function, which may be needed if the default Integrate fails to evaluate efficiently, and an approximation of my own design I call the “grid model,” whereby a charged sheet is replaced by a fine grid of hundreds or thousands of appropriately charged point charges. This may be necessary for oddly-shaped capacitors, and if it is sufficiently accurate, to “fill in the gaps” where other methods take too long and/or are inaccurate. Mathematica’s Timing function will be particularly useful for determining the efficiency of methods.
After the electric field computations have been done, the effects of a dielectric sandwiched between the plates can be analyzed using the principles of Griffiths, chapter 4. For example, once the electric field at a set of points in the capacitor has been found, one can, assuming linear dielectrics, apply  to find the electric displacement, and hence the energy stored in the configuration from the equation . This can be compared to stated values by capacitor manufacturers.

Preliminary Results:
My exact-value method based on Coulomb’s law works for a charged rectangular sheet in the xy-plane. At a point directly above the plate’s center at a distance reasonable for a capacitor (1% the width), the integral takes 9 seconds to evaluate; not unreasonable if time and ambition are budgeted. However, at a point half-way between the center and a corner, the program evaluated after 10 minutes, demonstrating the complexity of a seemingly simple integral. Using the grid method for a configuration of 40,000 point charges, however, yielded results that were 99.998% accurate in less than three seconds; the accuracy was barely lower for a 10,000 charge grid, which took half a second to evaluate. The grid method was also much more accurate than the infinite plane approximation taught in introductory physics, accounting for the finite dimensions of the sheet.

Time Line:
– Week 1: Further refine, test, and expand my existing models to work for more arbitrarily shaped plates.
– Week 2: Model the properties of simple parallel plate capacitors of rectangular and circular shapes.
– Week 3: Model the properties of more complicated capacitors, for example rolled up capacitors or variable capacitors.
– Week 4: Possibly account for more complicated properties of dielectrics, such as non-linearity. If this proves unmanageable, I may simply extend the work of week three.
– Week 5: Compare more thoroughly my models to real capacitors based on information from manufacturers and/or other sources. Also, this week, for which no computational work is budgeted, can be used as a safety net if previous weeks do not run as smoothly as I anticipate.

Collaborator(s): N/A

Resources:
– Griffiths “Introduction to Electrodynamics”, 4th Edition (this will be the primary source of information and equations that will be translated to Mathematica)

– Mathematica 9, Student Edition, including its extensive documentation.

– A relatively new edition of the “CRC Handbook of Chemistry and Physics” for values of the permittivities of different dielectric materials. Not yet procured.

– I am considering a resource on real capacitors, their energy storing capabilities, dimensions, and dielectric media to compare my values to the real objects I am modeling. However, at this early point in the project, this has not yet been procured nor will it likely be needed until week 3. Further, Griffiths has permittivity data, which may be sufficient.

– Through V-Apps, I may need to access more powerful computers than my 2011 laptop for intense computational work.

Share

Project Plan: A Guide To Convolution In Action

Description of project

Convolution is the theory behind interpreting the data presented. When physicists use optical tools for their experiments they need to understand whether the optics they are using will transmit the proper information. In practice one is limited to the material of the filters, as the wave fronts get distorted by the material they pass through. In order to be able to work with what you have, physicists model their possible optics layout before purchasing the optics. To retrieve the desired information physicists model the convoluted wave front, and then prepare a good deconvolution mechanism that in practice should yield the necessary data. This project is an attempt to understand convolution and deconvolution of electromagnetic waves through optical filters. I will be exploring the theory behind convolution, demonstrate examples of convolution, attempt deconvolution of a convoluted distributions, and then hopefully show a real world example of actual optical filters.

Theory

Convolution is the mixture of functions that individually have known Fourier transforms. A Fourier transform is the transformation of a square-integrable function f(x) from one domain to another (5). It is defined as such:

f(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty }^{\infty }\!\Phi(k)e^{ikx}dk \qquad \Phi(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty }^{\infty }\!f(x)e^{-ikx}dx

Both the function and the Fourier transform describe the same system though under different but related spaces (See: Plancherel’s Theorem). The advantage is if you have a machine that measures time but you are trying the measure the system as a function of frequency, then you can measure the system with that machine and simply take the Fourier transform of your data. Unfortunately, the deviations of the Fourier pairs are bounded by the uncertainty principle. A function with a narrow spread will yield a transformation with a wider spread, and vice versa.

\sigma^2_\Psi\sigma^2_\Omega\geq\left(\frac{1}{2i}\langle[\hat{\Psi},\hat{\Omega}]\rangle\right)^2

where \hat{\Psi} and \hat{\Omega} are two arbitrary operators, and \sigma_{i} is the standard deviation.

The definition of a convolution of two functions is defined as follows:

f_{1}(x)\ast f_{2}(x)=\int_{-\infty }^{\infty }\!f_{1}(x')f_{2}(x-x')\mathrm{d}x' \\ \\ \Phi_{1}(k)\ast \Phi_{2}(k)=\int_{-\infty }^{\infty }\!\Phi_{1}(k')\Phi_{2}(k-k')\mathrm{d}k'

The convolution theorem then states that the Fourier transform of a convolution is the product of the Fourier transforms to a factor of \sqrt{2\pi}. Similarly, the Fourier transform of a product of functions is the convolution of the Fourier transforms (5):

{\widehat_{f_{1}\ast f_{2}}} (x)= \sqrt{2\pi}\;{\Phi_1}(k)\cdot {\Phi_2}(k) \qquad {\widehat_{f_{1}\cdot f_{2}}} (x)= \frac{1}{\sqrt{2\pi}}\;{\Phi_1}(k)\ast {\Phi_2}(k)

The implication of this theorem is if any arbitrary curve can be expressed as a product of functions with given Fourier counterparts, then it can undergo deconvolution to yield the desired data as represented by known functions (3).

f_{1}(x)\ast f_{2}(x)\rightleftharpoons \Phi_{1}(k)\cdot \Phi_{2}(k)

Timeline

 All work will either be done on my computer or at the sci-vis lab.

Week 1: I will become familiar with Professor Magnes’s MATLAB script and reconstruct it in Mathematica. I will use the information provided for me in the texts to create new examples of various convoluted distributions. I will also provide an introduction to the theory that pertains to my project.

Week 2: By now I should be familiar enough with Mathematica to display some cool examples. I will attempt to provide an example of real world convolution of two optical filters from thorlabs. In practice convolution of two actual filters is not as easy as adding two equations. I will need to figure out how to generally apply my ideal examples to sets of data.

Week 3: I will now attempt to demonstrate the deconvolution of a distribution. I will show this by using one of my previous examples. In theory I should be able to demonstrate proper deconvolution of two functions.

Week 4: Now that I have demonstrated deconvolution, I should be able to demonstrate deconvolution of the data I had previously showed in convolution form. This would be very tricky but hopefully I should be able to succeed.

Week 5: I may be setting the bar up too high, so possibly some of my work will take more time than expected. I should be finished with everything now. Here I will tweak my project, and conclude my demonstration.

Note: I may stray from my timeline, but that is only because I got caught up in an interesting phenomenon. Should I decide to alter my direction, I will update my timeline accordingly.

Resources

Will be updated if necessary

(1) Griffiths, David J. Introduction to Electrodynamics. Upper Saddle River, NJ: Prentics Hall, 1999. Print.

(2) Hecht, Eugene. Optik. München: Oldenbourg, 2001. Print.

(3) James, J. F. A Student’s Guide to Fourier Transforms: With Applications in Physics and Engineering. Cambridge: Cambridge UP, 2011. Print.

(4) Pedrotti, Frank L., Leno S. Pedrotti, and Leno Matthew. Pedrotti. Introduction to Optics. Upper Saddle River, NJ: Pearson Prentice Hall, 2007. Print.

(5) Sadun, Lorenzo Adlai. Applied Linear Algebra: The Decoupling Principle. Providence, RI: American Mathematical Society, 2008. Print.

Question to the reader: Is the verb of deconvolution: deconvolve or deconvolute?

Share

Project Plan: RLC Circuits

Plan/Goals:

In this project, I plan to study the relevant differential equations that govern RLC circuits and use Mathematica to solve them for values that are useful. The general equation governing a basic RLC circuit with a capacitor, voltage, resistor, and inductor in series, in that order is:

LI'(t)+RI(t)+\frac{1}{C}Q(t)=V(t) [Equation 1] (UBC- Source 4)

which, when going through a series of substitutions, becomes:

LI''(t)+RI'(t)+\frac{1}{C}I(t)=\omega E_{0}cos(\omega t) [Equation 2] (UBC- Source 4)

Equation 1 has six variables: L (inductance), R (resistance), C (capacitance), V (voltage), Q (charge), and I (current). When a circuit like this is set up in the lab, the values that are known are L, R, C, and V because they directly depend on the components of the circuit. Once the differential equation [2] is solved, values for current (I) and charge (Q) can be determined. I will use Mathematica to solve for the general solution to this differential equation [2], which is a second-order differential equation. Once I have the general solution, I will vary the initial conditions to determine the effect of different circuit components on the overall properties of the circuit. Following this, I will develop more series RLC circuits with components that are set up differently in terms of their component structure.

Timeline (Weeks 1-5):

Week 1: I will begin by reviewing basic differential equation solving techniques for first and second order differential equations. I will also study the differential equation solving capabilities of Mathematica and review the techniques for solving second-order differential equations as they apply to RLC circuits.

Week 2: I plan on solving for the general solution to Equation 2 above (using Mathematica). I will vary different initial conditions and create graphs that visualize the changes that occur. I will also have a visual representation of the circuit.

Week 3: Develop another series circuit or study a previously built one. Determine the general equation for it and begin the solution process.

Week 4: Finalize the solution for the second circuit. Develop graphs for visualization purposes.

Week 5: I will finalize my project by proofreading all the components and making sure everything is presentable. I will also provide constructive criticism to my peers on their projects.

Sources:

1. Mathematica Cookbook by Sal Mangano

2. Electronic Circuit Analysis for Scientists by James A. McCray and Thomas A. Cahill

3. Dynamical Systems with Applications using Mathematica by Stephen Lynch

4. The RLC Circuit- University of British Columbia- http://www.math.ubc.ca/~feldman/m121/RLC.pdf

5. Class Notes- Mathematics 228 (Methods of Applied Mathematics) taught by Matthew Miller

Collaborators:

N/A

 

Share

Project Plan: Relativistic E&M

Sources: In terms of sources, this project is fairly simple. The main source will be Chapter 12 of Griffiths’ Introduction to Electrodynamics, 3rd ed. This will provide a framework for deriving the transformation equations.

Process/Timeline: There are five main steps involved in this project:

1) 4/7-4/14: Derive the transformation equations. This will be a proof-based step, and I need to refresh myself on some of the concepts of mechanical relativity, so it may take some time.

2) 4/14-4/18: Pick one or two simple scenarios and find their E- and B- fields if they were traveling in a moving reference frame. This will be a computational step. The transformation equations are pretty straightforward, so it should take less time. This is just to have a proof of concept, so it is less important that the system has interesting behavior in a moving reference frame.

3) 4/18-4/24: Make 3D or 2D vector field models of these situations in Mathematica. This portion will be focused on figuring out how to make mathematica do what I want. The goal is to come up with an animation or interactive figure that can be used to view the vector fields when the system is moving at different speeds.

4) 4/24-5/2: Find and model situations that display either representative or unusual behavior when considered in a relativistic reference frame. Once the Mathematica simulation for the first situation has been figured out, the following cases should be easier to take care of. Interesting behavior might include systems that only have an electric field in one reference frame and only a magnetic frame in another. It also may be interesting to consider what happens if a reference frame is moving faster than the speed of light.

5) 5/15/14: Summarize results and write conclusions. This will consist of a final look at the systems considered earlier and suggest possible directions for future exploration.

Share

Project Plan: Electric & Magnetic Field Modeling

Sources:

  • Introduction to Electrodynamics by David J. Griffiths, Fourth Edition: Chapter 5

Model:

I will be creating models of the magnetic fields of a bar magnet, sphere and a cylinder. Each of these fields will be first be derived for continuous distributions and then modeled on Mathematica using its Vector Field plot function in 2 and 3 dimensions. Time-permitting, I will also model the magnetic fields for distributions that are not continuous (perhaps with varying current densities dependent on space J(r)). Example systems can be found in Griffiths’ Introduction to Electrodynamics exercises.

Timeline:

April 7-April 14: Complete project proposal and begin derivations

April 14-April 21: Alter project proposal as needed and complete derivations

April 21- April 28: Post derivations and begin Mathematica modeling

April 28-May 5: Final Mathematica modeling and combination with Peter’s Modeling

Collaborators:

I will be working with Peter Florio, who will derive and model the electric fields of the same distributions. We plan to compare our results side-by-side to observe the similarities and differences between our models and to notice the parallels in our derivations.

Share

Project Plan: Modeling Electric and Magnetic Fields

What will be modeled:

I will be modeling the electric fields of a bar magnet, cylinder and sphere. The derivations of the field geometries will be shown in a step by step process and then will be modeled with Mathematica. More complex systems taken from examples in Introduction to Electrodynamics may be used an modeled as well, time permitting.

Timeline:

April 7-April 14: Complete project proposal and begin derivations

April 14-April 21: Alter project proposal as needed and completed derivations

April 21- April 28: Post derivations and begin Mathematica modeling

April 28-May 5: Final Mathematica modeling and combination with Cedric’s Modeling

Collaborators:

I will be working with Cedric Chang who will derive and model the magnetic fields of the same objects that I model the electric fields of. At the end, both of our models will be combined to display both electric and magnetic fields of the shapes in question.

Sources:

Introduction to Electrodynamics by David J. Griffiths, Third Edition

Share

Project Proposal: Measuring and Modeling Physical RCL Circuits.

This project is based on an initial interest in the RLC circuit lab in 114 where students put together parts of a radio and demonstrated how inductance and capacitance was used to tune a radio. My end goal is to compare measurements across components of a real RLC circuit (radio) to the ideal values one might expect to find based on equations from our textbook that model these circuits. I would begin with a simple LC circuit, maybe constructed out of components that would later be found in the radio circuit (or whatever components are available to make the simplest LC circuit I can make measurements on). I would collect data such as potential across various components. An important part of the analysis would be proposing possible/probable causes of any discrepancy between expected values and experimental values. I would use an oscilloscope to make the measurements. Ideally I would use a computer oscilloscope and a laptop and set up in room 203A.

Share

Project Plan: Rail Gun

Sources/Resources:

  1. Introduction to Electrodynamics by David J. Griffiths
  2. http://web.mit.edu/mouser/www/railgun/physics.html
  3. http://www.dtic.mil/dtic/tr/fulltext/u2/a345008.pdf
  4. https://physics.le.ac.uk/journals/index.php/pst/article/viewFile/468/275
  5. http://www.instructables.com/id/Rail-Gun-Linear-Accelerator/
  6. Vassar College Lab Technicians

Materials:

  1. LaTeX and Mathematica Software
  2. Pen and Paper for derivations
  3. Gas Reservoirs
  4. Gas Valves
  5. Steel Tube
  6. Pneumatic Pipes
  7. 10 400 Volts 450 uF Capacitors
  8. Solid Aluminum Bar
  9. Acrylic

General Project Plan:

The first and most important part of our project is to use Mathematica to model the magnetic fields, current, capacitance, and eventually forces/equations of motion of a generic rail gun. This will require a great deal of derivation using principles from Griffith’s book, and a working knowledge of Mathematica. We have found several resources online that will help us through the derivation process.

The rail gun will essentially be made of four components: a power supply, two rails, and a sliding bridge with a projectile attached. This bridge will complete the circuit. The current will create a magnetic field and push the projectile/bridge forward. This motion generates a number of interesting properties which we hope to model on Mathematica.

We will build a rail gun using materials both from the lab and that we acquire independently. After doing so, we will take a video of the rail gun using Vassar’s high speed camera. We then will use video analysis software like LoggerPro to analyze our results and compare them to known existing value and the values that we calculate.

Estimated Time Line:

Week 1 (4/6-4/12): Acquire working knowledge of Mathematica and begin hand derivations of relevant equations and concepts. Make list of materials required for assembly of railgun.

Some basic equations we will work with are:

Biot Savart-

(1)   \begin{equation*} B(t)=\frac{I(t)\mu_0}{4\pi}\int\frac{dl \times r}{r^2}\ \end{equation*}

Ampere’s Law-

(2)   \begin{equation*} \nabla \times B = \mu_0J + \mu_0\epsilon_0\frac{\partial E}{\partial t} \end{equation*}

Ohm’s Law-

(3)   \begin{equation*} I(t)R = V(t) - \varepsilon(t) \end{equation*}

Resistance-

(4)   \begin{equation*} R = \frac{\rho l}{A} \end{equation*}

I will apply these equations to our specific case and find how they change with time specific to the parameters.

Week 2 (4/13-4/19): Finish my models of current and resistance as functions of time. Begin to plot them on Mathematica. Attain all materials for assembly of rail gun

Week 3 (4/20-4/26): Finish modeling current, resistance, and capacitance on Mathematica. Combine my results with John’s results to model equations of motion. Finish assembly of rail gun

Week 4 (4/27-5/3): Test rail gun and compare results to our experiment. If time permits, factor different mediums/materials into the Mathematica models.

Collaborator:

I will be working with John Loree. He will use mathematica to model the induced magnetic field and forces upon the railgun. Together, we will build the railgun.

Share