Project Plan: A Guide To Convolution In Action

Description of project

Convolution is the theory behind interpreting the data presented. When physicists use optical tools for their experiments they need to understand whether the optics they are using will transmit the proper information. In practice one is limited to the material of the filters, as the wave fronts get distorted by the material they pass through. In order to be able to work with what you have, physicists model their possible optics layout before purchasing the optics. To retrieve the desired information physicists model the convoluted wave front, and then prepare a good deconvolution mechanism that in practice should yield the necessary data. This project is an attempt to understand convolution and deconvolution of electromagnetic waves through optical filters. I will be exploring the theory behind convolution, demonstrate examples of convolution, attempt deconvolution of a convoluted distributions, and then hopefully show a real world example of actual optical filters.

Theory

Convolution is the mixture of functions that individually have known Fourier transforms. A Fourier transform is the transformation of a square-integrable function f(x) from one domain to another (5). It is defined as such:

f(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty }^{\infty }\!\Phi(k)e^{ikx}dk \qquad \Phi(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty }^{\infty }\!f(x)e^{-ikx}dx

Both the function and the Fourier transform describe the same system though under different but related spaces (See: Plancherel’s Theorem). The advantage is if you have a machine that measures time but you are trying the measure the system as a function of frequency, then you can measure the system with that machine and simply take the Fourier transform of your data. Unfortunately, the deviations of the Fourier pairs are bounded by the uncertainty principle. A function with a narrow spread will yield a transformation with a wider spread, and vice versa.

\sigma^2_\Psi\sigma^2_\Omega\geq\left(\frac{1}{2i}\langle[\hat{\Psi},\hat{\Omega}]\rangle\right)^2

where \hat{\Psi} and \hat{\Omega} are two arbitrary operators, and \sigma_{i} is the standard deviation.

The definition of a convolution of two functions is defined as follows:

f_{1}(x)\ast f_{2}(x)=\int_{-\infty }^{\infty }\!f_{1}(x')f_{2}(x-x')\mathrm{d}x' \\ \\ \Phi_{1}(k)\ast \Phi_{2}(k)=\int_{-\infty }^{\infty }\!\Phi_{1}(k')\Phi_{2}(k-k')\mathrm{d}k'

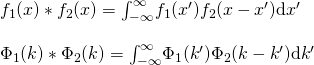
The convolution theorem then states that the Fourier transform of a convolution is the product of the Fourier transforms to a factor of \sqrt{2\pi}. Similarly, the Fourier transform of a product of functions is the convolution of the Fourier transforms (5):

{\widehat_{f_{1}\ast f_{2}}} (x)= \sqrt{2\pi}\;{\Phi_1}(k)\cdot {\Phi_2}(k) \qquad {\widehat_{f_{1}\cdot f_{2}}} (x)= \frac{1}{\sqrt{2\pi}}\;{\Phi_1}(k)\ast {\Phi_2}(k)

The implication of this theorem is if any arbitrary curve can be expressed as a product of functions with given Fourier counterparts, then it can undergo deconvolution to yield the desired data as represented by known functions (3).

f_{1}(x)\ast f_{2}(x)\rightleftharpoons \Phi_{1}(k)\cdot \Phi_{2}(k)

Timeline

 All work will either be done on my computer or at the sci-vis lab.

Week 1: I will become familiar with Professor Magnes’s MATLAB script and reconstruct it in Mathematica. I will use the information provided for me in the texts to create new examples of various convoluted distributions. I will also provide an introduction to the theory that pertains to my project.

Week 2: By now I should be familiar enough with Mathematica to display some cool examples. I will attempt to provide an example of real world convolution of two optical filters from thorlabs. In practice convolution of two actual filters is not as easy as adding two equations. I will need to figure out how to generally apply my ideal examples to sets of data.

Week 3: I will now attempt to demonstrate the deconvolution of a distribution. I will show this by using one of my previous examples. In theory I should be able to demonstrate proper deconvolution of two functions.

Week 4: Now that I have demonstrated deconvolution, I should be able to demonstrate deconvolution of the data I had previously showed in convolution form. This would be very tricky but hopefully I should be able to succeed.

Week 5: I may be setting the bar up too high, so possibly some of my work will take more time than expected. I should be finished with everything now. Here I will tweak my project, and conclude my demonstration.

Note: I may stray from my timeline, but that is only because I got caught up in an interesting phenomenon. Should I decide to alter my direction, I will update my timeline accordingly.

Resources

Will be updated if necessary

(1) Griffiths, David J. Introduction to Electrodynamics. Upper Saddle River, NJ: Prentics Hall, 1999. Print.

(2) Hecht, Eugene. Optik. München: Oldenbourg, 2001. Print.

(3) James, J. F. A Student’s Guide to Fourier Transforms: With Applications in Physics and Engineering. Cambridge: Cambridge UP, 2011. Print.

(4) Pedrotti, Frank L., Leno S. Pedrotti, and Leno Matthew. Pedrotti. Introduction to Optics. Upper Saddle River, NJ: Pearson Prentice Hall, 2007. Print.

(5) Sadun, Lorenzo Adlai. Applied Linear Algebra: The Decoupling Principle. Providence, RI: American Mathematical Society, 2008. Print.

Question to the reader: Is the verb of deconvolution: deconvolve or deconvolute?

Project Plan: RLC Circuits

Plan/Goals:

In this project, I plan to study the relevant differential equations that govern RLC circuits and use Mathematica to solve them for values that are useful. The general equation governing a basic RLC circuit with a capacitor, voltage, resistor, and inductor in series, in that order is:

LI'(t)+RI(t)+\frac{1}{C}Q(t)=V(t) [Equation 1] (UBC- Source 4)

which, when going through a series of substitutions, becomes:

LI''(t)+RI'(t)+\frac{1}{C}I(t)=\omega E_{0}cos(\omega t) [Equation 2] (UBC- Source 4)

Equation 1 has six variables: L (inductance), R (resistance), C (capacitance), V (voltage), Q (charge), and I (current). When a circuit like this is set up in the lab, the values that are known are L, R, C, and V because they directly depend on the components of the circuit. Once the differential equation [2] is solved, values for current (I) and charge (Q) can be determined. I will use Mathematica to solve for the general solution to this differential equation [2], which is a second-order differential equation. Once I have the general solution, I will vary the initial conditions to determine the effect of different circuit components on the overall properties of the circuit. Following this, I will develop more series RLC circuits with components that are set up differently in terms of their component structure.

Timeline (Weeks 1-5):

Week 1: I will begin by reviewing basic differential equation solving techniques for first and second order differential equations. I will also study the differential equation solving capabilities of Mathematica and review the techniques for solving second-order differential equations as they apply to RLC circuits.

Week 2: I plan on solving for the general solution to Equation 2 above (using Mathematica). I will vary different initial conditions and create graphs that visualize the changes that occur. I will also have a visual representation of the circuit.

Week 3: Develop another series circuit or study a previously built one. Determine the general equation for it and begin the solution process.

Week 4: Finalize the solution for the second circuit. Develop graphs for visualization purposes.

Week 5: I will finalize my project by proofreading all the components and making sure everything is presentable. I will also provide constructive criticism to my peers on their projects.

Sources:

1. Mathematica Cookbook by Sal Mangano

2. Electronic Circuit Analysis for Scientists by James A. McCray and Thomas A. Cahill

3. Dynamical Systems with Applications using Mathematica by Stephen Lynch

4. The RLC Circuit- University of British Columbia- http://www.math.ubc.ca/~feldman/m121/RLC.pdf

5. Class Notes- Mathematics 228 (Methods of Applied Mathematics) taught by Matthew Miller

Collaborators:

N/A

 

Project Plan: Relativistic E&M

Sources: In terms of sources, this project is fairly simple. The main source will be Chapter 12 of Griffiths’ Introduction to Electrodynamics, 3rd ed. This will provide a framework for deriving the transformation equations.

Process/Timeline: There are five main steps involved in this project:

1) 4/7-4/14: Derive the transformation equations. This will be a proof-based step, and I need to refresh myself on some of the concepts of mechanical relativity, so it may take some time.

2) 4/14-4/18: Pick one or two simple scenarios and find their E- and B- fields if they were traveling in a moving reference frame. This will be a computational step. The transformation equations are pretty straightforward, so it should take less time. This is just to have a proof of concept, so it is less important that the system has interesting behavior in a moving reference frame.

3) 4/18-4/24: Make 3D or 2D vector field models of these situations in Mathematica. This portion will be focused on figuring out how to make mathematica do what I want. The goal is to come up with an animation or interactive figure that can be used to view the vector fields when the system is moving at different speeds.

4) 4/24-5/2: Find and model situations that display either representative or unusual behavior when considered in a relativistic reference frame. Once the Mathematica simulation for the first situation has been figured out, the following cases should be easier to take care of. Interesting behavior might include systems that only have an electric field in one reference frame and only a magnetic frame in another. It also may be interesting to consider what happens if a reference frame is moving faster than the speed of light.

5) 5/15/14: Summarize results and write conclusions. This will consist of a final look at the systems considered earlier and suggest possible directions for future exploration.

Project Plan: Electric & Magnetic Field Modeling

Sources:

  • Introduction to Electrodynamics by David J. Griffiths, Fourth Edition: Chapter 5

Model:

I will be creating models of the magnetic fields of a bar magnet, sphere and a cylinder. Each of these fields will be first be derived for continuous distributions and then modeled on Mathematica using its Vector Field plot function in 2 and 3 dimensions. Time-permitting, I will also model the magnetic fields for distributions that are not continuous (perhaps with varying current densities dependent on space J(r)). Example systems can be found in Griffiths’ Introduction to Electrodynamics exercises.

Timeline:

April 7-April 14: Complete project proposal and begin derivations

April 14-April 21: Alter project proposal as needed and complete derivations

April 21- April 28: Post derivations and begin Mathematica modeling

April 28-May 5: Final Mathematica modeling and combination with Peter’s Modeling

Collaborators:

I will be working with Peter Florio, who will derive and model the electric fields of the same distributions. We plan to compare our results side-by-side to observe the similarities and differences between our models and to notice the parallels in our derivations.

Project Plan: Modeling Electric and Magnetic Fields

What will be modeled:

I will be modeling the electric fields of a bar magnet, cylinder and sphere. The derivations of the field geometries will be shown in a step by step process and then will be modeled with Mathematica. More complex systems taken from examples in Introduction to Electrodynamics may be used an modeled as well, time permitting.

Timeline:

April 7-April 14: Complete project proposal and begin derivations

April 14-April 21: Alter project proposal as needed and completed derivations

April 21- April 28: Post derivations and begin Mathematica modeling

April 28-May 5: Final Mathematica modeling and combination with Cedric’s Modeling

Collaborators:

I will be working with Cedric Chang who will derive and model the magnetic fields of the same objects that I model the electric fields of. At the end, both of our models will be combined to display both electric and magnetic fields of the shapes in question.

Sources:

Introduction to Electrodynamics by David J. Griffiths, Third Edition

Project Proposal: Measuring and Modeling Physical RCL Circuits.

This project is based on an initial interest in the RLC circuit lab in 114 where students put together parts of a radio and demonstrated how inductance and capacitance was used to tune a radio. My end goal is to compare measurements across components of a real RLC circuit (radio) to the ideal values one might expect to find based on equations from our textbook that model these circuits. I would begin with a simple LC circuit, maybe constructed out of components that would later be found in the radio circuit (or whatever components are available to make the simplest LC circuit I can make measurements on). I would collect data such as potential across various components. An important part of the analysis would be proposing possible/probable causes of any discrepancy between expected values and experimental values. I would use an oscilloscope to make the measurements. Ideally I would use a computer oscilloscope and a laptop and set up in room 203A.

Project Plan: Rail Gun

Sources/Resources:

  1. Introduction to Electrodynamics by David J. Griffiths
  2. http://web.mit.edu/mouser/www/railgun/physics.html
  3. http://www.dtic.mil/dtic/tr/fulltext/u2/a345008.pdf
  4. https://physics.le.ac.uk/journals/index.php/pst/article/viewFile/468/275
  5. http://www.instructables.com/id/Rail-Gun-Linear-Accelerator/
  6. Vassar College Lab Technicians

Materials:

  1. LaTeX and Mathematica Software
  2. Pen and Paper for derivations
  3. Gas Reservoirs
  4. Gas Valves
  5. Steel Tube
  6. Pneumatic Pipes
  7. 10 400 Volts 450 uF Capacitors
  8. Solid Aluminum Bar
  9. Acrylic

General Project Plan:

The first and most important part of our project is to use Mathematica to model the magnetic fields, current, capacitance, and eventually forces/equations of motion of a generic rail gun. This will require a great deal of derivation using principles from Griffith’s book, and a working knowledge of Mathematica. We have found several resources online that will help us through the derivation process.

The rail gun will essentially be made of four components: a power supply, two rails, and a sliding bridge with a projectile attached. This bridge will complete the circuit. The current will create a magnetic field and push the projectile/bridge forward. This motion generates a number of interesting properties which we hope to model on Mathematica.

We will build a rail gun using materials both from the lab and that we acquire independently. After doing so, we will take a video of the rail gun using Vassar’s high speed camera. We then will use video analysis software like LoggerPro to analyze our results and compare them to known existing value and the values that we calculate.

Estimated Time Line:

Week 1 (4/6-4/12): Acquire working knowledge of Mathematica and begin hand derivations of relevant equations and concepts. Make list of materials required for assembly of railgun.

Some basic equations we will work with are:

Biot Savart-

(1)   \begin{equation*} B(t)=\frac{I(t)\mu_0}{4\pi}\int\frac{dl \times r}{r^2}\ \end{equation*}

Ampere’s Law-

(2)   \begin{equation*} \nabla \times B = \mu_0J + \mu_0\epsilon_0\frac{\partial E}{\partial t} \end{equation*}

Ohm’s Law-

(3)   \begin{equation*} I(t)R = V(t) - \varepsilon(t) \end{equation*}

Resistance-

(4)   \begin{equation*} R = \frac{\rho l}{A} \end{equation*}

I will apply these equations to our specific case and find how they change with time specific to the parameters.

Week 2 (4/13-4/19): Finish my models of current and resistance as functions of time. Begin to plot them on Mathematica. Attain all materials for assembly of rail gun

Week 3 (4/20-4/26): Finish modeling current, resistance, and capacitance on Mathematica. Combine my results with John’s results to model equations of motion. Finish assembly of rail gun

Week 4 (4/27-5/3): Test rail gun and compare results to our experiment. If time permits, factor different mediums/materials into the Mathematica models.

Collaborator:

I will be working with John Loree. He will use mathematica to model the induced magnetic field and forces upon the railgun. Together, we will build the railgun.

Project Plan: Modeling Electromagnetic Fields for Spherical Objects

Sources

I will be utilizing Introduction to Electrodynamics, 4th Edition, by David J. Griffiths. Specifically, I will begin with Gauss’s Law, as defined by Griffiths on page 69:

$ \oint \! \textbf{E} \cdot \mathrm{d} \textbf{a} = \frac{1}{\epsilon_0} Q_{enc} $

Further, I will utilize the formula for the electric field of a point charge below (found on Griffiths page 72), which can be generalized for a spherical object:

$\textbf{E} = \frac{1}{4 \pi \epsilon_0} \frac{q}{r^2} \mathbf{\hat{r}} $

I will additionally work with the magnetic field for the spherical object. Griffiths (page 263) gives the average magnetic field due to uniform current over a sphere as:

$ \textbf{B}_{ave} = \frac{\mu_0}{4 \pi} \frac{\textbf{m}}{R^3}$

Where m is the total dipole moment of the sphere and R is the radius of the sphere.

I will be using Mathematica 9 as my modeling tool.

Plan of Action

I will begin by using the equations above to start with modeling the electric field of a point charge. From there, I will model the electric field for a hollow spherical object. I will create a manipulatable object in Mathematica for changes in radius and charge. I will then move on to modeling the average magnetic field for a spherical object, and attempt to create a manipulatable object akin to the one for electric fields. Next, I will model the electric and magnetic fields for concentric spherical objects, with the goal of ultimately coming up with a very liberal approximation for modeling the magnetic field of the Earth, if the Earth is thought of as several concentric spheres (due to the crust, mantle, and outer/inner cores). However, this will only occur if time permits, as will a preliminary examination of dielectrics.

Timeline

Week 1 (4/6-4/12): Work on the simplest case of a point charge, and learn to work within Mathematica

Week 2 (4/13-4/19): Work to create manipulatable object for electric field of sphere, and begin working on modeling the average magnetic field for a spherical object with uniform current density

Week 3 (4/20-4/26): Model electric and magnetic fields of concentric spherical objects, submit preliminary results on Tuesday on blog

Week 4 (4/27-5/3): Wrap up, submit final data and conclusion on Wednesday, dielectrics if time permits

Collaborators

I am working with Brian Deer, who is focusing on bar magnets, and Tewa Kpulun, who is focusing on cylindrical objects. We will be meeting weekly to discuss our progress, share Mathematica-related insights, and help each other in whatever ways we can.

 

 

John Loree Project Plan: 4/7

Sources and Resources:

1: Introduction to Electrodynamics by David J. Griffiths

2: http://web.mit.edu/mouser/www/railgun/physics.html

3: https://www.carroll.edu/library/thesisArchive/HarmonSFinal_2011.pdf

4: http://physics.wooster.edu/JrIS/Files/Rhoades_Web_Article.PDF

5: http://www.instructables.com/id/Rail-Gun-Linear-Accelerator/

6: Vassar College Laboratory technicians and resources as referred to by Professor Magnes

note: sources and citations may change as data is accrued and decided if needed

Models and Experiments:

The generated magnetic field in the railgun will be modeled using the biot-savart law, ampere’s law, and Faraday’s law. Upon creating and modeling the changing magnetic fields as a function of time, loop size and current, the force upon a slug will then be modeled using the Lorentz force law. As a result of these calculations, we can approximate the theoretical velocity at the end of the rail.

We then intend to build a functional  small scale railgun and test fire it. When testing, we will calculate the velocity upon leaving the rails, and the loss in energy of the projectile over its flight relative to the theoretical values calculated using the models from earlier in the project. Upon the calculation of relative efficiency and accuracy of theoretical models, we will compare our data & values to other railguns that have been produced.

Timeline:

April 16th: complete modeling of the magnetic field as a function of time using mathematica.

April 16th-23rd: construct small scale railgun for test fire with Elias Kim

April 20th: Model the force and velocities of the slug using mathematica.

April 21st: provide the theoretical velocity & range of our small scale railgun

April 22nd: post preliminary data on site using either LaTEX or Mathematica

April 27th: compare theoretical values of railgun to experimental values, upon calculation of relative efficiency of the two reactions, compare our model other railguns constructed.

April 30th and May 1st: prepare presentation and submit final blog

Collaborators:

I will be collaborating with Elias Kim in this project. While I am modeling the magnetic field, induction and force in the railgun, Elias will model the circuitry and current in the railgun. We will then collaborate to generate equations of motion, build the small scale gun and calculate its efficiency. We will regularly collaborate and discuss our projects. However as the project progresses, our roles may shift to split the work evenly between the two of us.

Project Plan: Modeling E and B Fields of a Toroidal Conductor to Explore Tokamak Plasmas

Goal: 

Model the electric and magnetic fields (and D and H) of a solid toroidal conductor with a current flowing through it.  Originally, I intended to model the current as a volume current and vary the aspect ratio of the torus and determine the effects on the fields, but my preliminary research has shown that it is more accurate to model the current as several helically wrapped linear currents, similar to a toroidal solenoid.  I will vary the number of turns (N) and observe the effects of this change.  I will make my decision of initial values based on the values of current tokamak safety factors (safety factor, q{r), describes the ratio of the number of times a given magnetic field line wraps around the torus in the toroidal direction to the number of times it wraps around the torus in the poloidal direction).  Ideally, I will eventually model the tokamak as a series of concentric tori, since these linear helical currents exist throughout the volume of the plasma.  Initially, I will model it as one current along the outside of the plasma, surrounding a conductor

Tentative Methods:

  • Determine the safety factor of, as well typical current through, a tokamak reactor, such as JET (the Joint European Torus).
  • Using the above values, use Maxwell’s Equations to derive expressions for E and B of a torus (expanding upon Griffiths 3rd Ed. Example 5.10); expand this to account for D and H since the interior plasma can be magnetized.
  • Consider how these quantities change as the safety factor of the torus is changed
  • Use Mathematica to model these fields as N changes.

Resources:

  • Griffiths Introduction to Electrodynamics, 3rd Edition
  • Journal article (to be determined – for  JET specifications)

General Notes:

I think that the most difficult part of this will be in creating the model in Mathematica, and getting it to do what I want.  I feel relatively confident about the ease of determining the values to use, and about deriving expression for E and B, though those are not trivial calculations.  Once I have the expressions, it will be relatively simple to vary q(r).

 Schedule:

7 April – 13 April: Research tokamak properties and determine current and size values.  Begin work to derive expressions for B.  Update Project Plan to account for comments.

14 April – 20 April (Tuesday 15 April: Updated Project Plan): Check expressions for B, and then find other fields.  Begin work on building Mathematica model.

21 April – 27 April  (Tuesday  22 April: Preliminary Results): Work on fixing issues with the Mathematica model, and make sure that it works and looks as desired.  Draft conclusion/interpretation of results.  For results, have expressions for all necessary quantities and have a first draft of model.

28 April – 4 May (Thursday 1 May: Begin Presentations): Refine model, and fix any remaining issues.  Elaborate on interpretation of results.  Begin reviewing classmate’s project.