Category Archives: Spring 2014

Preliminary Results- RLC Circuits

Overview

In the following blog post, I discuss my progress with my project so far. I start out with a simple RLC circuit, go on to discuss the components, and derive a solution (using Mathematica) for a circuit with parameters that I have come up with. I then plot current as a function of time and discuss long-term structure in the output of the circuit, its relevance to my project, and my forward plan.

Progress

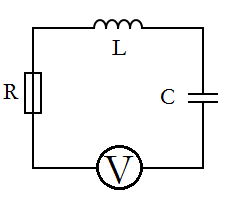
In my plan I discussed a simple RLC circuit that consists of a capacitor, voltage source, resistor, and an inductor. To easily visualize this, I have constructed a basic circuit diagram (Figure 1).

(Figure 1)

The differential equation that governs this RLC circuit is given by

$LI''(t)+RI'(t)+\frac{1}{C}I(t)= E_{0} \omega cos(\omega t)$ [1]

where L is the inductance, R is the resistance, C is the capacitance, I is the current, $\omega$ is the resonant angular frequency, $E_{0}$ is an initial value dependent on the voltage source, and t is the time. The inductance (L), resistance (R), and capacitance (C)are all determined by their respective circuit components, which are easily changed out for different ones. $\omega$ depends on the inductance and capacitance, and its value is given by

$\omega =\frac{1}{\sqrt{LC}}$ [2]

What we have left in terms of variables are current (I) and time (t). For our purposes, time is the independent variable, which leaves the current in the circuit at any time to be the dependent variable. Now that we have established this, we can solve our differential equation [1] for current as a function of time ( $I(t)$ ).

In order to solve [1], I will use the equation solving powers of Mathematica. In particular, the DSolve function is used. When plugged into Mathematica, the input line looks like:

$\text{DSolve}\left[\frac{\text{Current}(t)}{\text{Capacitance}}+\text{Inductance} \text{Current}''(t)+\text{Resistance} \text{Current}'(t)=E_{0} \omega \cos (\omega t),\text{Current}(t),t\right]$ [3]

We must set values for resistance, inductance, capacitance, and $E_{0}$ . For this run through of the solution I chose the following arbitrary values:

Inductance= 1 Henry
Resistance= 10 ohms
Capacitance= .1 farads
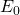$E_{0}$ = 1 Volt

When the command is run with the above values set, Mathematica generates the general solution, which is:

$I(t)=c_1 e^{-8.87298 t}+c_2 e^{-1.12702 t}+0.040824(-Cos(3.162t)+e^{6.661*10^-16t}Cos(3.162t)-0.3564Sin(3.162t)+2.806e^{6.661*10^-16t}Sin(3.162t))$ [4]

First, lets make sure that this solution is reasonable. The known form of the solution to the equation for such a circuit is given by:

$I(t)=c_1 e^{r_{1}t}+c_2 e^{r_{2}t}+Asin(\omega t-\varphi )$ [5]

The form of our equation [4] seems to match up pretty nicely with this known solution [5]. Now, lets examine [4] in more detail.

Our solution [4] looks a little daunting, but we can break it down into its components. The first two terms have constants that depend on the initial current running through the system, i.e. when $I(t)=I(0)$ . However, we can approximate the equation by only looking at the last term, which is a superposition of sin and cosine functions along with a couple exponential terms thrown in. The reason that we can apply this approximation is that the first two terms “damp out” quickly, and thus have exponentially less of an effect as time progresses. The reader may still be curious to see how much of an effect these terms have on the current flowing through the system: to that I say don’t worry! After my initial approximation, I will solve for these constants and compare the two cases.

For now, we will deal with the approximate solution, which is:

$I(t)=0.040824(-Cos(3.162t)+e^{6.661*10^-16t}Cos(3.162t)-0.3564Sin(3.162t)+2.806e^{6.661*10^-16t}Sin(3.162t))$ [6]

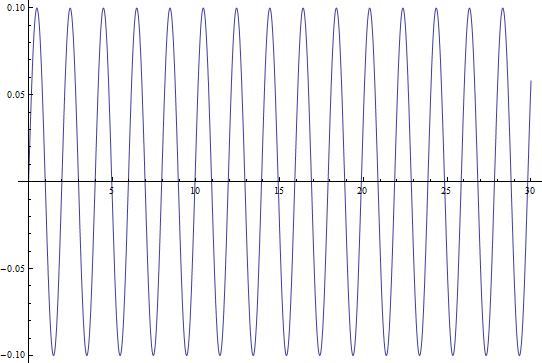
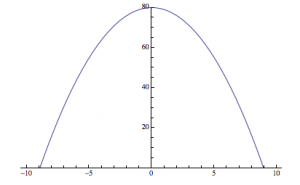
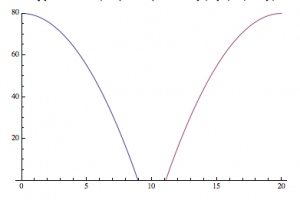
Now that we have this equation, we can use Mathematica to give us an idea of what the changing current looks like over a longer period of time. Figure 2 shows the current in the circuit as a function of time ( $I(t)$ ) plotted over a 30-second interval.

(Figure 2)

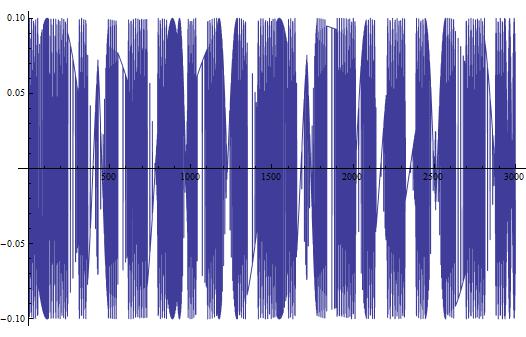
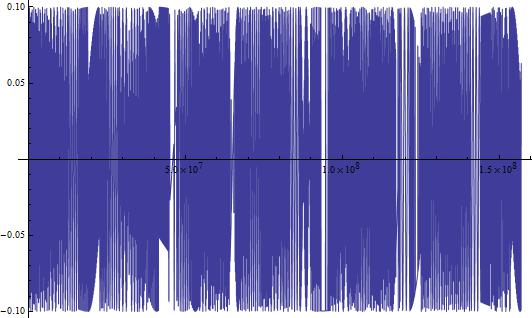
This looks like something we would expect! A sinusoidal wave that describes the changing current over time, just like our equations dictate. But, this is a short time-scale. What happens when we look at the changing current over a longer period of time? In Figure 3, I show the changing current over a longer time period (3000 seconds/50 minutes). In Figure 4, I repeat the process, but with the timescale being 5 years.

(Figure 3)

(Figure 4)

In both Figures 3 and 4, we see some very interesting long-term variations in the current. Why does this occur? Well to be honest, I am not completely certain. I do have a few ideas though:

My first inclination is that the long-term variations are in part due to the approximation I made by removing the first two terms of Equation [4].
My second idea is that these long-term structures are present due to a possible approximation Mathematica may have made when solving the differential equation.
My third and last thought is that these variations are not an artifact of finding the solution, but truly do exist in this theoretical circuit I have chosen.

Why?

A question that the reader may have after looking at all of this is “Why is the long-term structure important?” The answer lies in the fact that RLC circuits are embedded in many electronic devices, including radios and televisions. For this reason, it is important to know the current they put out. We don’t really want something that has an unpredictable output in devices that are high-cost.

Forward Plan

To further investigate the reason for the long-term structure, I will first solve for the constants in Equation [4] and plot the graphs of current again. Hopefully this will provide some insight into the workings of the circuit. I may also alter the initial parameters (inductance, resistance, etc.) to see if this provides any insight. If not, then I will investigate Mathematica’s differential equation solving techniques and attempt to alter my solution in a way that provides a more accurate solution.

Resources

1. Circuit Diagram Maker- http://www.circuit-diagram.org/

2. The RLC Circuit- University of British Columbia- http://www.math.ubc.ca/~feldman/m121/RLC.pdf

3. Mathematica Cookbook by Sal Mangano

Mathematica Notebook

https://drive.google.com/file/d/0B3mtB6CQNnpjejEzN25zbFlqajQ/edit?usp=sharing

Relativistic E&M: Preliminary Results

It is fairly easy to see that the electric and magnetic fields of various systems change drastically when considered in different reference frames. For example, consider a wire with a line of positive charges moving to the right at speed v, and an equal line of charges moving to the left at speed v.

This system has a net charge of zero, so there should be no electric field. However, the sum of the charges does cause a total current I = 2λv to the right, which gives a magnetic field of B = μ₀λv/πs in the ϕ direction (as dictated by the right-hand rule), for any distance s from the center of the wire.

Now, consider the same situation, but in the reference frame where q is at rest. Suddenly, the positive linear charge is much smaller than the negative one, leaving a net negative charge on the wire, which will produce an electric field. Simply by changing the reference frame, the situation switched from a purely magnetic phenomenon to a combination of electric and magnetic.

However, rather than trying to analyze the magnitude of the new charge and current values to find E and B, it is possible to simply use the following transformation equations to find out what the new E and B fields are.

$E’_x$ = $E_x$
$E’_y$ = $\gamma$ ($E_y$ – $vB_z$)
$E’_z$ = $\gamma$ ($E_z$ – $vB_y$)
$B’_x$ = $B_x$
$B’_y$ = $\gamma$ ($B_y$ + $\frac{v}{c^2}$ $E_z$)
$B’_z$ = $\gamma$ ($B_z$ – $\frac{v}{c^2}$ $E_y$)

Where $\gamma$ = $\frac{1}{\sqrt{1-{\frac{v^2}{c^2}}}}}$ (From Griffiths Introduction to Electrodynamics, 3rd Ed. p531). The only hiccup is that the original setup is in cylindrical coordinates, while the transformation equations are in Cartesian. However, Mathematica can do this automatically, so I’m going to leave it in these terms.

B-field: E-field:

The Mathematica file contains 3D vector plots of the E and B fields for the rest frame and a frame moving at v=0.25c, but so far, I haven’t figured out how to make it so that the user can vary the speed of the reference frame. Hopefully, I will figure that out soon. The key thing to note is that the model shows the interplay of E and B fields at relativistic speeds: the scenario starts out completely magnetic and ends up a mix of the two.

Preliminary Results: Modeling E and B Fields of a Toroidal Conductor to Explore Tokamak Plasmas

Thus far, I have determined values for the quantities of interest (except for $\mu$ of the plasma) and I have derived an expression for B and H. I will base the parameters of my model off of the Joint European Torus (as per Albanese, et al., 03; Crisanti, et al., 03). It appears that there will be no D field, since the plasma is a conductor and would not polarize, but simply experience a current.

$q(r) = \frac{r B_{\phi}(r)}{R B_{\theta}(r)} = 3$
$r = .95~m$
$R = 2.85~m$
$I = 6.0~MA$

I am going to assume that N, the total number of turns, is proportional to the safety factor: $N = \alpha q(r)$ where $\alpha$ will probably be related to the circumference of the torus (which can be found from the radii).

The Biot-Savart Law gives:

$d\textbf{B} = \frac{\mu_{0} \textbf{I} \times \textbf{r} dl}{4 \pi r^{3}}$.

If we assume that the torus is in the x-y plane, centered at the origin, and consider a test point at $\textbf{r}$ and source charge elements at various $\textbf{r’}$. Then $\scriptr = \textbf{r} – \textbf{r’}$. Consider a test point on the x-z plane.

Assuming that the winding is tight enough, we can say that $ \textbf{I} = I_{s} \hat{s} + I_{z} \hat{z}$ which, in cylindrical coordinates, is $(I_{s}cos(\phi), I_{s}sin(\phi), I_{z})$.

In evaluating the Biot-Savart Law, we have the term $\textbf{I} \times \textbf{r}$. Due to the symmetry of the tours, the x and z components cancel out, leaving just a y component. If the test point is in the x-z plane, this means that the magnetic field will be circumferential, or in the positive $\hat{\phi}$ direction. The magnetic field can then easily be found using Ampere’s Law:

$\textbf{B(r)} = \frac{\mu_{0} N I}{2 \pi s} \hat{\phi}$

for all points within the minor radius (inside the torus) and

$\textbf{B(r)} = 0$

for all points outside the torus.

From here, it is also easy to find the Auxiliary field, from $\textbf{H} = (1/\mu) \textbf{B}$, so

$\textbf{H} = \frac{1}{\mu} \frac{\mu_{0} N I}{2 \pi s} \hat{\phi}$

inside the torus and

$\textbf{H} = 0$

outside the torus, since there is no magnetic field.

I have also begun work on my Mathematica model. I began by trying to figure out how to get the vector field to look right, and have been working with a simplified version of my B equation, $\textbf{B} = k/r$. I have found that the transform to spherical coordinates is easiest to work with (since toroidal geometries do not fit easily into either spherical or cylindrical), which is why my expression uses r instead of s. This has given the following vector field:

The (simplified) circumferential magnetic field due to a toroidal solenoid (without taking into account the fact that the field is zero outside of the loop of the solenoid).

The vector field is the shape that I need it to be, but I’m having some trouble getting the field to be zero outside of the solenoid. I tried to use the piecewise function of Mathematica, but keep getting an error. I think I may need to define two fields (maybe 3) such that they cancel out in the regions where the field should be zero.

The next step will be to input the numbers into my expression, and work out the Mathematica model. Then I will be able to easily vary q(r) and observe the results.

Link to Mathematica notebook: https://drive.google.com/file/d/0B-C9MvBAfmyIQS12dTZJOGh5bm8/edit?usp=sharing

References

Raﬀaele Albanese, G Calabr`o, M Mattei, and F Villone. Plasma response models
for current, shape and position control in jet. Fusion engineering and design,
66:715–718, 2003.

F Crisanti, R Albanese, G Ambrosino, M Ariola, J Lister, M Mattei, F Milani,
A Pironti, F Sartori, and F Villone. Upgrade of the present jet shape and vertical
stability controller. Fusion engineering and design, 66:803–807, 2003.

Griffiths, D. J., & Reed College. (1999). Introduction to electrodynamics (Vol. 3). Upper Saddle River, NJ: prentice Hall.

Preliminary Results: C. elegans Diffraction Pattern Modeling

Staying true (so far) to my tentative project timeline, I acquired images of the C. elegans in various shapes, I have done quite a bit of research on Fourier Transforms and Fraunhofer Diffraction, and so far I have successfully transformed one image into the corresponding diffraction pattern.

IMAGE 1

I took this image and used mathematica to sharpen it –> setting it to grayscale and brighten it –> collect dimensional information –> apply a Fourier Transform, yielding (after some similar image manipulation):

This is a great diffraction pattern, but I had issues with the poor resolution and general image quality. To remedy this, I proceeded with images taken with a higher-resolution camera.

(full file for image 1: book 1 )

IMAGE 2

This beautiful image needed some manipulation, similar to image 1: I converted it to grayscale –> brightened it significantly (to make it a more definite shape, and to get rid of the “holes” in the luminescing nematode) –> collected image dimensions and data –> applied the FT. Unfortunately, I ran into a problem.

The produced image:

Obviously this is quite different than the first diffraction image.

I had a few hypotheses:

1. The image was saved as a .jpg, but the same image was produced when I tried again with a .png version of the image.

2. The computer is phase- shifting the image so that instead of the origin lying in the center of the product, it is splitting the right side from the left side and lining them up in the wrong order. How can I rearrange and correct the phase shift in the output?

An analogy to the second hypothesis:

—>

It is as if, instead of centering the origin in the center of the produced diffraction pattern, the computer is putting the “origin” in a different place, and splitting the image, similar to the parabola I produced above.

My solution is a little underhanded. I divided the image into four equal rectangles, and manually rearranged them to produce what I knew was the true image:

(full file for image 2: book 2a book 2b )

—————-

Reflection:

It is important to keep this process grounded: how is this relevant to Electromagnetism? The answer is that this entire process is only viable because of the laws of electromagnetism. I am analyzing the images by taking their Fourier Transforms. The diffraction pattern is the FT of the function that describes the electric field strength across the aperture of diffraction. In other words, I am applying an operation (the FT) to the image, which is a direct indication of the electric field strength across the aperture (the microscope slide) to mathematically find the diffraction pattern produced by the specific electric field array created by the shape of the worm.

Specifically, the diffraction pattern here is the Fraunhofer Diffraction pattern, or “far-field” diffraction, which occurs when the distances between the screen, aperture, and light source are appropriately far $L>>\frac{b^{2}}{\lambda}$. Diffraction effects are an outcome of the type of light wave.

It is also essential to realize what information is lost in the computation of these diffraction patterns. I am taking a real image, applying a FT to it, squaring the absolute value of the result, and arriving in a complex space. This process loses the phase information of the light, and as a result, it is possible to go from the image to the diffraction pattern, but impossible to find the image from the FT diffraction image.

Revised Project Plan: Relativistic E&M

So it seems that step 1 of my original plan is more involved than I thought. To satisfactorily derive the E- and B-field transformation equations, it would be necessary to delve into the depths of relativistic mechanics, including the transformation of equations for motion, momentum, and energy, among others. This seems like it is outside the scope of the project: indeed, Griffiths spends about 55 pages before he is able to state the field transformation equations. I thought there would be a point halfway through at which I could pick up and start the derivation, but I was incorrect, so I am going to take the transformation equations as given, and work from there.

That being said, my new timeline will be essentially the same as the old one, just starting at what used to be Step 2 with the application of the transformation equations to one or two situations.

1) 4/14-4/18: Pick one or two simple scenarios and find their E- and B- fields if they were traveling in a moving reference frame. This will be a computational step. The transformation equations are pretty straightforward, so it should take less time. This is just to have a proof of concept, so it is less important that the system has interesting behavior in a moving reference frame.

2) 4/18-4/24: Make 3D or 2D vector field models of these situations in Mathematica. This portion will be focused on figuring out how to make mathematica do what I want. The goal is to come up with an animation or interactive figure that can be used to view the vector fields when the system is moving at different speeds, starting at non-relativistic speeds and working up to the speed of light.

3) 4/24-5/2: Find and model situations that display either representative or unusual behavior when considered in a relativistic reference frame. Once the Mathematica simulation for the first situation has been figured out, the following cases should be easier to take care of. Interesting behavior might include systems that only have an electric field in one reference frame and only a magnetic frame in another. It also may be interesting to consider what happens if a reference frame is moving faster than the speed of light.

4) 5/15/14: Summarize results and write conclusions. This will consist of a final look at the systems considered earlier and suggest possible directions for future exploration.

Project Plan: Van Allen Belts

Summary:

The primary goal of my project is to create a 3d model of the shape and strength of the Earth’s magnetic field and define the locations of the Van Allen Belts within that model. According to the research I have done so far, a planetary magnetic field resembles the field of cylinder. Applying relevant Earth properties, I would then be able to create an initial model of the field. Furthermore, due to the proximity of these belts to the Earth, I will not have to take interactions with the solar wind into account when modeling the field. The modeling will be done with the Mathematica program. With the model complete, I would hope to compare it to other, more exact models of the Earth’s magnetic field to confirm the theoretical location of the Van Allen Belts. I would also be interested in noting if there is any relationship between core size of the planet and development of a magnetic field. My current research hasn’t turned up any leads for a mathematical way to approach this problem however.

Timeline:

•Week 1: (week of 4/6) Research the Van Allen Belts and Define Project Parameters -During this first week I plan to research the different possible facets of my project in order to determine the particular parameters I will be creating the 3d model with. This also includes looking for previously made 3d vector fields that can teach me how to plot the vector field in Mathematica. Furthermore I will be looking into some of the secondary objectives of my project to see if the ideas can be executed in a reasonable amount of time.

•Week 2: (week of 4/13) Creating the Initial 3D Model – During the second week of the project, we proceed onto the next step of creating our basic 3D magnetic field model. This 3D vector field model will be created using Mathematica and will create a visual representation of the Earth’s magnetic field. The initial model will be based off of the magnetic field of a cylinder, a design which has been suggested by multiple sources.

•Week 3: (week of 4/20) Finishing the Initial 3D Model and Model Comparisons – This week will be used to put any necessary finishing touches on the initial model and determine the location of the Van Allen belts within the model. I will also be comparing the model to observed data and other proposed models of the field. From these findings, I will be able to determine the accuracy of the field modeled in Mathematica. If the simple cylindrical model is not as accurate as predicted, this week will also be taken to edit the model and improve its accuracy.

•Week 4: (week of 4/27) Extended Modeling – During this week I will finish all alterations on a final edited model. If there is extra time, the current plan is to systematically alter the model to see how certain changes effect the magnetic field. Specifically my goal is to see if there exists some sort of correlation between the planet’s core size and the development of its magnetic field and subsequently its Van Allen Belts. If a correlation like this can be seen, the magnetic fields of other planets will be modeled and compared to actual data. This will allow us to confirm if the created model can be applied to other planets with only minor alterations to its coding.

•Week 5: (week of 5/4) Finishing Touches – During this week, any extra modeling will be quickly finished up and the rest of the week will be dedicated to organizing the collected data into a final presentation.

Sources:

Currently the sources I have browsed are:

http://www.phy6.org/Education/Iradbelt.html

http://vanallenprobes.jhuapl.edu/science/overview.php

https://www.spenvis.oma.be/help/background/traprad/traprad.html#APAE

http://www.nasa.gov/mission_pages/rbsp/main/index.html#.U0O-7fmIDlx

Project Plan: Modeling Mie Scattering in the Interstellar Medium (ISM) (adjusted)

Resources

Introduction to Electrodynamics, 4th ed. by David J. Griffiths
Physics of the Galaxy and Interstellar Matter by H. Scheffler and H. Elsässer
Interstellar Grains by N.C. Wickramasinghe
Physical Processes in the Interstellar Medium by Lyman Spitzer, Jr.
The scattering of light, and other electromagnetic radiation by Milton Kerker
Mathematica 9 Help Documentation Center (the most valuable resource!)

Project Description

I will be exploring Mie theory and modeling this type of scattering for particles present in the interstellar medium (ISM). There are a number of parameters that can be easily derived from applying Mie theory to the ISM, including an asymmetry parameter (g), extinction coefficients, albedo, and phase functions. I will focus first on modeling the asymmetry parameter (g), but time permitting, will continue onto other properties as I move into Week 3 – as stated in my timeline (below).

While the space between stars and galaxies appears quite vast and barren given only the access of our eyes fixed quaintly at ground level, the ISM is teeming with a variety of matter and electromagnetic waves. These regions are rich with gas (atomic and molecular), dust, and are permeated by electromagnetic waves, or radiation, from starlight (and occasionally other sources). Observations of various astrophysical phenomena show that along a given line of sight, their is “extinction” of this radiation. Scattering and absorption account for these observations and occur due to the presence of various dust grains within the ISM. This is where Mie scattering fits into modeling the asymmetry parameter (g), a measure of the fraction of light scattered in the forward direction. Our efforts towards modeling this relationship as well as the values of other dust grain properties such as size, composition, etc, begins with a preliminary comprehension of Mie’s work.

In 1908, Mie was working well before the substantially assistive mechanisms of modern computational modeling. Although his successors refined the theory of scattering (for spherical particles) over subsequent years, Mie’s initial work is fitting for the relatively fundamental level of analysis in this course. As Kerker explains (5), the basic scattering functions can be derived from a process whereby the proper Ricati-Bessel function is chosen and scattering coefficients are derived:

$a_n=\frac{\psi_n(\alpha)\psi'_n(\beta)-m\psi_n(\beta)\psi'_n(\alpha)}{\zeta_n(\alpha)\psi'_n(\beta)-m\psi_n(\beta)\zeta'_n(\alpha)}$

and

$b_n=\frac{m\psi_n(\alpha)\psi'_n(\beta)-\psi_n(\beta)\psi'_n(\alpha)}{m\zeta_n(\alpha)\psi'_n(\beta)-m\psi_n(\beta)\zeta'_n(\alpha)}$

where m indicates an index of refraction, $\psi_n$ and $\zeta_n$ (and their respective primes) are the Ricati-Bessel functions chosen, and $\alpha$ and $\beta$ are constants given by wave parameters (k, etc). These scattering coefficients are then combined with a mathematical tool called a “Legendre polynomial” to give amplitude functions for the scattering. Other parameters can then be derived once these functions are modeled.

Tools

Mathematica
LaTeX

Timeline

Week 1 (4/7 – 4/13)

I will refresh and further extend my knowledge of Mathematica and continue my research into the computational and theoretical aspects of Mie scattering in the context of the interstellar medium (ISM). As my project is computationally based, I will focus heavily on bridging the divide between my theoretical knowledge of scattering in the ISM and my work in Mathematica.

Week 2 (4/14 – 4/20)

For Week 2 I plan on completing a working Mathematica model for the asymmetry parameter, g, and complimenting this work as needed with research into Bessel and Ricati-Bessel functions. Mie theory is founded in the rigors of these functions and gives solutions to Maxwell’s equations that illustrates the scattering of waves by spherical particles. Specifically useful with the Bessel and Ricati-Bessel functions are the eponymous differential equations. If this work is completed I will move on to Week 3 work.

Week 3 (4/21 – 4/27)

I will continue modeling. My initial research into the theory will be added to as needed. As time permits, I will continue on to explore the utility of Mie theory and scattering within the ISM as it relates to the derivation of other interstellar grain properties.

Week 4 (4/28 -5/4)

I will finalize any lingering modeling. My results will be nearly all in and I will begin to wrap up my blog – focusing on visualizations (plots and animations) and ensuring that they function properly within the blog space. This week will be mainly devoted to polishing off my blog posts (data and results especially), i.e. making all aspects of the blog look aesthetically pleasing.

Week 5 (5/5 – 5/11)

This week concludes my project as I finish commenting on my peer’s blog posts.

Collaborators

While I plan on working alone, Professor Magnes will be assisting and advising as this project progresses. Both of my predecessors focused on the theory and modeling of Rayleigh scattering – a related phenomena but still outside of the purview of my project. I intend to move in a direction much different than my predecessors who explored scattering of the Rayleigh domain. I do, however, anticipate that as my project develops, I will be reflecting on my results and the possibility exists to compare and contrast them in the context of the work done by these individuals. I cannot predict what these comparisons may entail, but as I conclude my project, these ties may reflect elements shared between background theory, computational processes, and my results.

Project Plan: A Guide To Convolution In Action

Description of project

Convolution is the theory behind interpreting the data presented. When physicists use optical tools for their experiments they need to understand whether the optics they are using will transmit the proper information. In practice one is limited to the material of the filters, as the wave fronts get distorted by the material they pass through. In order to be able to work with what you have, physicists model their possible optics layout before purchasing the optics. To retrieve the desired information physicists model the convoluted wave front, and then prepare a good deconvolution mechanism that in practice should yield the necessary data. This project is an attempt to understand convolution and deconvolution of electromagnetic waves through optical filters. I will be exploring the theory behind convolution, demonstrate examples of convolution, attempt deconvolution of a convoluted distributions, and then hopefully show a real world example of actual optical filters.

Theory

Convolution is the mixture of functions that individually have known Fourier transforms. A Fourier transform is the transformation of a square-integrable function $f(x)$ from one domain to another (5). It is defined as such:

$f(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty }^{\infty }\!\Phi(k)e^{ikx}dk \qquad \Phi(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty }^{\infty }\!f(x)e^{-ikx}dx$

Both the function and the Fourier transform describe the same system though under different but related spaces (See: Plancherel’s Theorem). The advantage is if you have a machine that measures time but you are trying the measure the system as a function of frequency, then you can measure the system with that machine and simply take the Fourier transform of your data. Unfortunately, the deviations of the Fourier pairs are bounded by the uncertainty principle. A function with a narrow spread will yield a transformation with a wider spread, and vice versa.

$\sigma^2_\Psi\sigma^2_\Omega\geq\left(\frac{1}{2i}\langle[\hat{\Psi},\hat{\Omega}]\rangle\right)^2$

where $\hat{\Psi}$ and $\hat{\Omega}$ are two arbitrary operators, and $\sigma_{i}$ is the standard deviation.

The definition of a convolution of two functions is defined as follows:

$f_{1}(x)\ast f_{2}(x)=\int_{-\infty }^{\infty }\!f_{1}(x')f_{2}(x-x')\mathrm{d}x' \\ \\ \Phi_{1}(k)\ast \Phi_{2}(k)=\int_{-\infty }^{\infty }\!\Phi_{1}(k')\Phi_{2}(k-k')\mathrm{d}k'$

The convolution theorem then states that the Fourier transform of a convolution is the product of the Fourier transforms to a factor of $\sqrt{2\pi}$ . Similarly, the Fourier transform of a product of functions is the convolution of the Fourier transforms (5):

${\widehat_{f_{1}\ast f_{2}}} (x)= \sqrt{2\pi}\;{\Phi_1}(k)\cdot {\Phi_2}(k) \qquad {\widehat_{f_{1}\cdot f_{2}}} (x)= \frac{1}{\sqrt{2\pi}}\;{\Phi_1}(k)\ast {\Phi_2}(k)$

The implication of this theorem is if any arbitrary curve can be expressed as a product of functions with given Fourier counterparts, then it can undergo deconvolution to yield the desired data as represented by known functions (3).

$f_{1}(x)\ast f_{2}(x)\rightleftharpoons \Phi_{1}(k)\cdot \Phi_{2}(k)$

Timeline

All work will either be done on my computer or at the sci-vis lab.

Week 1: I will become familiar with Professor Magnes’s MATLAB script and reconstruct it in Mathematica. I will use the information provided for me in the texts to create new examples of various convoluted distributions. I will also provide an introduction to the theory that pertains to my project.

Week 2: By now I should be familiar enough with Mathematica to display some cool examples. I will attempt to provide an example of real world convolution of two optical filters from thorlabs. In practice convolution of two actual filters is not as easy as adding two equations. I will need to figure out how to generally apply my ideal examples to sets of data.

Week 3: I will now attempt to demonstrate the deconvolution of a distribution. I will show this by using one of my previous examples. In theory I should be able to demonstrate proper deconvolution of two functions.

Week 4: Now that I have demonstrated deconvolution, I should be able to demonstrate deconvolution of the data I had previously showed in convolution form. This would be very tricky but hopefully I should be able to succeed.

Week 5: I may be setting the bar up too high, so possibly some of my work will take more time than expected. I should be finished with everything now. Here I will tweak my project, and conclude my demonstration.

Note: I may stray from my timeline, but that is only because I got caught up in an interesting phenomenon. Should I decide to alter my direction, I will update my timeline accordingly.

Resources

Will be updated if necessary

(1) Griffiths, David J. Introduction to Electrodynamics. Upper Saddle River, NJ: Prentics Hall, 1999. Print.

(2) Hecht, Eugene. Optik. München: Oldenbourg, 2001. Print.

(3) James, J. F. A Student’s Guide to Fourier Transforms: With Applications in Physics and Engineering. Cambridge: Cambridge UP, 2011. Print.

(4) Pedrotti, Frank L., Leno S. Pedrotti, and Leno Matthew. Pedrotti. Introduction to Optics. Upper Saddle River, NJ: Pearson Prentice Hall, 2007. Print.

(5) Sadun, Lorenzo Adlai. Applied Linear Algebra: The Decoupling Principle. Providence, RI: American Mathematical Society, 2008. Print.

Question to the reader: Is the verb of deconvolution: deconvolve or deconvolute?

Project Plan: RLC Circuits

Plan/Goals:

In this project, I plan to study the relevant differential equations that govern RLC circuits and use Mathematica to solve them for values that are useful. The general equation governing a basic RLC circuit with a capacitor, voltage, resistor, and inductor in series, in that order is:

$LI'(t)+RI(t)+\frac{1}{C}Q(t)=V(t)$ [Equation 1] (UBC- Source 4)

which, when going through a series of substitutions, becomes:

$LI''(t)+RI'(t)+\frac{1}{C}I(t)=\omega E_{0}cos(\omega t)$ [Equation 2] (UBC- Source 4)

Equation 1 has six variables: L (inductance), R (resistance), C (capacitance), V (voltage), Q (charge), and I (current). When a circuit like this is set up in the lab, the values that are known are L, R, C, and V because they directly depend on the components of the circuit. Once the differential equation [2] is solved, values for current (I) and charge (Q) can be determined. I will use Mathematica to solve for the general solution to this differential equation [2], which is a second-order differential equation. Once I have the general solution, I will vary the initial conditions to determine the effect of different circuit components on the overall properties of the circuit. Following this, I will develop more series RLC circuits with components that are set up differently in terms of their component structure.

Timeline (Weeks 1-5):

Week 1: I will begin by reviewing basic differential equation solving techniques for first and second order differential equations. I will also study the differential equation solving capabilities of Mathematica and review the techniques for solving second-order differential equations as they apply to RLC circuits.

Week 2: I plan on solving for the general solution to Equation 2 above (using Mathematica). I will vary different initial conditions and create graphs that visualize the changes that occur. I will also have a visual representation of the circuit.

Week 3: Develop another series circuit or study a previously built one. Determine the general equation for it and begin the solution process.

Week 4: Finalize the solution for the second circuit. Develop graphs for visualization purposes.

Week 5: I will finalize my project by proofreading all the components and making sure everything is presentable. I will also provide constructive criticism to my peers on their projects.

Sources:

1. Mathematica Cookbook by Sal Mangano

2. Electronic Circuit Analysis for Scientists by James A. McCray and Thomas A. Cahill

3. Dynamical Systems with Applications using Mathematica by Stephen Lynch

4. The RLC Circuit- University of British Columbia- http://www.math.ubc.ca/~feldman/m121/RLC.pdf

5. Class Notes- Mathematics 228 (Methods of Applied Mathematics) taught by Matthew Miller

Collaborators:

N/A

Project Plan: Relativistic E&M

Sources: In terms of sources, this project is fairly simple. The main source will be Chapter 12 of Griffiths’ Introduction to Electrodynamics, 3rd ed. This will provide a framework for deriving the transformation equations.

Process/Timeline: There are five main steps involved in this project:

1) 4/7-4/14: Derive the transformation equations. This will be a proof-based step, and I need to refresh myself on some of the concepts of mechanical relativity, so it may take some time.

2) 4/14-4/18: Pick one or two simple scenarios and find their E- and B- fields if they were traveling in a moving reference frame. This will be a computational step. The transformation equations are pretty straightforward, so it should take less time. This is just to have a proof of concept, so it is less important that the system has interesting behavior in a moving reference frame.

3) 4/18-4/24: Make 3D or 2D vector field models of these situations in Mathematica. This portion will be focused on figuring out how to make mathematica do what I want. The goal is to come up with an animation or interactive figure that can be used to view the vector fields when the system is moving at different speeds.

4) 4/24-5/2: Find and model situations that display either representative or unusual behavior when considered in a relativistic reference frame. Once the Mathematica simulation for the first situation has been figured out, the following cases should be easier to take care of. Interesting behavior might include systems that only have an electric field in one reference frame and only a magnetic frame in another. It also may be interesting to consider what happens if a reference frame is moving faster than the speed of light.

5) 5/15/14: Summarize results and write conclusions. This will consist of a final look at the systems considered earlier and suggest possible directions for future exploration.

Modeling and Experimental Tools with Prof. Magnes

Ideal for getting ideas and feedback on upper level physics tools.

Category Archives: Spring 2014

Preliminary Results- RLC Circuits

Relativistic E&M: Preliminary Results

Preliminary Results: Modeling E and B Fields of a Toroidal Conductor to Explore Tokamak Plasmas

Preliminary Results: C. elegans Diffraction Pattern Modeling

Revised Project Plan: Relativistic E&M

Project Plan: Van Allen Belts

Project Plan: Modeling Mie Scattering in the Interstellar Medium (ISM) (adjusted)

Project Plan: A Guide To Convolution In Action

Project Plan: RLC Circuits

Project Plan: Relativistic E&M