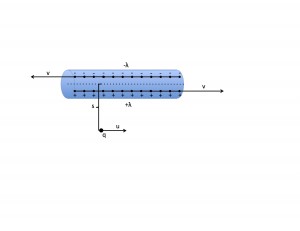
It is fairly easy to see that the electric and magnetic fields of various systems change drastically when considered in different reference frames. For example, consider a wire with a line of positive charges moving to the right at speed v, and an equal line of charges moving to the left at speed v.

This system has a net charge of zero, so there should be no electric field. However, the sum of the charges does cause a total current I = 2λv to the right, which gives a magnetic field of B = μ₀λv/πs in the ϕ direction (as dictated by the right-hand rule), for any distance s from the center of the wire.

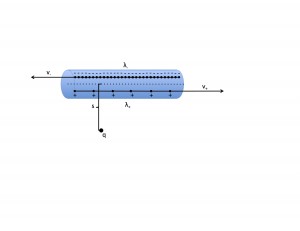
Now, consider the same situation, but in the reference frame where q is at rest. Suddenly, the positive linear charge is much smaller than the negative one, leaving a net negative charge on the wire, which will produce an electric field. Simply by changing the reference frame, the situation switched from a purely magnetic phenomenon to a combination of electric and magnetic.

However, rather than trying to analyze the magnitude of the new charge and current values to find E and B, it is possible to simply use the following transformation equations to find out what the new E and B fields are.

$E’_x$ = $E_x$
$E’_y$ = $\gamma$ ($E_y$ – $vB_z$)
$E’_z$ = $\gamma$ ($E_z$ – $vB_y$)
$B’_x$ = $B_x$
$B’_y$ = $\gamma$ ($B_y$ + $\frac{v}{c^2}$ $E_z$)
$B’_z$ = $\gamma$ ($B_z$ – $\frac{v}{c^2}$ $E_y$)

Where $\gamma$ = $\frac{1}{\sqrt{1-{\frac{v^2}{c^2}}}}}$ (From Griffiths Introduction to Electrodynamics, 3rd Ed. p531). The only hiccup is that the original setup is in cylindrical coordinates, while the transformation equations are in Cartesian. However, Mathematica can do this automatically, so I’m going to leave it in these terms.

B-field: E-field:

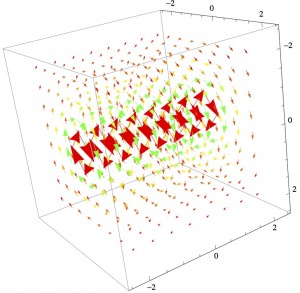
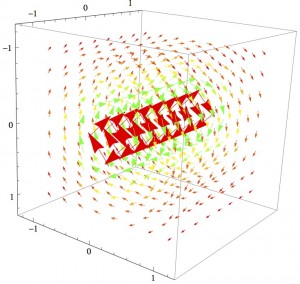
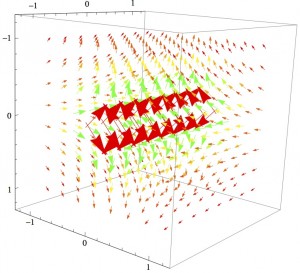
The Mathematica file contains 3D vector plots of the E and B fields for the rest frame and a frame moving at v=0.25c, but so far, I haven’t figured out how to make it so that the user can vary the speed of the reference frame. Hopefully, I will figure that out soon. The key thing to note is that the model shows the interplay of E and B fields at relativistic speeds: the scenario starts out completely magnetic and ends up a mix of the two.