Project Plan (revised)

C. elegans Diffraction Pattern Modeling

Sources & Resources

  1. Introduction to Electrodynamics, D. Griffiths
  2. A Student’s Guide to Fourier Transforms, J. F. James (chapters 1 and 9)
  3. Past work by Professor J. Magnes and her assistants
  4. C. elegans nematodes, property of Professor K. Susman, photos taken by her laboratory assistants
  5. Introduction to Optics, 3rd edition, Pedrotti & Pedrotti & Pedrotti (chapter 11)

Necessary steps & what I plan to model

  • Take photos of the C. elegans with the Insight Camera (directly from the microscope)
  • Manipulate the photos (remove noise) using Mathematica
  • Take the Fourier transform of the photos to discover the diffraction pattern
  • ( |Fourier Transform|2 = the diffraction pattern)

Collaborators

I will be working alone, but with Professor K. Susman’s worms and equipment, and Professor J. Magnes’ old work as a reference. I also will be receiving some training in using the microscope’s camera attachment (most likely from one of Professor Susman’s lab assistants).

Tentative Timeline

Starting with week1= April 6-12 (Sunday to Saturday):

Week1: I plan to take photos (if I get permission from Professor Susman), and work on an algorithm for generating reliably noiseless photos. I plan to become comfortable with Fourier transforms on Mathematica, and take some preliminary transformation models.

Week2: From now on, it is going to progress in a semi-continuous fashion. This week I plan to continue working with the Fourier transforms on Mathematica, making improvements to the algorithm and recording the changes. Keeping in mind the goal of this project, it is important to take note of the models in the context of electromagnetic waves. It is also important to keep careful track of the data, and make sure the images are clear and easy to see.

Week3: By now I expect to have some good images. I will continue to improve on them, and possibly will begin resorting to doing the matrix multiplication “by hand” on Mathematica. I hope to have a very good understanding of Fourier transforms of images by the end of this project.

Week4: Now that I hopefully have good images corresponding to several shapes of C. elegans, I hopefully will be able to begin adding at least a small volume of genuinely good data to the Diffraction Symmetries Library.

Week5: In the final week, I will make some final touches to the library. Even though it is primarily about the data, I hope to polish the presentation and add any necessary comments. 

Some Preliminary Information

It is important to discuss what I already have knowledge of: I already know how to grow worms (how to transfer them to new E. coli food dishes so they can reproduce). I have a general idea how to take Fourier Transforms by hand, and what they generate. I do not know how to take a Discrete Fourier Transform of an image, and I do not know how to do it with matrix multiplication. I also know very little about electromagnetic Fraunhofer diffraction.

Some Essential Relationships

The crux of my thesis:

(1)   \begin{equation*}\left|FT|\right^2=Diffraction Pattern\end{equation*}

Basic Fourier Transform equation:

(2)   \begin{equation*} F(t)= \int_{-\infty}^{\infty} \Phi (v) {e }^{2 \pi i v t } dv \end{equation*}

(3)   \begin{equation*} F(t) \leftrightarrow \Phi (v) \end{equation*}

Discrete Fourier Transform in matrix form:

(4)   \begin{equation*}\begin{bmatrix} A(0)\\ A(1)\\ A(2)\\ ...\\ A(N-1) \end{bmatrix} = \begin{bmatrix} 1&1&1&...&1\\ 1&e^(\frac{2 \pi i}{n})&e^(\frac{4 \pi i}{n})&...&e^(2(N-1)\frac{\pi i}{n})\\ 1&e^(\frac{4 \pi i}{n}) &e^(\frac{8 \pi i}{n}) &...& e^(4(N-1)\frac{\pi i}{n})\\ ... & ... & ... & .... &...\\ 1 & ... & ... &...& e^((N-1)^2(\frac{\pi i}{n})) \end{bmatrix} \begin{bmatrix} a(0)\\ a(1)\\ a(2)\\ ...\\ a(N-1) \end{bmatrix} \end{equation*}

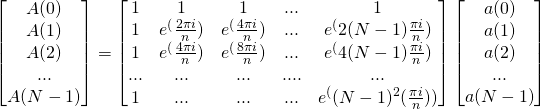
(It can be noted that this matrix multiplication requires $N^2$ multiplications. The Fast Fourier Transform (FFT) method, which can only be run by computing machines, reduces the number of multiplications from $N^2$ to $2Nlog_2(N)$.

Share

1 thought on “Project Plan (revised)”

  1. Avatar photoJenny Magnes

    It is important to keep in mind that it is the FT of the electric field that is used in the construction of diffraction patterns. How is your motivation met by this modeling exercise?

Comments are closed.