For the second week of this experiment I chose to begin my analysis by focusing in on a topic I believe I’ve glossed over thus far: orbital resonance. What I have neglected to mention is that this “resonance” is a ratio of the orbital periods for two objects rotating around the same central body of mass, and is related to the orbital radii of the object. To start with an example relevant to this project, the orbital period of an asteroid located at the 2/1 resonance point with Jupiter will be one half that of Jupiter’s, so it will complete two orbits for every one Jupiter completes. The relation between orbital period and orbital radii is given by Kepler’s Third Law, that the ratio
where P is orbital period and a is orbital radius is a proportion that holds for any object rotating around the Sun. This was used to calculate the location of the 2/1 resonance at 3.27 AU, knowing the orbital radius of Jupiter to be 5.2 AU and the using a ratio of periods as 2:1 for Jupiter:asteroid. We also can use the equation for orbital speed to calculate initial velocity of an object at a certain orbital radii:
where G is the gravitational constant, M is the mass of the Sun, and r is the orbital radii. I used a value of 39.5 for G with time in years, distances in AU, and masses in solar masses for simplification; we already know the distance is AU, and the mass of the Sun in solar masses is, obviously, 1. This is very useful to this simulation, in terms of understanding that the initial values chosen in the system are not arbitrary; significant deviations could lead to the code breaking. It is also helpful to us for calculating the initial conditions for an asteroid at another radii in resonance with Jupiter, or a Kirkwood gap. This week I added asteroids around the 3/1 resonance radii. Using Kepler’s Law as stated before, this orbital radius was calculated to be about 2.5 AU (which matches the known value) for an initial orbital velocity of 3.97 AU/yr. I also placed two asteroids both closer and farther to the Sun for comparison. I am also including the orbital graphs for the 2/1 resonance from last week as comparison.
For some reason, the orbits of the asteroids around the 3/1 resonance is even more irregular, perhaps caused by perturbations from planetary bodies other than Jupiter- namely, the Earth or the Sun. In the next week I will be analyzing what causes this stark change in orbit.
For my precession of the perihelion of Mercury program, I added the ability to calculate the position of the semi-major axes by surmising that on these axes not only will the perihelion lie, but the rate of change in radius will be small because the orbit becomes more elliptical, rounds out, and slows down. This assumption is based on Kepler’s Second law, that a line joining a planet and the Sun sweeps out equal areas during equal intervals of time; if the radius is largest here, it will be sweeping over more area, so the planet will move more slowly at these points. The position is then converted from Cartesian coordinates to polar coordinates. I then plot time against the position angle theta, take a linear fit through the data points, and take the slope to be the rate of precession. Afterwards, looping over an interval of alpha values, I will plot alpha against the precession rate, fit the data points, and take the slope to be the rate of precession. Unfortunately, when I tried to plot time against the angle theta, I kept receiving a value of close to 0 for the precession rate (slope). Without this slope, I am unable to calculate the precession rate for any values of alpha, and therefore cannot yet compare to the theoretical or expected value for the precession rate. I need to spend the next week debugging and figuring out how to make this program output the data I want it to.
https://docs.google.com/document/d/1UBlg3d4G4RBf1pFgHE8AO1PzGjMjqwBs2hGTOAQ3FY4/
https://docs.google.com/document/d/1_GCUtQHpeSyNeQlUyF8ofSNFEFvcEyW8BAWswCMKjQ4/

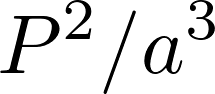
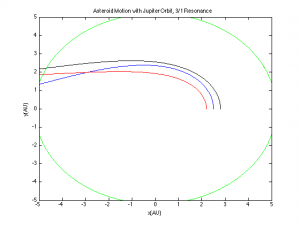

On the orbital ratio: Are these the orbits about the asteroid about Jupiter and Jupiter about the Sun? What kind of results do you expect? It would be nice to have captions for your figures to explain and point out the important parts of your figure. It is always a good idea to have someone else read your work over before publishing to avoid grammatical and punctuation issues. Can you give access to your code?