Experimental vs. Theoretical Values
It was immediately apparent when I began collecting data for this experiment that the equations I derived to anticipate voltage and frequency values were not entirely accurate. Here I will calculate expected curve shapes and expected values of frequency and decay, and and compare them to experimentally measured values. The majority of the difference in theoretical vs measured data is the fact that there is some resistance in the circuit. It may be possible to discover this resistance from the future tests, if not from the current data.
Shape Of Potential Curve
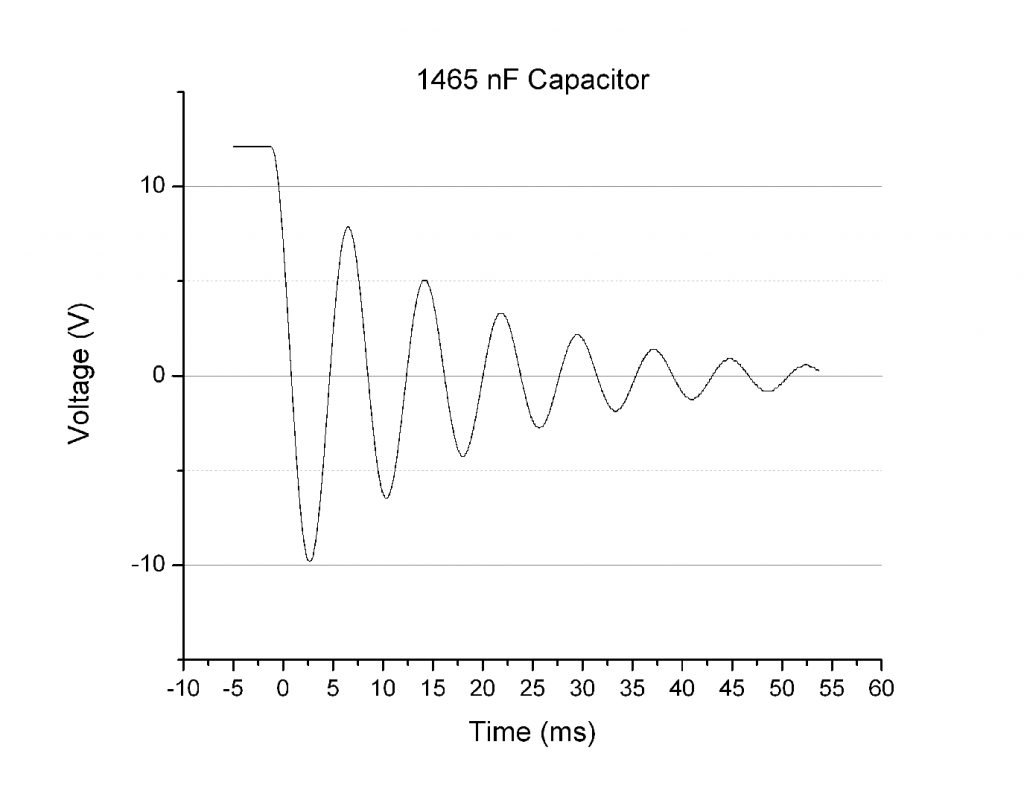
Figure 1. 1465 nF Capacitor and 996 mH Inductor in series.
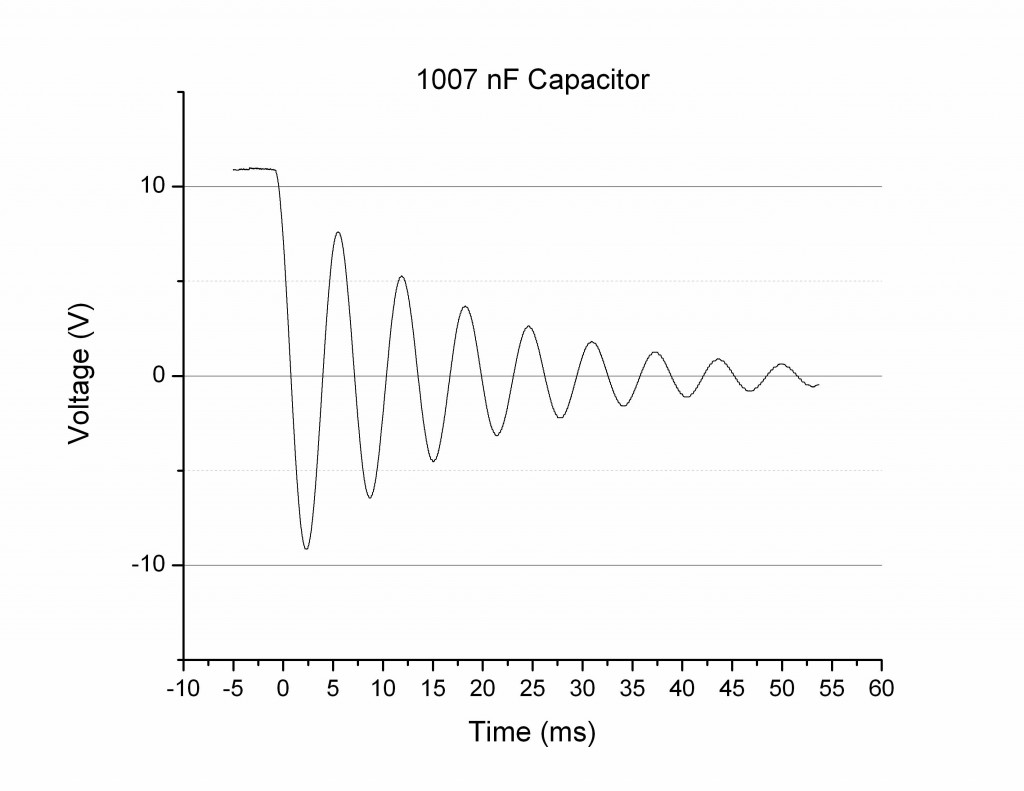
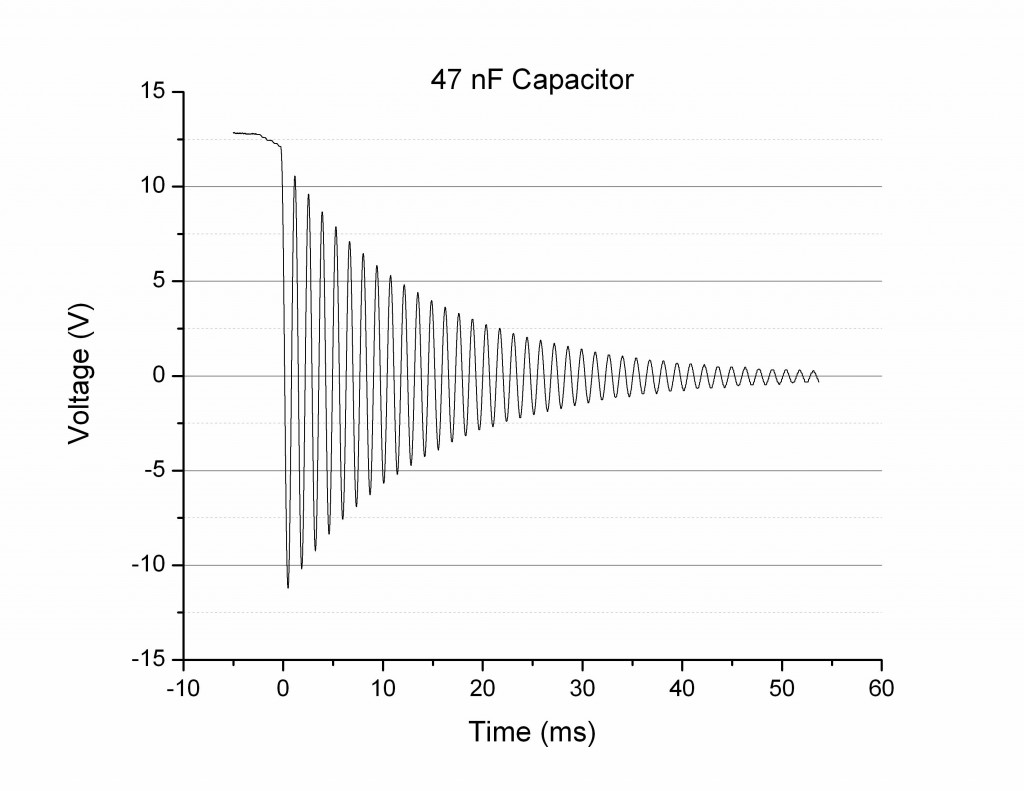
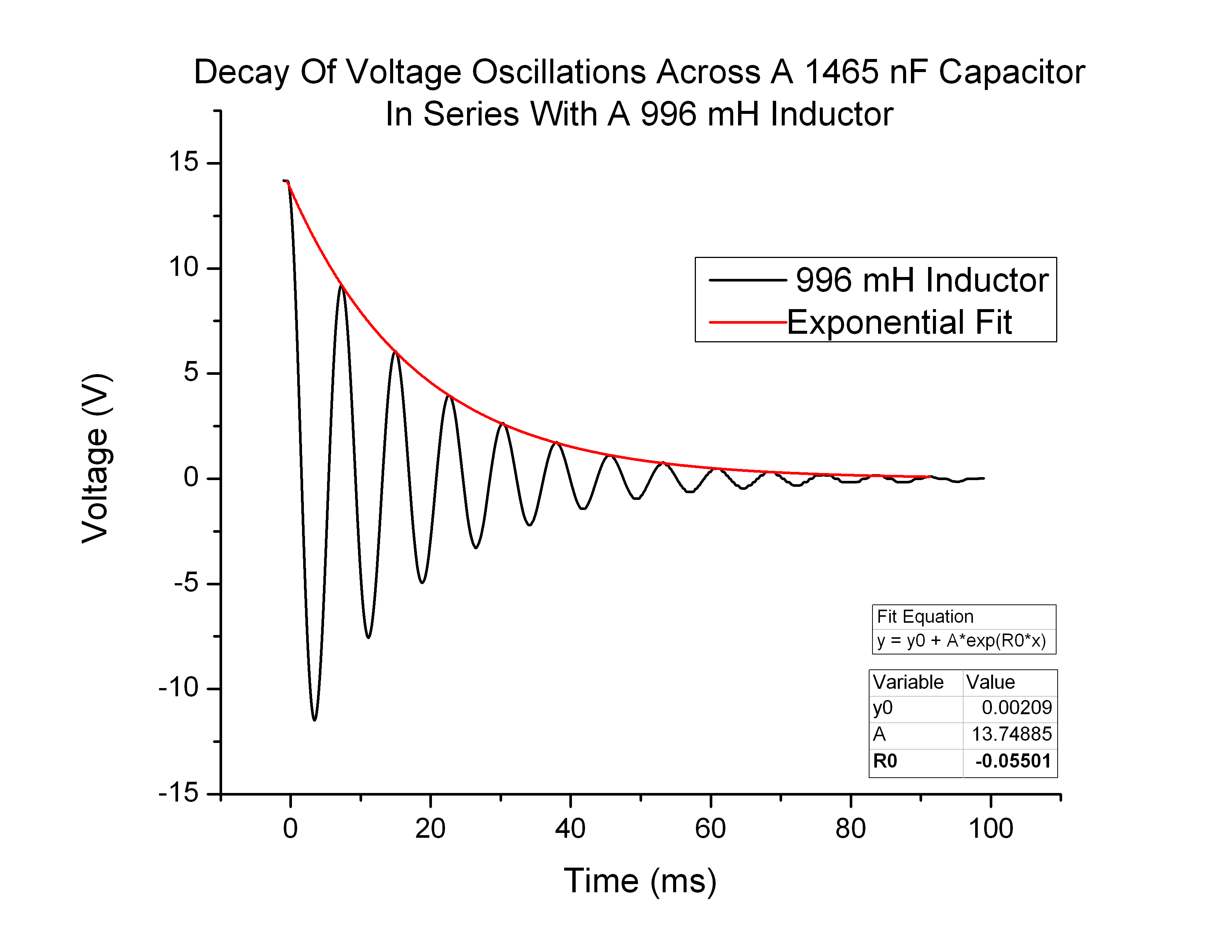
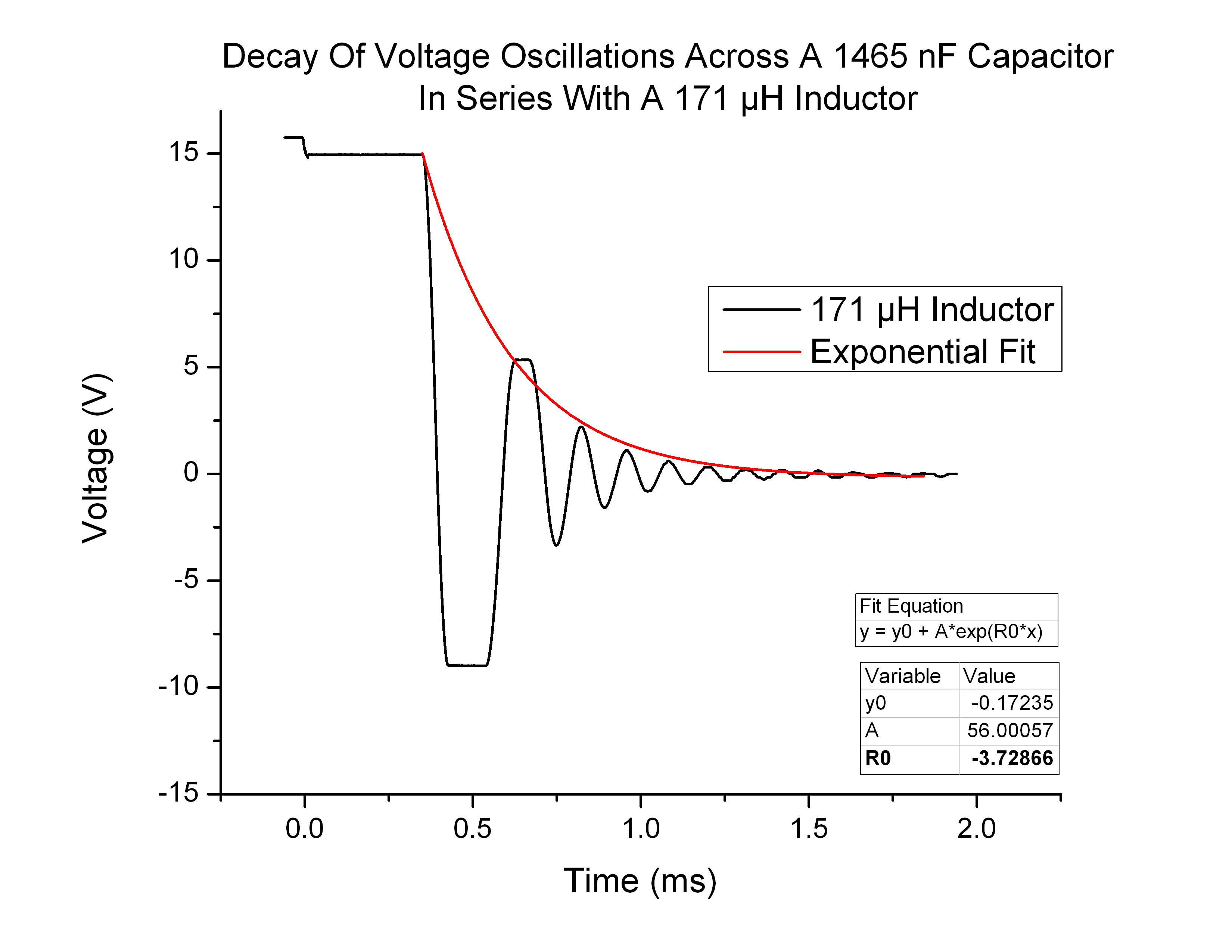
In theory, the circuit I constructed was a LC circuit. This means there was no resistor in series with the capacitor and inductor components, and that the wires have negligible resistance. Theoretically the oscillations of the voltage after the capacitor discharged through the inductor should continue indefinitely. This is analogous to how an object on a spring would oscillate forever without drag/friction forces acting upon it. That being said, it is readily apparent that the oscillations did not continue indefinitely. In fact they took around a 10th of a second to dissipate (in the case of the 1465 nF capacitor and 996 mH inductor circuit above). This means that there is damping occurring on the oscillations. So while theoretically I built an LC circuit, experimentally it behaved more like a damped LC circuit, or an RLC circuit, as if there was a resistor in series with the capacitor and inductor. This means that the relevant governing equation was not 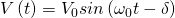 , but rather
, but rather 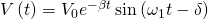 . Below (Figure 2) is the demonstration of expected shape (red) and measured shape (blue) of the voltage curve vs time as seen in my “Preliminary Data” post:
. Below (Figure 2) is the demonstration of expected shape (red) and measured shape (blue) of the voltage curve vs time as seen in my “Preliminary Data” post:
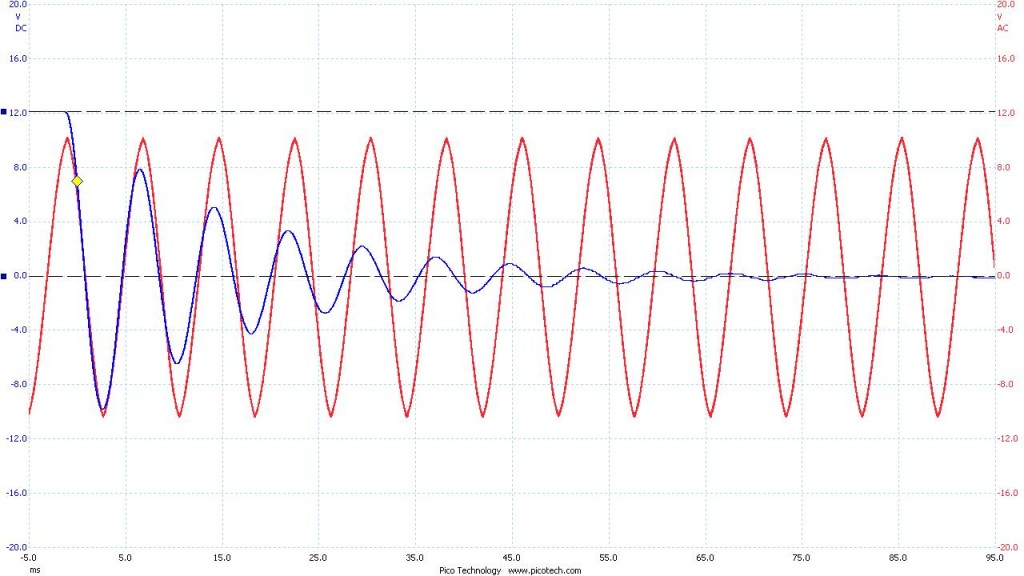
Figure 2
Frequency
To review,
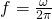 (1)
(1)
In Simple Harmonic Motion
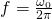 ;
; 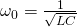 . (2)
. (2)
But as we just discussed, because the circuit is not ideal and has an equivalent resistance, these oscillations are actually described by Damped SHM, the equations being as follows:
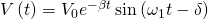 (3)
(3)
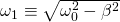
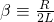 (4)
(4)
Thus
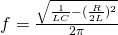 (5)
(5)
Where, solving for R, we can estimate the equivalent resistance of the circuit:
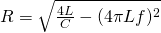 (6)
(6)
Below is a table of values (Figure 3). On the left are all of the the experimentally measured values from this project. The expected theoretical frequency was calculated using Equation (2). The resistance of the circuit was estimated using Equation (6).
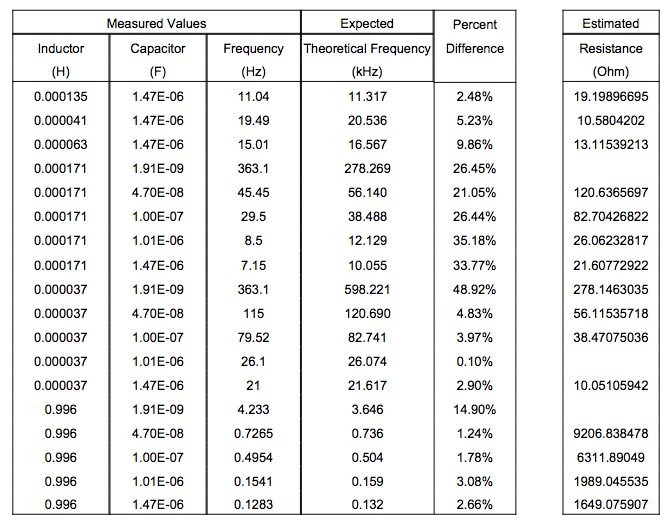
Figure 3
While the measured frequencies are not always very close to the predicted value, they are all well within an order of magnitude of each other, meaning the relationship defined by Equation (2) is clearly evident.
The estimated values of resistance, on the other hand, are extremely improbable. The resistivity of small connection wires is on the order of 10^-2 Ohms or lower. This indicates either a mistake in my derivation of resistance as a function of capacitance, inductance, and frequency, or a relationship that I don’t quite understand. It is possible that the equivalent resistance of the circuit changes as a function of voltage, or the change in current, in a way I do not know about.
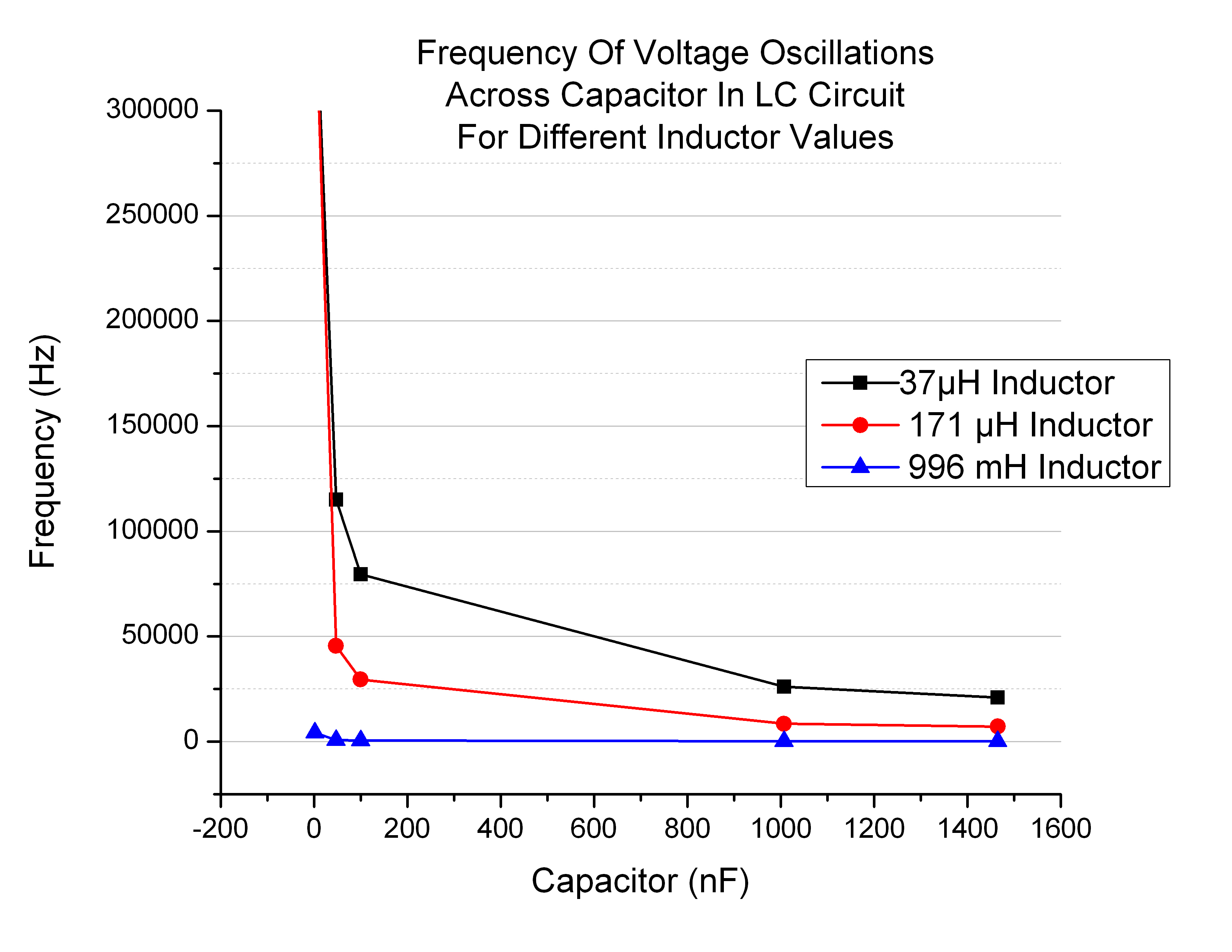
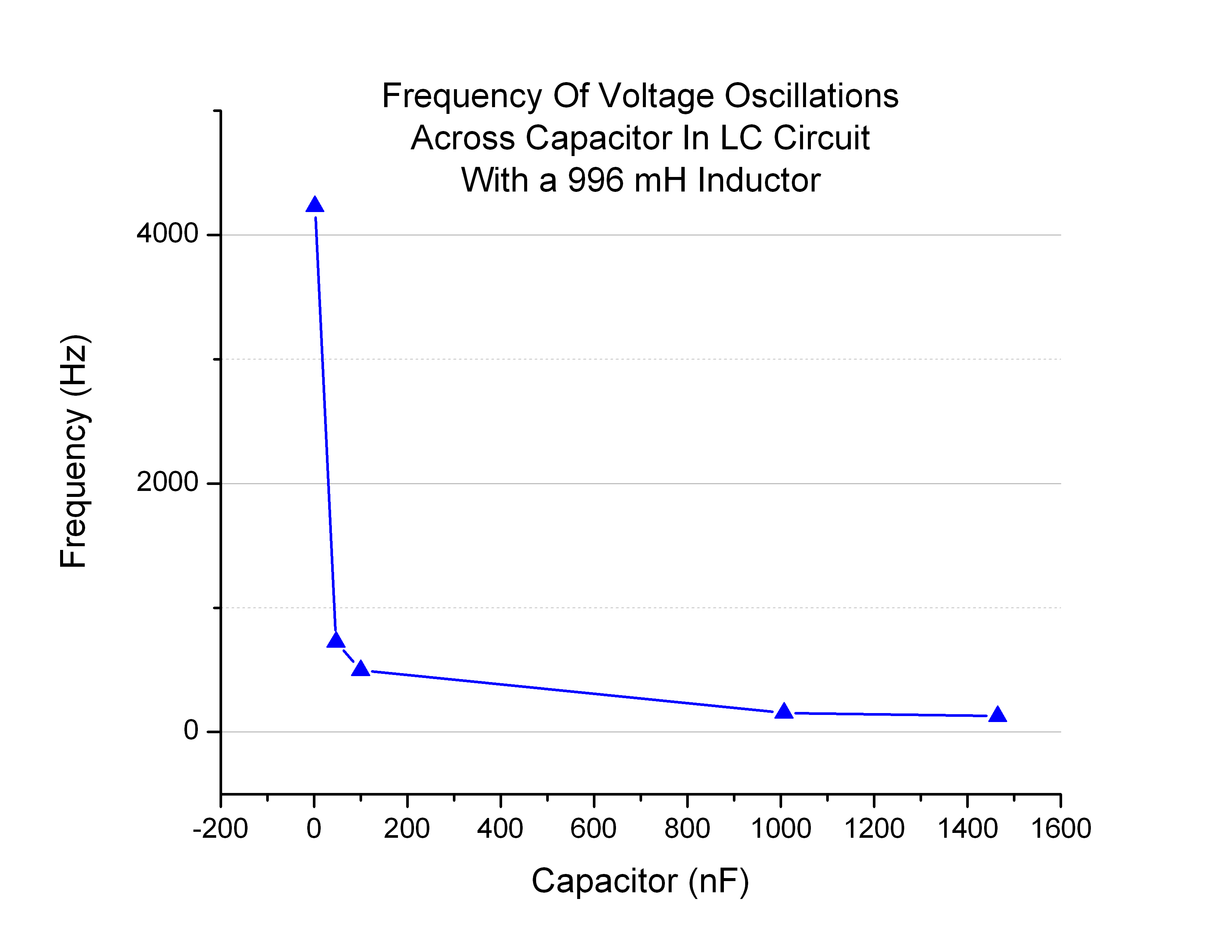
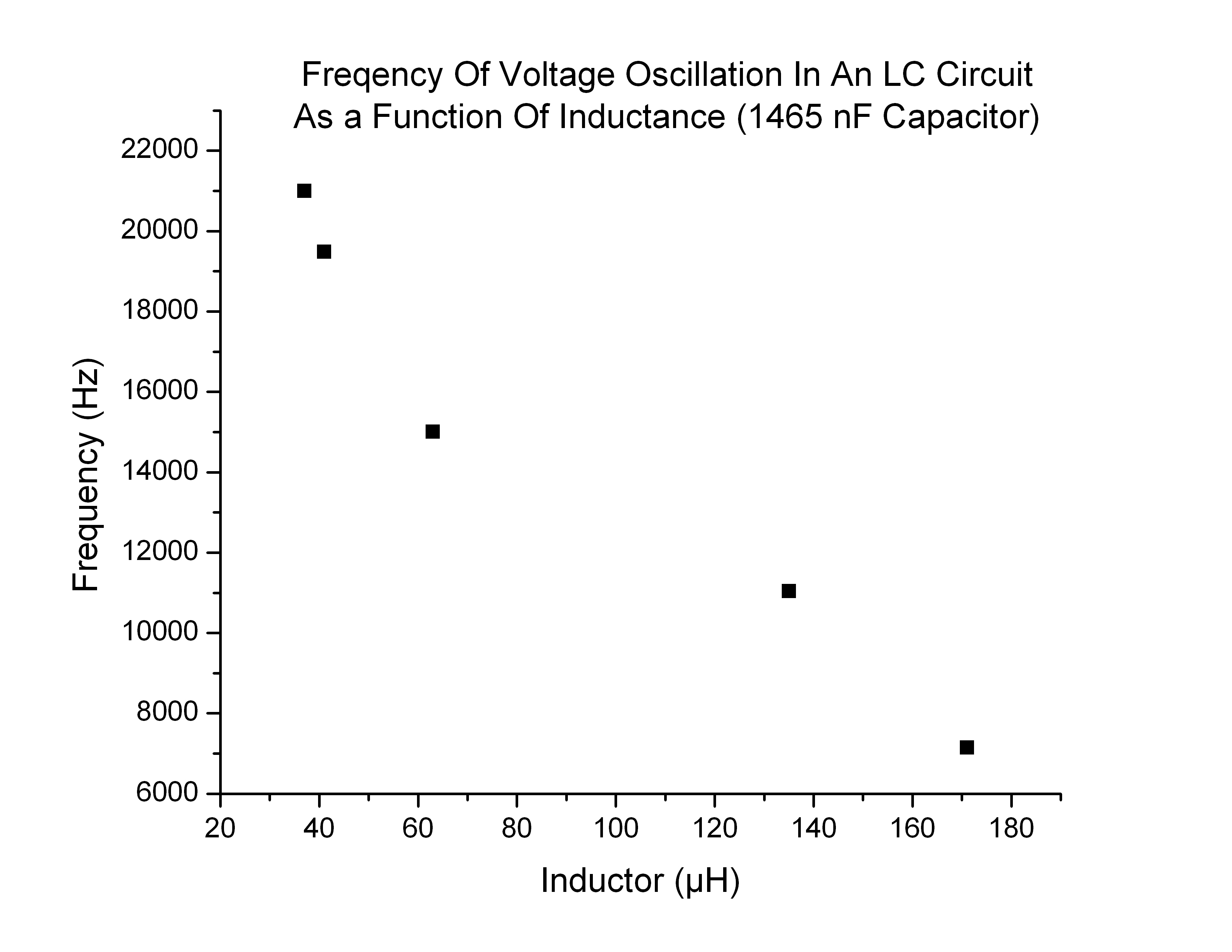
Overall, the graphs of frequency as a function of L or C (Figure 4) were the correct shape.
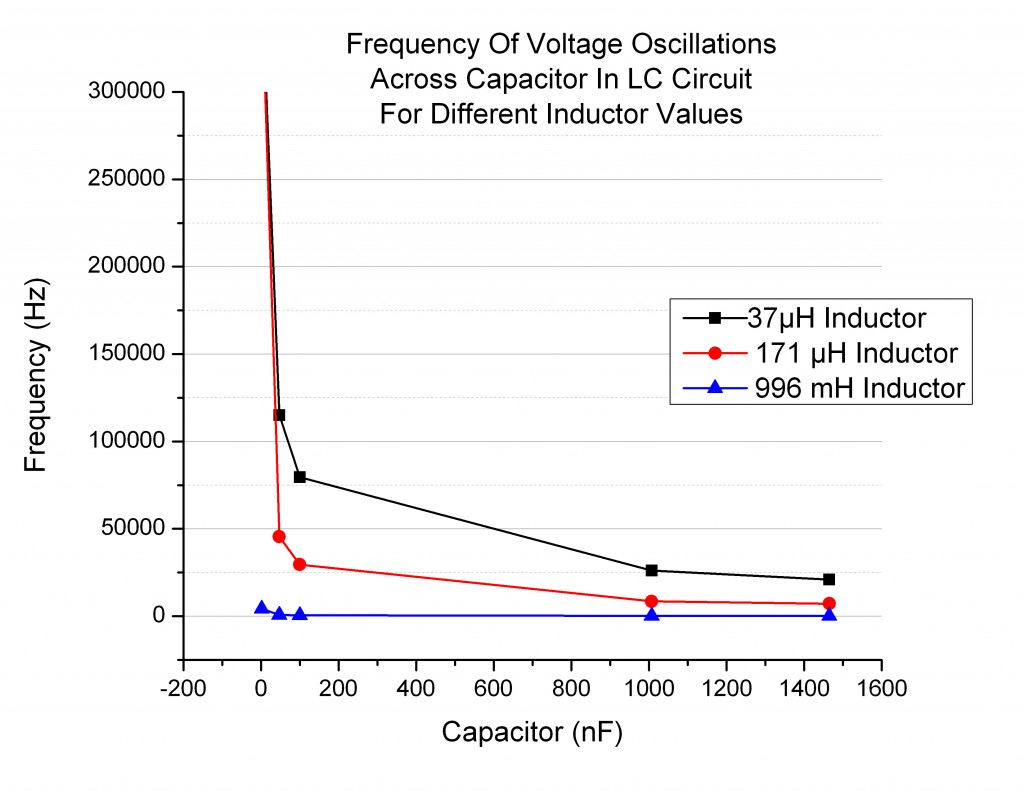
Figure 4
They reflect the predicted behavior of a 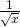 relationship, whose plot looks very similar (Figure 5). In our case the actual relationship is
relationship, whose plot looks very similar (Figure 5). In our case the actual relationship is 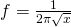 .
.
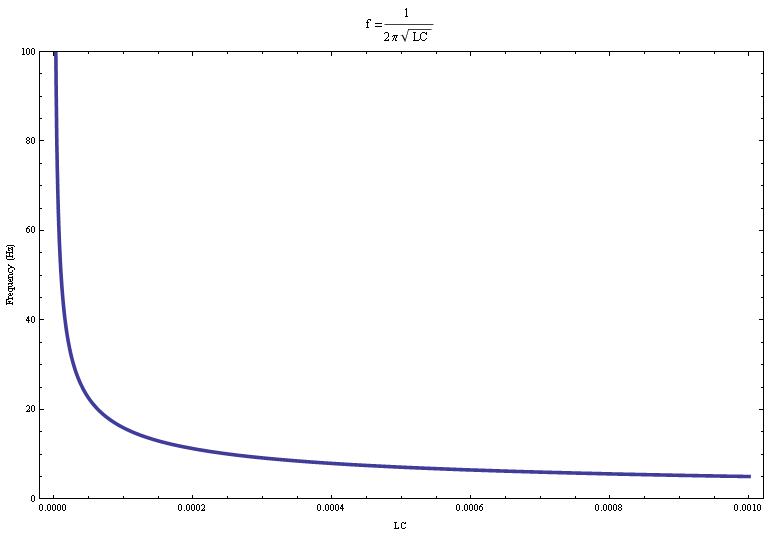
Figure 5 (Mathematica workbook: https://vspace.vassar.edu/mabjornsson/1%20over%20sqrt%20x.nb )
Exponential Decay and Circuit Resistance
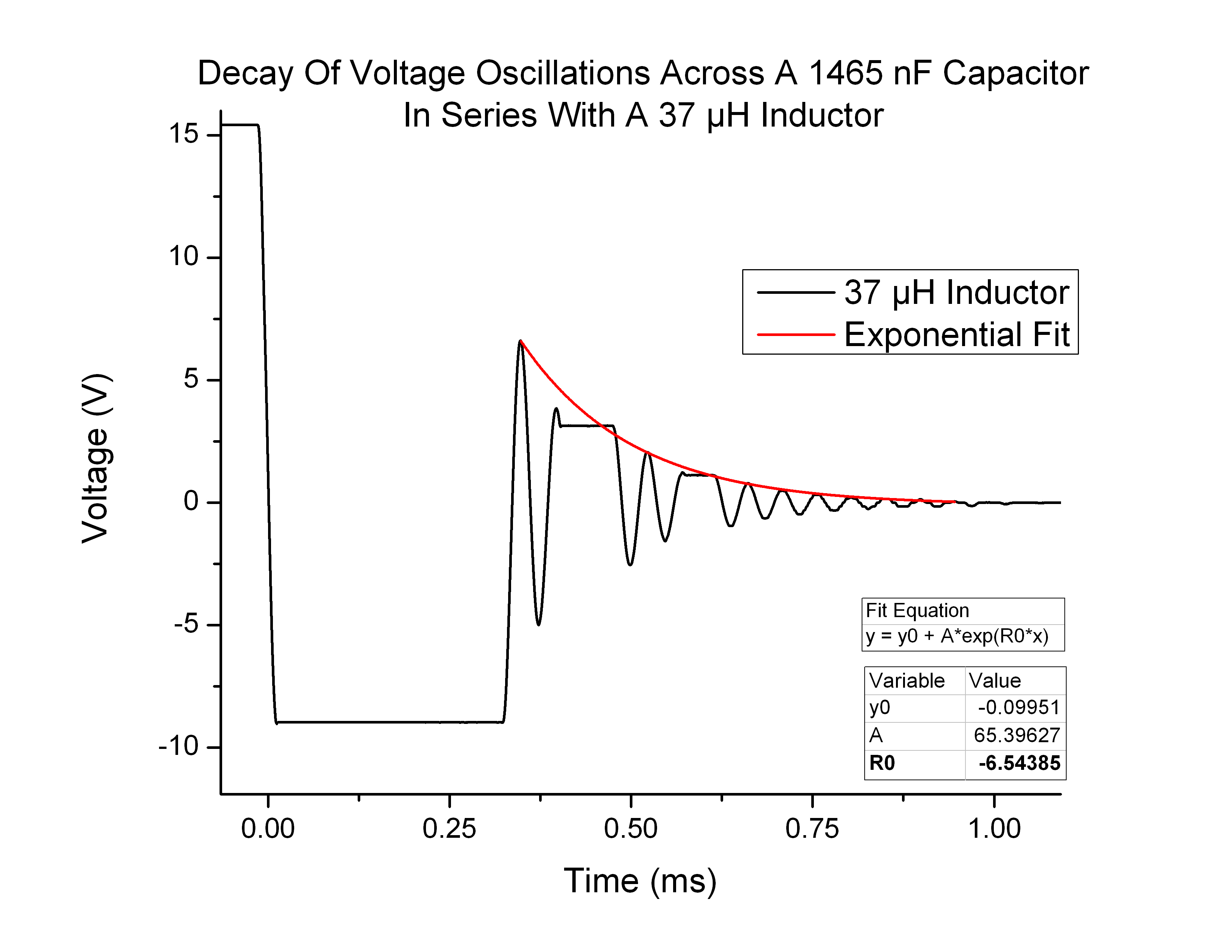
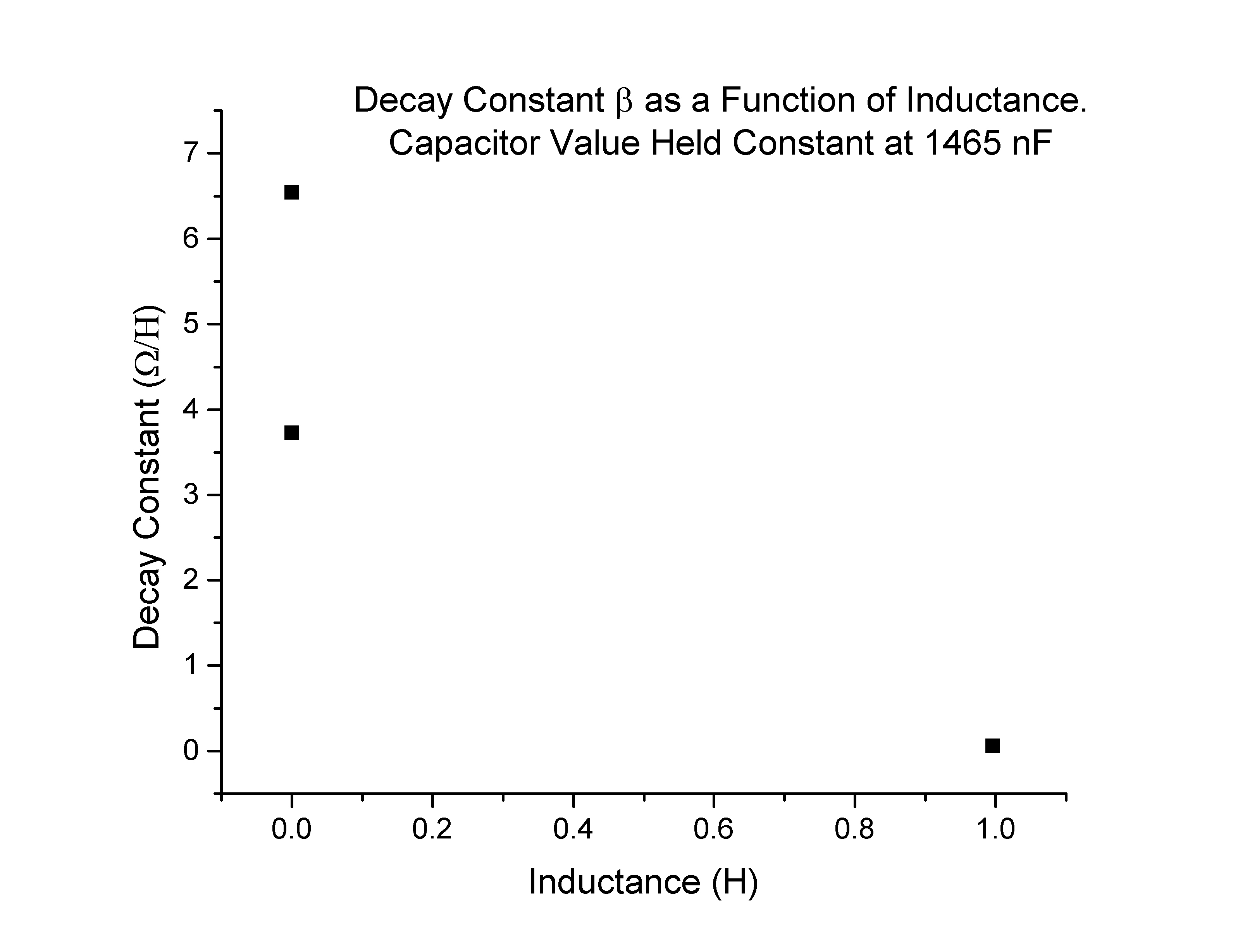
When the experimentally measured decay coefficient β is plotted as a function of inductance, the data points are sparse, and one should be cautious of drawing too many conclusions. That being said, the points I collected (Figure 6) do seem to match the expected values (Figure 7):
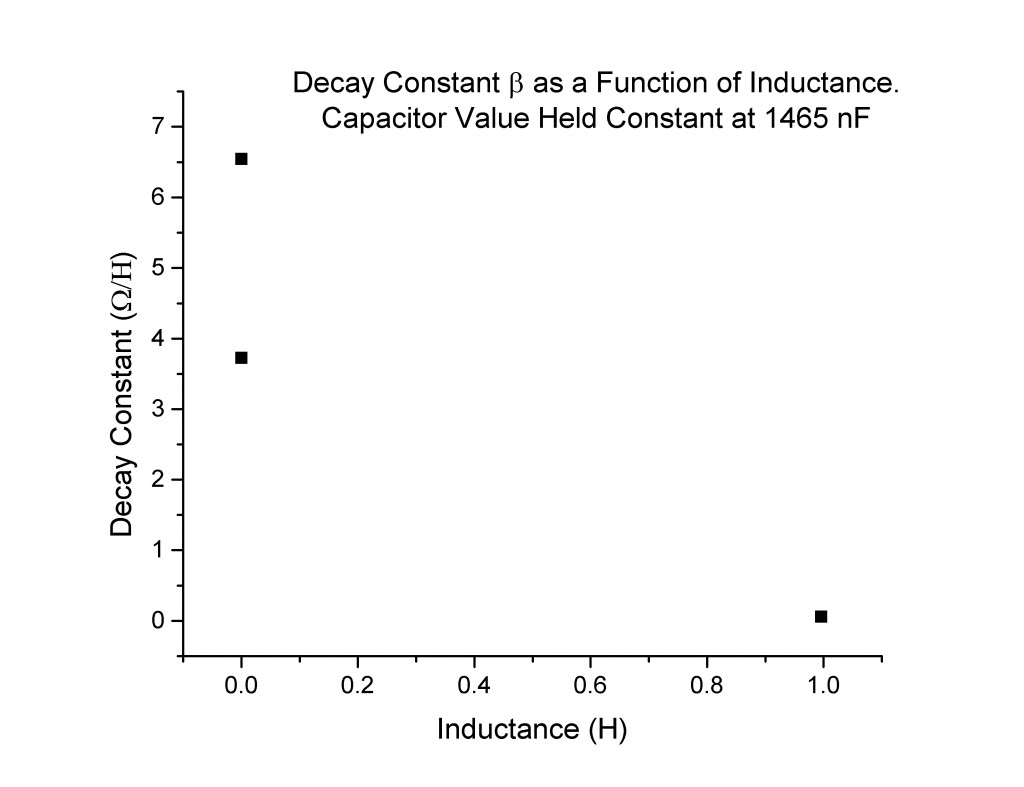
Figure 6
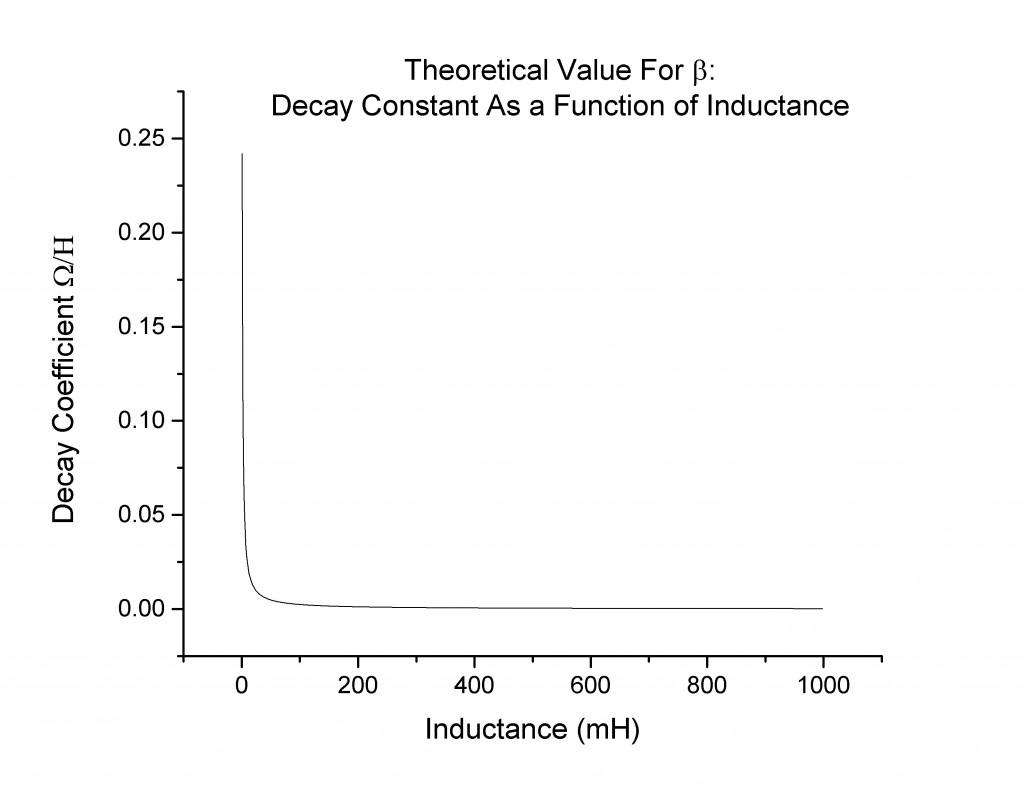
Figure 7
Finding Resistance Using β
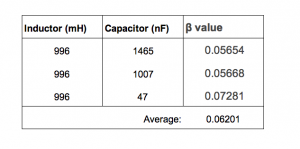
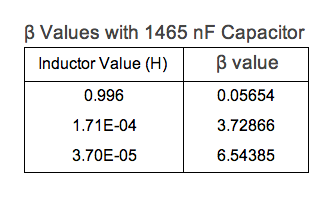
The decay coefficient β is related to L and R. Thus, since we know β and L experimentally, it should be fairly straightforward to calculate R empirically. In theory the resistance of the circuit should be the same for each measurement of β and L. Below is a table of measured values of β and L (Figure 8):
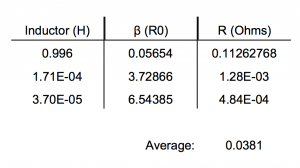
Figure 8
A value of 0.0381 Ω is a reasonable order of magnitude for a circuit with theoretically no inherent resistance. This order of magnitude is also large enough to be largely responsible for the decay of the voltage function across the capacitor.
Can Significant Conclusions Be Drawn From This Data?
With scatter plots with only three data points, the answer is “no.” To confidently confirm that my data was following anticipated trends I would need many, many more points. The most conclusive and illuminating data that I did generate wast the Voltage vs. Time graphs. These graphs were supposed to be undamped sinusoidal waves, but instead exhibited very clear damped oscillation. The collection of these curves was easy to repeat and allowed me to generate very reliable curves. These graphs confirmed that there must indeed be a significant equivalent resistance in the circuit to damp the oscillations.
Applications Of Findings
This experiment could potentially be an effective way to anticipate the inherent resistance of a circuit. My first method of using L, C, and f to find the resistance, clearly did not work, but finding the decay coefficient and from there calculating R, could very well be effective. From my limited data I got a reasonable solution, but would have to generate far more data points to confirm this resistance. It would be particularly interesting to use this method in an instructional lab if there was some way to actually measure the resistance of the circuit (maybe known values of wire resistivity, or a very sensitive meter). It would provide students with data analysis experience, such as fitting curves and using Origin Pro, as well as having hands on experience with damped harmonic systems.
Changes To Experiment
The biggest change I would make to this experiment would be to have a far greater array of capacitors and inductors at my disposal. I did not have enough to produce satisfying data. One problem I kept running into when collecting data was that one of my inductors was several orders of magnitude bigger than the others. It could have been handy to have just made my own inductors out of coils of wire. This way I would be able to change the inductance at will. Ideally I would also exchange many capacitors for one variable capacitor. It would streamline the data collection and allow for more methodical, precise data collection. I would also use components and measurement devices that could handle more than 15-20V due to the fact that such low voltage has a greater window for interference.
Sources Of Error
I have no idea how much my measuring devices and power source effect the overall resistance of the circuit. I also do not know if there are other sources of induction (albeit minor) within my circuit setup, either within components (such as the switch) or from the wires of my measurement tools coiling around themselves. There were many times when the discharge curve across the capacitor would take a strange shape that I can only attribute to some form of saturation, either the probe or capacitor. I do not know how this my have impacted my data.