Category Archives: Neo Shield

Group 5 Project Data

1 Reply

The majority of our project was done mathematically, using data collected from NASA’s logs of asteroids that came within sensor range.

The collision of any asteroid with Earth could prove catastrophic:

NEO diameter (m) larger than:
Average interval between impacts (years)
Energy released (megatons of TNT)
Crater diameter (km)
Possible effects/comparable event
– – 0.015 – Hiroshima atomic bomb detonation.
30 300 2 – Fireball, shock-wave, minor damage.
50 2000 10 ≤1 Tunguska-type explosion or small crater.
100 10,000 80 2 Largest H-bomb detonation.
200 40,000 600 4 Destruction on national scale.
500 200,000 10,000 10 Destruction on continental scale.
1000 600,000 80,000 20 Many millions dead, global effects.
5000 20 million 10 million 100 Billions dead, global climate change.
10,000 100 million 80 million 200 Extinction of human civilization.

(Table from Alan W. Harris (US) “Estimating the NEO population and impact risk: past, present and future” presented at the 1st IAA Planetary Defense Conference, 2009)

As previously mentioned, the NEOShield Project has put forth three possible solutions would handle an asteroid on a direct collision course to our planet; the kinetic impactor, nuclear blast deflection, and gravity tractors. In order to mathematically simulate the outcome of these countermeasures, we first generated two asteroids (A and B) to satisfy both extremes and allow us eventually interpolate a trend in the force needed to mitigate their flight;

Given that the average density of an asteroid is 4.95 g per cubic centimeter then:

(1)   \begin{equation*} Masteroid= 4.95 * \frac{4}{3}π^3 \end{equation*}

DIAMETER MASS REL. VELO. DIST. FROM EARTH
Asteroid A 4.1 km 1.79 E14 kg 33,100 m/s 1.89 E10 m
Asteroid B 40 m 1.66 E8 kg 6,500 m/s 1.89 E10 m

Note that the distant is constant. Also, the minimum requirement needed is to delay the asteroid by a period of 420 secs., which is the amount of time it takes Earth to move the distance of one planetary diameter, and the asteroid to pass “safely” by.

Kinetic Impactor: The weight of the Impactor is 650 kg 

Asteroid A: 

(2)   \begin{equation*} Time until Impact = \frac{distance}{velocity} = \frac{1.89E10}{33,100} = 570,997 secs. \end{equation*}

(3)   \begin{equation*} New Velocity = \frac{distance}{new impact time} = \frac{1.89E10}{571,417} = 33,075.67 \frac{m}{s} \end{equation*}

(4)   \begin{equation*} Deceleration = V1 -V2 = 33,100 - 33,075.67 = 24.33 \frac{m}{s^2} \end{equation*}

(5)   \begin{equation*} Force Needed = mass*acceleration = 1.79E14 * 24.33 = 4.36E15 N \end{equation*}

(6)   \begin{equation*} F = mΔv= m(V1-V2) \end{equation*}

(assume V2= 0 for complete inelastic collisions)

(7)   \begin{equation*} 4.36E15 = 650* V1, V1= 6.7E12 \frac{m}{s} \end{equation*}

This is faster than c, and would be improbable ! A kinetic impactor would not be used on an asteroid of this size.

Asteroid B: Using the same equations as above  with the appropriate substitutions, we are left with:

Impact Time with Delay = 2,908,112 secs.

New Velocity = 6,499 meters per second

Deceleration =  1 m/s

Force Needed = 1.66E8

V1 = 255, 385 meters per second.

This is a plausible solution in the friction-less vacuum of space, as the impactor could reach this velocity.

Nuclear Bomb Deflection:

For this mathematical simulation, we assumed that the standard B53 nuclear warhead would be employed, which has a 9 MT yield, giving off approximately 1.25E6 N of force if detonated at 30m from the asteroid.

Asteroid A:

F= ma 

1.25E16 = 1.79E14a

Solve for a = 70 meters per second squared

New Velocity = 33,030 meters per second

Initial Impact Time = 570, 997 secs. , as given by:

(8)   \begin{equation*} t = \frac{d}{r} = \frac{1.89E10}{33,100} \end{equation*}

New Impact Time = 572, 207 secs, given the delay of 1210 secs. (approx. 20 mins.)

This would slow this asteroid down at three times the magnitude needed for Earth to reach a safe position on its orbit.

Asteroid B: Using the same formulas (with the appropriate substitutions as above):

a= 75,301, 204 meters per second squared

New Velocity = 75, 294,705 m/s away from Earth, if not immediately vaporized.

This wouldn’t just slow down Asteroid B, it would send it hurtling in the exact opposite direction. Using such a method on an asteroid of this size would be the definition of overkill!

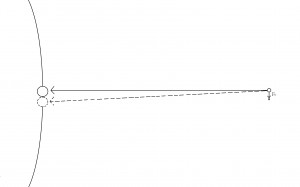
Gravity Tractor:

This method operates on deploying large “satellites” capable of sustaining and orbit around the asteroid in question and dragging it away from its original vector using gravity over a long period of time.

This operates on the equation:

(9)   \begin{equation*} F = G \frac{Mm}{r^2} \end{equation*}

Where: G is the universal gravitational constant, M is the mass of the gravity tractor(s), m is the mass of the asteroid and r is the distance the asteroid is from Earth.

Gravity Force

The diagram above depicts the path the asteroid would need to be “nudged” onto in order to safely miss Earth. At the given distance of 1.89E10 meters, it is impossible to calculate how much gravity will affect the asteroid in relation to our planet; there are too many variables, and the angle that the asteroid would need to be deflected is so infinitesimal that the mass of the gravity tractor would be unquantifiable. The gravity tractor could only be used at much greater distances over a span of decades, and even though, as a primary counter-measure to allow for easier mitigation using the kinetic impactor, or in the most serious of events, a nuclear explosion.

Visual representation:

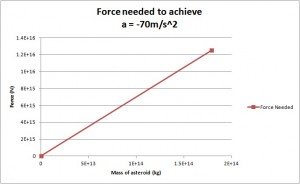
After testing these three methods mathematically, we were able to generate, as promised, a graph depicting the trend of force needed to deflect asteroids of various sizes:

Force graph

We also filmed a crude recreation of the relative process of  the kinetic impactor: (SOON TO BE UPLOADED), but the process is more expertly (though somewhat overdramatically) represented by the NEOShield PR video.

They also provide a time-table for the employment of the counter-measures.

DSCN3891

Above: Blue ball (Earth), black ball (asteroid) nail (kinetic impactor), and meter stick (measurement tool). Note that these are not necessarily to scale or proportional to one another, and that as objects moving in space are relative, that the kinetic impactor is represented as static.

DSCN3896 – depicting an uninterrupted collision with Earth

DSCN3898 – depicting the use of a kinetic impactor at nominal range

DSCN3902 – depicting the use of a kinetic impactor at a farther engagement

Data - Bomb Data for asteroid dimensions and bomb.Data - Kinetic ImpactorData for kinetic impactor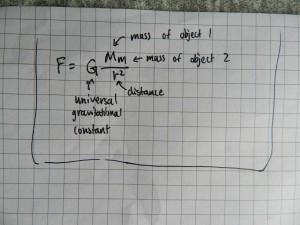Formula for Gravitational ForceFormula and theory for gravity tractor.

 

 

 

 

 

 

 

 

Group 5 Abstract

1 Reply

The scientific coalition known as the NEOShield proposes that there are three feasible methods of changing the path of any NEO ( Near Earth Objects) on a collision course with Earth: kinetic impact, blast deflection or gravity tractors. We plan to create a model of the first of these methods, and use high-speed cameras to show on a smaller scale how this  plan would work and then extrapolate using gathered data to calculate the size and speed a projectile would require to deflect an asteroid of randomly generated specifications. We will then use similar mathematics to calculate the force required from a nuclear blast to push a NEO off course and the gravity needed to pull it away, in the other two methods respectively. We hypothesize, in terms of cost and difficulty, that the kinetic impact method will be most probable.