The goal for our project was to develop an understanding of how physics methods can be used in the field of financial modeling. Primarily concerned with predicting prices and market shares over time, financial analysts have historically made liberal use of traditional physics and math techniques to best solve different sorts of systems.
A brief literature search indicated that one of the most commonly used physics tools in finance is the Monte Carlo method. Originally developed as part of the Manhattan Project to simulate the penetration of neutrons into a nucleus, the Monte Carlo method has come to refer to the general concept of using a massive amount of randomly generated numbers to simulate the development of a system based on some sort of probability distribution.
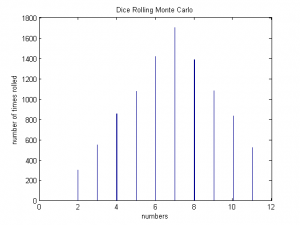
We began the project by familiarizing ourselves with basic Monte Carlo methods. First, we simulated the results of rolling two dice, simply generating two random numbers between 1 and 6 for an arbitrarily large amount of times. This basic method produced a distribution that described the most frequent combination of rolls. As expected, the mode of the distribution was 7. Next, we worked on a slightly more challenging problem, using Monte Carlo methods to numerically integrate a function. We used a rather trivial case, a circle inscribed in a unit square. The program dropped an arbitrarily large amount of points onto the system and counted how many fell within the bounds of the function. The ratio of this count to the overall number of points simulated the area of the function. The value of pi was obtained, confirming that our method was effective.
The next step was to decide which specific financial methods we would explore in depth. We decided to pursue two areas, the calculation of stock option prices and the evolution of the price of a good in a simple market over time.
A stock option is a financial tool used by traders to bet on the price of a stock over time. It allows the said trader, for a certain price, to be able to value the stock at a fixed price no matter how it changes in the overall market. A call option gives the trader the right to buy a stock at a fixed price over time, even when the market price rises significantly. Similarly, a put option gives the right to sell the stock at a fixed price over time, most useful when the stock price drops in the market over time. The problem in question is then to calculate the initial fee for which the trader can buy the right to have one of these options on the stock.
We explored three methods for pricing these options. The first was the Black Scholes method, which relies on knowing the values of several crucial parameters and the cumulative distribution that these parameters define. Equation for Black-Scholes where $C$ is the price of the option:
(1) ![]()
where
(2) ![]()
and
(3) ![]()
$N(d_1)$ is the standard normal distribution of $d_1$ and $N(d_2)$ is the standard normal distribution of $d_2$ where $d_1$ and $d_2$ are a distribution.
This method proved to be rather rigorous as it necessitated at least basic knowledge of statistical modeling and the exact value of the parameters. The second method, the Monte Carlo distribution of pricing, was more elegant. It used a uniformly distributed set of random numbers between 0 and 1 and plugged the set into an equation that needed only the original price of the stock, the interest rate, and the volatility of the stock. Finally, the most elegant method to calculate the price of an option involved the use of binomial trees. Beginning with a strike price and a theoretical return on the stock, the binomial method calculated the value of the stock at an increasingly large number of nodes in the tree and then plugged these nodes into an equation that would value the price of the option.
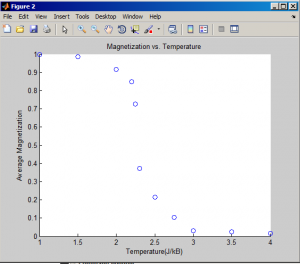
The second system we studied was based off the Ising model used to simulate the evolution of a thermodynamic system over time. The most prominent application is the simulation of a ferromagnetic material whose constituent atoms possess spin characteristics that influence their neighbors. These spins naturally tend to align themselves in the same direction, and thus we have started with a ferromagnetic system in which all spins are aligned. We then simulate stochastic changes in the system that occur because of energy added by the temperature in a heat bath. As temperature rises, the greater there is that one of the spins will orient itself in a way that requires adding energy to the system. This is because the extra heat from the increased temperature supplies extra energy. The system is solved using a Monte Carlo method to calculate the probability of each atom flipping its spin per unit time, based on the interactions with its neighbors and the overall energy. The higher the energy, the higher the probability of flipping the atom. The average spin of the system is called the “Magnetization” and is a good way to represent how magnetic the metal is.
This system is then applied to the world of finance by simulating an evolving market of agents who can either choose to buy or sell a good, which is shown by:
(4) 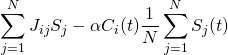
The decision to be a buyer or a seller influences the decisions of the nearest neighbors. However, all agents also are aware of a systematic trend in “magnetization” which in this case represents the price of the good in question. If there are more buyers than sellers, the price will be rising, so buyers will wish to join the sellers group to make a profit off of their good. The Monte Carlo method once again calculates the probability of these agents changing their identities, displaying the trend in price over time. The probability is given by:
(5) 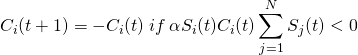
Then, the probability of an agent remaining/becoming a buyer is given by:
(6) ![]()
(7) ![]()
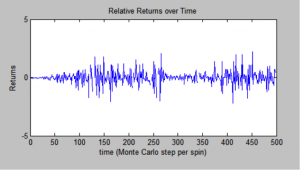
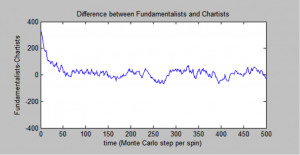
It is possible to see the stochastic nature of the pricing evolution over time, as well as the distribution of buyers and sellers in a market given some initial conditions. As we discovered, when buyers and sellers grouped with agents of their own identity, price is more volatile.
Below is a table that summarizes every method we have used, as well as providing the name of each file, found at this link https://drive.google.com/a/vassar.edu/folderview?id=0B01Mp3IqoCvhflF5azV4bHY2V0c3Vks0VXVyQkIxcnR4RmFaNDhVWEQtZGZSR2t6V2VWOHc&usp=sharing#:
| Name of Method | Purpose | Name of Code |
| “Dice Roll” | Demonstrate the efficacy of a Monte Carlo method to simulate the distribution of a large amount of dice rolls | MonteCarloDiceRoll.m |
| “Numerical Integration” | Demonstrate how a Monte Carlo method could be used to calcuate unknown parameters from an arbitrary integral | montecarloexample.m |
| “Black Scholes Method” | Uses a set of parameters with known cumulative distribution to calculate the price of an option | BlackScholes.m |
| “Monte Carlo Option Method” | Simulates the cumulative distribution from the Black Scholes method by creating a set of normally distributed random numbers that undergoes mathematical transformations | BlackScholes.m |
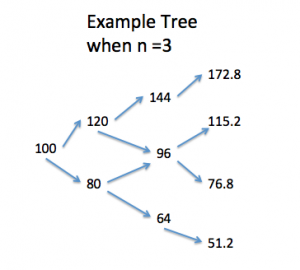
| “Binomial Trees” | Calculates the value of an option by valuing the strike price at various times based on a given interest rates. Assigns each of these values to a node in a tree and uses this structure to go back and value the option | BinomialTreesNThree.m |
| “Ferromagnetic Ising model” | Simulates the evolution of a ferromagnetic system in a heat bath by generating random numbers to calculate the probability of atoms in the system being either spin up or spin down. | IsingTest.m |
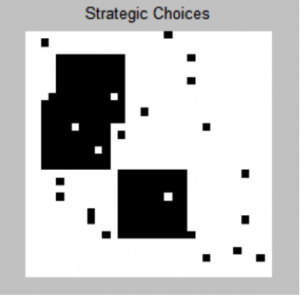
| “Market Strategy Model” | Applies the ferromagnetic ising model to a basic markets where agents that are either buyers or sellers replace the atoms. These agents follow the advice of their nearest neighbors or the tendencies of the market of a whole. These tendencies compete with each other and a Monte Carlo method simulates the probability of the agent choosing a strategy over time. The “magnetization” of this system, the average value of agents strategies, is a good way to represent the trend of the price of the good in the market. | TwoStrategyMarketModel.m |