Project Discussion
Our goal for this project was to first model a two-body orbital system such as the Earth orbiting around the Sun using the Euler-Cromer method. The second goal was to model a three-body orbital system, such as the Moon orbiting the Earth while the Earth orbits the Sun.
We were successful in modeling a two-body system, and did quite a bit of work on studying the two- and three-body orbital systems. We tried both a computational approach and a numerical method to different ends. Ultimately, we determined that although the Euler-Cromer Method works is a good way to approach a two-body system, we were unsuccessful in modeling the three-body system using the Euler-Cromer Method.
First, it must be acknowledged that mass is never involved in the computational method. Honestly, we are not sure why, and that might genuinely be the source of the problem. The analytical method we used did need the masses and the sizes, and it worked much better, which raises questions about the computational method that we employed. If we were to incorporate mass into the computational method, however, we may have run into the issue that the sun is significantly more massive than the Earth. Had we attempted to base the movement of the Moon with an equation related to mass, the Moon likely would have jumped orbit from the Earth and gone to orbit the Sun.
Secondly, we would like to bring reference frames into the discussion. We did our project in the reference frame of the sun, but what would have changed if we were approaching the project from the reference frame of the universe? Or the earth? Or even the moon? — Because we approached it from the reference frame of the sun, any effect the earth and moon’s masses had on it would not appear in the simulation. We assumed that this is an acceptable assumption, because the relative masses would make it so that the effect of these two masses would negligibly affect the sun’s motion, but we are not sure if changing the reference frame would change the results.
The conservation of energy law requires the total energy of a closed system to remain constant. In an orbital system, if energy is positive or not conserved, the orbit can turn into a hyperbolic one instead of an elliptical.
In checking the energy of the systems: we first used the equation
(1) ![]()
(2) ![]()
Which comes from combining the orbital potential energy and orbital kinetic energy:
(3) ![]()
But on second thought, $r<<R$ (where $r$ is the distance between the moon and the Earth, and $R$ is the distance between the Earth and the Sun). So we rewrote the energy of the moon as
(4) ![]()
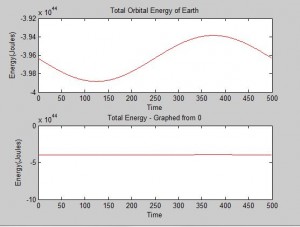
But strange “spikes” appeared in the energy plot, occurring where the radius changes dramatically. The energy plot is sinusoidal, completing one period in one orbit of the earth around the sun. We are not sure why this is so, but at second glance, the amplitude of the sine wave is very very small — it is between 4*10^44 and 4.5*10^44 Joules, so if we plot the energy from 0 the fluctuation is not visible.
Plot of Earths orbital energy for comparison:
Plot of Moon’s orbital energy:
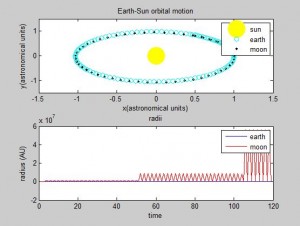
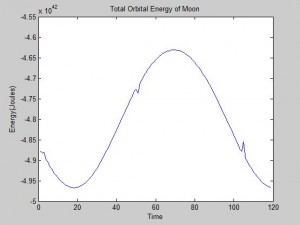
This all raises the question: is the Euler-Cromer method inherently not useful for this problem? There is a good chance the program we wrote was the reason the simulation was unsuccessful. But what other reasons could there be for the program not to work? The Euler-Cromer is an iterative method, which makes a prediction on the next location based on the most recent information. It did work well for the two body system, producing a clean simulation of the Earth orbiting the Sun, which you can see below. (The simpler Euler method is not as viable of a method because over time the calculated information would get further and further from the “true” values, because it does not use the most recent information.)
So why is analytical easier, or at least more effective, in this case? The analytical is more specific than the computational method, because the motion of the system is already known and therefore the method can be tailored for the system. We as programmers are familiar with how and why the Euler-Cromer method works, and we are confident that this method is the best for our physical system. In the same manner, we are confident that our problem lies in how we are updating the x and y position of our orbiting bodies.
Link to analytical code:
https://docs.google.com/document/d/1mKmL4spylb1h6PttlyTBY9vIuZmfnLVQhfAzvSX2qBA/edit?usp=sharing
Link to Energy codes:
https://docs.google.com/a/vassar.edu/document/d/1KzZduXpxZ6-_gEja875FwCyn0Yvc_yO69JxQJSsasvA/edit?usp=sharing
https://docs.google.com/a/vassar.edu/document/d/15wfmgWwkx_TbmMf4Untcb5DXdADvH7mSrB8Vs2DKY4Q/edit?usp=sharing

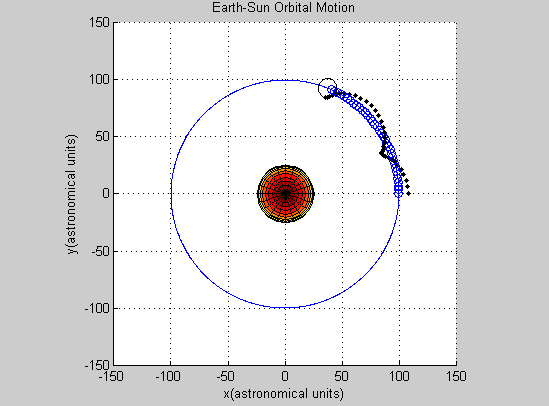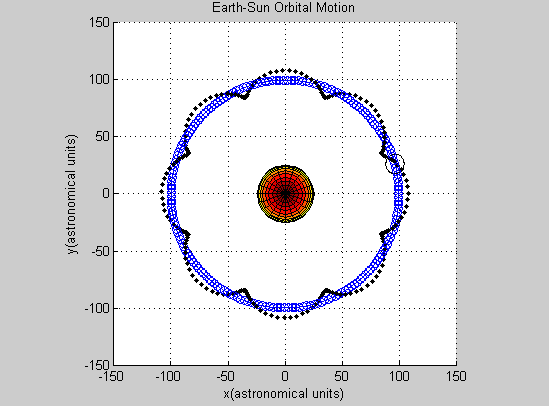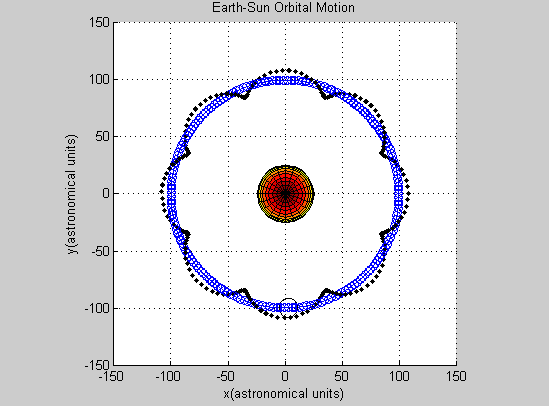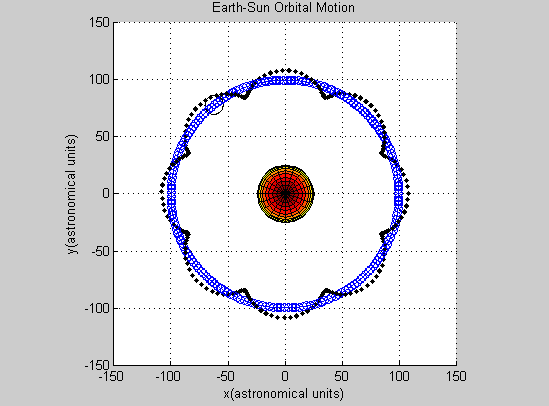

Above all, this code is very well structured and commented, so going back to find the source of a problem was not difficult. I found a few issues regarding energy that are easy fixes and give a better idea of energy conservation in an orbital system.
In both the 2- and 3-body codes, the values you have for energy are far too high (~10^11 times too high). Fortunately, this is just because AU’s were used in the final calculation of E; multiplication by a constant fixes that (1 AU = 1.496*10^11). More importantly, you were only displaying gravitational potential energy. Though this quantity should be conserved in a perfectly circular orbit, the Earth’s orbit is slightly eccentric, and even if it weren’t, a rounded value in the initial conditions (e.g. v_x for Earth at t=0) would carry through and lead to oscillating potential energy. It would be better to look at PE + KE, which should definitely be conserved regardless of eccentricity. I implemented this, and E_total turns out to oscillate only very slightly; the magnitude of these oscillations with respect to either PE or KE is on the order of time steps per year. Basically, the oscillations of the total energy is a computational artifact (we addressed this in a homework problem if I recall); what you saw in the 2-body problem was partly an artifact, but likely was primarily due to the PE you calculated, which can oscillate.
As for the spiky behavior of the moon in the 3-body problem, I suspect that this was because you may have had the updated values for xnew_M and ynew_M (i.e. with respect to the sun) depend on the position of the earth plus the previous distance of the moon from the sun, rather than the previous distance from the Earth. I tried to implement new variables that differentiated which reference frame you were referring to, but could not do this successfully. However, if you look at alternating values of the moon’s radius from Earth (i.e. ignoring the spikes), your values for r_M seem to be correct (you really have to zoom in). So, something must be happening in one step that is cancelled by the subsequent step, only to reappear in the step after that.
I also found a minor correction to r_M , which was not quite updated correctly with each loop, as r_M should equal sqrt((x_M – x)^2 + (y_M – y)^2). This reduces the size of the spikes by a factor of 100 (and they don’t keep getting bigger past a point). Another possible way to troubleshoot would be to increase the size of the plotting window (line 45) to see where the moon is jumping to for each spike (a factor of 10^6 did it for me).
However, I feel that instead of trying to fix this model, a new one entirely should be written because this one seems overly complicated to describe just three bodies (I know that this was the method in the book, hence why you used it, I just don’t think that the authors should have made it the first choice). Instead, a true N-body simulator would be best. Here, the acceleration on one body due to all the others will be calculated for each, then velocities and positions will be updated using, say the Euler-Cromer method. All bodies would be on equal footing, with no privileged bodies (e.g. a stationary sun with no direct gravitational effect on the moon). Best of all, there will be no reference frame issues (though you would want to be sure that the initial net momentum is 0 so that your system doesn’t drift out of view).
Overall, the well structured and commented code made this an enjoyable project to evaluate; I only had trouble with the model, and all problems were traceable, though still not always easy to address. This is important, as I have dealt with code that was harder to decipher before, and half the work in those cases was just understanding the layout! Here that was not an issue.
Good job thinking about where the problems in your project lie. At this point it would be really important to figure out if the problem is with the computational method or with the programmer.