As we began our project, we realized that the Ising model presented in Chapter 8 of Giordano and Nakanishi quickly introduces many aspects that are not relevant to our neural network model, namely the idea of a heat bath at temperature T. Our neural network is essentially an Ising model assumed to have a temperature of 0, so much of Chapter 8 is unnecessary for our model. So we skipped ahead and went straight to simple neural networks, as described in Section 12.3 of the text.
The essential elements of our model are an NxN stored pattern, an interaction matrix Ji,j of size N2x N2, and an input pattern of size NxN. After a pattern is stored (by creating the network’s interaction matrix), an input pattern (usually one similar, but not identical, to the stored pattern) is presented. This pattern is then changed according to the Monte Carlo method, and, if things worked correctly, the output is the same as the stored pattern.
Stored Pattern:
We created a stored pattern on MATLAB by creating a matrix +1’s and -1’s. Our first pattern is the letter ‘A’, following the examples in Section 12.3 of Giordano and Nakanishi, on a 10×10 matrix. As mentioned in our earlier posts, each element in the matrix represents a neuron and if the neuron is active it has a value of 1 and if it is inactive, its value is -1. Our ‘A’ pattern is made up of +/-1s where the +1’s represent the pattern and the -1’s represent the background. When these numbers are displayed in the command window, the A pattern is not easy to see, so we use the imagesc command (along with an inverted gray colormap) to better visualize our patterns.
Element Indexing
MATLAB indexes the elements in a matrix with two numbers: the first index refers to the row of the matrix, and the second index refers to the column. For our neural networks, we want to be able to access every element in the array (twice, separately) in order to have every neuron interact with every other neuron. The easiest way to do this is by using a single number index, i, which runs from 1 to N2. In our code, we use i and j. To actually access the elements in our matrices, we have to use the normal double MATLAB indices, which we call call y and x. The index i can be calculated from the normal y and x indices using equation 12.20 from the text.
![]()
In our code, we frequently have two sets of nested for loops, with which we are able to loop through the entire pattern twice, once with the index i and once with the index j. For this reason, we use the indices y_i,x_i and y_j,x_j.
Interaction Energies J(i,j):
The interaction energy matrix describes the interaction between every neuron with every other neuron. So if we start off with a P_stored matrix of size NxN, then the J matrix for it is going to be size N2x N2. In order to determine the values for the J matrix we need to use equation 12.16 from the text,
where si is the value of neuron i in pattern m, and sj is the value of neuron j in pattern m. Thus, the J(i,j) matrix is created by multiplying the values of P_stored(y_i,x_i) with the values of P_stored(y_j,x_j). In order to do this on MATLAB we created two for loops where we held the y(rows) values constant and varied our x (columns) values. By doing this we compare P_stored(1,1) to P_stored(1,2), P_stored(1,3), P_stored(1,4)… Then after finishing with the first row the program goes on to compare P_stored(1,1) with P_stored(2,1), P_stored(2,2)… This continues until P_stored(1,1) is compared with all the other points in the matrix and then it does the same thing for P_stored(1,2), P_stored(1,3), and so on.
Example 1:
Below you will see a P_stored matrix and it’s corresponding J matrix. By using equation 12.20 and the double for loop, you are able to index the values for i and j which allows you to create J(i,j).
The interaction energy matrix values will later be used to help determine the amount of energy it takes to activate or inactivate a neuron.
Neural Network Model
After finding our interaction energies, we now have an operational memory for our simple neural network. In order for our neural network to be operational we need to create a pattern within P_stored. In order to do this we created an image of the letter A by manually entering in the 1s to create the letter A. We then created a new matrix called P_in to represent the matrix that we will sweep using the Monte Carlo method. P_in is created by randomly flipping the value of some of the neurons in order to distort our original A pattern. In order to make it easier to visualize, we used the function imagesc to turn our matrix values into an image.
After conducting a Monte Carlo sweep over our distorted A-pattern P_in we should get in return the same pattern as our P_stored matrix. Thus, our neural network remembers being fed the desired pattern we stored earlier. In the figures below, the black squares are represented by +1’s in our matrix and the white squares represent the -1’s.
Monte Carlo Method
The method by which the input pattern is changed into the output pattern is the Monte Carlo method. The essence of this method is to calculate, for each neuron in the input pattern, the effective energy of the entire neural network in its current state using Equation 12.14.
If the total energy of the network with respect to the neuron i is greater than 0, then neuron i’s value is flipped (+1 -> -1, or vice versa). If the total energy of the neural network with respect to neuron i is less than 0, its value is unchanged.
This process is carried out for every neuron i, so that every neuron is given a chance to flip. Once every neuron has been checked, one sweep of the Monte Carlo method is complete.
For our current code, we are only using one Monte Carlo sweep, but as we progress forward we will use multiple Monte Carlo sweeps to check if the output pattern is stable, and to see if multiple steps are needed in order to fully recall the stored pattern.
Our full script that includes all the parts discussed above, is attached below.
Brian and Tewa Initial Code for Neural Networks Project
Future Plans
Next, we will begin to characterize the properties of our model. We will be investigating questions how different P_in is from the stored pattern, the maximum number of patterns that can be stored in a network, and how long pattern recall can take. The work for this post was done exclusively together as a team, and moving forward we will begin to split up a bit more as we tackle independent questions. As we do this, we will be splitting up our code into smaller chunks, some of which will be re-defined as functions, for easier interaction.


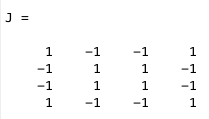
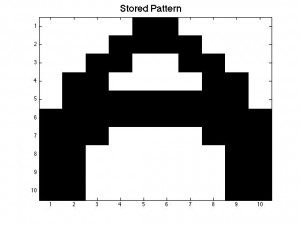
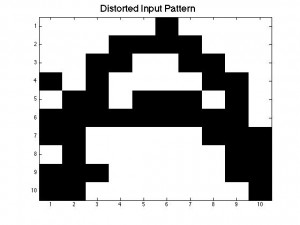 Figure 4
Figure 4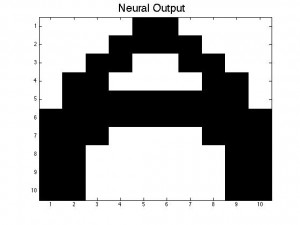
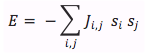

Good job explaining the N^2 x N^2 matrix. I have a lot of questions about this interdisciplinary project. Are you borrowing the physics from statistical mechanics? Could you give some background? What is your definition of a neural network in this context? What is your goal in this project? Is it related to pattern recognition? Is the energy of the system assumed constant? A flow diagram for your program would be really great! Good job in commenting on your code! Could you explain your Monte Carlo method in more detail? How does that algorithm work?