Last week we used Matlab to record original audio file using a desktop computer microphone.
Please find the code here:
https://drive.google.com/a/vassar.edu/file/d/0B4quZV7NVNf7MFFWU0lMVGpEZ00/view?usp=sharing
Upon contacting the appropriate members of the Vassar physics faculty, it has come to our attention that the school does not posses an ultrasound detector. We then tried extremely high sampling rate using a normal microphone to try and capture ultrasound frequencies with no avail.
instead we took a signal with a frequencies in the infrasound range, even though it was not originally a sound vibration. specifically we took the power signal from a red and green laser inside an interferometer from the Fourier transform spectroscopy lab and turned it into a wav file. We then took the fft of that wave, and used the circshift function on the fft data to moved it up in the frequency spectrum to the audible range.
Please find the code and necessary audio file here:
https://drive.google.com/open?id=0B4quZV7NVNf7LXJqNERTZEpYckU&authuser=0
https://drive.google.com/open?id=0B4quZV7NVNf7VW5LTVczUUNablVBMzkzdmJWOWctclRxSGdZ&authuser=0
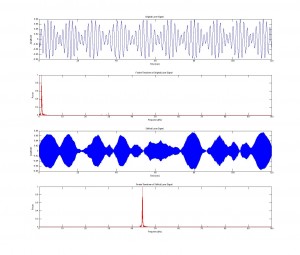
Notice the shape of the shifted signal. We hope to account for the error in the audible signal by accounting for the harmonic ratios.
This method of frequency shifting does not change the amount of time the file takes up, but it does not maintain the ratio between the frequencies. Because the shift is linear, it changes the harmonic interval between the frequencies. An example of this would be an interval of an octave. if you have a frequency of 200 Hz the next octave of the same musical pitch would be twice the frequency 400 Hz. If you shift both of those frequencies up linearly by 100 Hz you would have frequencies of 300 Hz and 500 Hz. The ratio between the two new frequencies is different than in the original. The effect is made noticeable in the following examples:
Shifting up 34 Hz
Shifting Up 39 Hz
Shifting Up 44 Hz
The next step is to maintain the harmonies using a by keeping the ratios constant as we shift the frequencies. Matlab’s findpeaks function will aid us in performing this task.
We decided to make a signal of our own and play with changing frequencies to see how it effects the wave and its Fourier transform.
Please find the code here:
https://drive.google.com/open?id=0B4quZV7NVNf7SEZqeEtTY2dRU2s&authuser=0

