Before I comment, let me apologize for getting this done somewhat late. I’m at a conference in Pittsburgh right now and it’s been crazy!

To begin, I found the goals of the project to be quite clear: to perform frequency shifting on recorded or computed sound signals, specifically ultrasound signals. I’ve personally often wondered about this problem, and the ramifications of trying to fix it (i.e. with respect to a record player which, when spinning at the wrong frequency, either plays back sound too low and slow, or too high and quickly).

Next I move to your “Ultrasonic Analysis” post.

Your explanation of “ultrasonic” is crystal clear, though I suppose the name is pretty straightforward. Next, however, you mention that it is necessary to sample at a rate slightly higher than the Nyquist frequency—why is that? I suppose it’s because you have ultrasonic (above 20000 Hz) signals, but when I first looked through this that fact wasn’t immediately clear. Also, what was, all in all, your higher frequency bound (at least at the outset, before you realized you couldn’t measure ultrasonic sound)?

So you’ve changed from shifting high frequencies down to shifting low frequencies up, since you couldn’t detect ultrasound. Are there any major differences, that you know of, in the two approaches? Is one more difficult than the other? It seems like you have to worry less about aliasing errors in the low frequencies, which is nice. Also, the frequency difference between octaves (or other harmonically “nice” steps) is much smaller than an high frequencies. Does this mean that techniques that preserve harmonic qualities are easier to implement?

Now I’ll discuss your “Preliminary Data” post

The inclusion of several examples is quite well done here. With respect to audio, it’s not too cluttered, but gives enough context for those who may be unfamiliar with the basic concepts. However, I do think some visual examples could be beneficial. I think that a combination of sight and sound can really make what you’re doing clear to the reader/listener.

You’ve explained up- and down-sampling really well—I’m just curious how the algorithm is put into practice. Did you experiment with removing different points, and compare the results? Would there even be a noticeable difference?

I’m a little confused when you talk about phase shifting… is this just shifting in the frequency domain? I was always under the impression that “phase” had a different meaning for acoustic waves, which is extracted from the imaginary sound data in the frequency domain.

Now I’m discussing your “More Results” post.

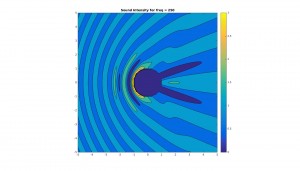
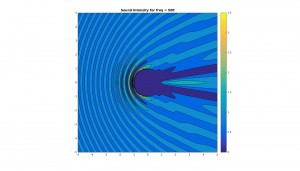
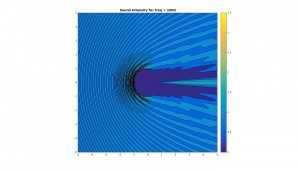
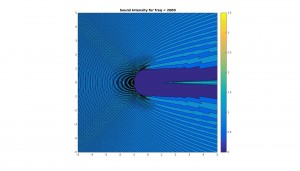
About halfway down, you mention the “harmonic quality” situation—this would be the perfect place for an image (perhaps show it logarithmically so that you don’t bunch up the high frequencies in the graph), to help those of us who prefer to learn visually. Or, perhaps a better way would be to come up with a pretty universally understandable analogy that makes the comparison/conceptualization easier for the viewer. I’m not sure what this would be, but maybe you could think of something.

I like that you again included several sound files, since it gives listeners that perhaps couldn’t perceive differences during your presentation another chance to go back and listen for some subtle differences, especially with regards to harmonics characteristics (or if anyone decided to listen before your presentation).

Now I’ve moved to your “conclusions” post

Again you’ve shifted—back to high frequencies. Why is this?

Conceptually, your methodology makes a lot of sense to me; it’s pretty straightforward to imagine what’s going on. However, I’m still a little confused as to the actual algorithm you used. Did you use the downsampling technique you meantioned earlier? It looks like, from your graphs, that you performed a “circshift” in the frequency domain.

You say “rat mediation”… I wonder, did you mean “rat meditation?” Silly rats.

What you mention right before your future work—making an abrasive sound from two sinusoids—is super cool. I’d love to see some results there. Future work sounds cool—so, say you were to mulitply your signal by 2 in the frequency domain. Is that what you mean by “transposition?” Were there any big problems that made it difficult to do this analysis? I imagine that a little more than just multiplying by a constant goes into it.

Other remarks:

I also wanted to mention that during your talk, you mentioned the “harmonic relations” between frequencies, and how such relations (since they are ratios) are not conserved. You explained that this could lead to dissonance and other sort of unpleasant sounds, which I think you demonstrated superbly both with your description and with your audio example. Well done.

Overall, this project was very interesting, and relatively easy to follow conceptually. I appreciate the focus on sound and demontrating sound behavior to the audience. As I mentioned periodically, I think your work could benefit from some more visuals (that is not to say that the images you do have are not good; I think they are actually quite appropriate).

I’ve endeavored to model the scattering of an acoustical plane wave off of the surface of a rigid sphere. As with most computational models, we have no “reference” with which to compare the results–how can we know they’re accurate? And even though analytical solutions exist for the problem, they are (1) not perfectly implementable since they require infinite sums (which must be truncated) and (2) they are quite challenging to program, and we have no intuition for how they should look. An analysis of limiting cases and of the actual physical scenario are therefore needed to determine whether or not the results are accurate.

With regards to point (1) above, in order to practically solve the problem at hand we must truncate an infinite sum. So how do we know where to truncate? One possible method involves the addition of more and more components until the solution stops changing noticeably (for this project results are plotted and changes found by inspection), or actually begins getting worse (for more on this see my most recent post on pages.vassar.edu, specifically where aliasing errors are discussed). Keeping only the first sqrt(M) terms in the sum, where M is the number of points on the sphere for which the scattering was computed (or the number of sampling points), was found to be sufficient. This number was also found in the literature cited for this project.

For point (2), the examination of limiting cases is crucial. First, however, let’s consider what variables we’re dealing with. The primary independent variables of our scattering problem are sphere radius and sound frequency. If one imagines the relative sizes of the wavelength, though, which is essentially interchangeable with frequency, and the sphere radius, it becomes clear that there is really only one independent variable: the ratio of wavelength to sphere radius. In other words, increasing the sphere radius is the same as decreasing the wavelength of incident sound, and vice versa; the physical scenario remains essentially the same.

We therefore focus on the effect of frequency on the scattering pattern. For very low frequencies, when the wavelength is much bigger than the size of the sphere, we should expect very little scattering, since such a huge wavelength effectively “ignores” the sphere. What scattering does occur should be relatively uniform, since the sound field varies little with respect to the size of the sphere. For high frequencies, when the wavelength is much smaller than the radius of the sphere, we expect the sphere to act like a “wall” and reflect a good portion of the sound back towards the angle of incidence. For wavelengths comparable to the radius of the sphere, the results become quite interesting. We expect some sort of complex scattering pattern that is neither uniform nor immediately predictable, though we still expect the majority of the energy to be scattered in the direction of incidence.

With a look at the figure below, which shows cross-sectional scattering patterns for 200, 300, 341, 400, 600, 1000, 2000, and 4000 Hz, respetively, it is clear that these expectations are met. I think we can rest assured that these results are accurate. Note that 341 Hz corresponds to a ratio of exactly 1 between the wavelength and radius of the sphere, as the radius of the sphere was chosen to be 1 m and the speed of sound 341 m/s.

For sake of space and visualization, each graph has been normalized. In practice, the low frequencies scatter very little energy in comparison with the higher frequencies. Note how uniform the lower frequencies are, and how the higher frequencies approach a delta function in the direction of incident sound, just as expected. 600 Hz looks especially interesting; I would never have guessed such behavior at the beginning of this project.

Finally, why do we care about this work? One of the main reasons is that it provides the basis for measurements of sound energy using a spherical microphone (a rigid sphere with many microphones on it). In order to measure the sound on the sphere, we need to know how sound behaves on the sphere. A spherical microphone, using a technique called beamforming, allows us to extract directional information from a sound field (i.e. to determine from which angle the majority of sound energy is coming). This is the what I’ve attempted to do in my thesis. In addition, a spherical microphone also allows one to “reconstruct” a sound field (think virtual reality or sound maps) whereas a normal microphone does not. Future work for this project could include developing beamforming techniques, creating a system that can “intelligently” determine direction of incoming sound, and extending the scattering analysis to other shapes of interest, perhaps a hemisphere or 3D polygon of some sort.

The previous presentation of results was very limited–limited in the scope of the actual results that were presented, and limited in the scope of analysis. Here, I present further results with a greater analysis of implications, limitations, etc.

First, let us consider why we care about such a scenario. A sphere is a relatively simple object, but also a very interesting one. Many other objects can be modeled as spheres, or as a combination of several. For me personally, I have been working with a spherical microphone, and since I wish to understand how the sound behaves on the surface of this microphone, I need to take into account how the sound is scattering from the microphone. This is the main practical application I am familiar with, though there are bound to be others.

An acoustic plane wave is very simple and is best shown with an image rather than an equation. Note it is very much like it sounds (no pun intended): a plane (in the mathematical sense) traversing through the air.

Source: commons.wikimedia.org

Now, to understand how this plane wave interacts with a sphere, we need several things: 1) for convenience and simplicity, a way of describing the plane wave using spherical coordinates; 2) a series of functions known as spherical harmonics; 3) and to meet a couple of boundary conditions called the Dirichlet Boundary Condition and the Sommerfeld Radiation Condition.

I won’t go into detail here about 1) and 3), but shall simply show results below. As for spherical harmonics, they are to 3 dimensions what Fourier Series are to 2 dimensions: they allow us to break apart 3D shapes or fields into an infinite series of functions. For more on spherical harmonics, see the end of this post.

The equation describing the pressure field at the surface of a rigid sphere (after being struck by plane wave) is as follows:

Where i is the complex unit, n is a term representing the sum index as well as the spherical harmonic order within the sum, k is the wave-number of the acoustic plane wave, a is the radius of the rigid sphere, m is the degree of the spherical harmonic, Θ_k is simply the (theta, phi) pair representing the direction of incoming sound, Θ_s are the (theta, phi) pairs of every point at which we’ve chosen to evaluate the pressure field (or the “sampling points”), and Ynm is the spherical harmonic of order n and degree m. Finally, bn(ka) is given by:

where jn and hn are the type one spherical Bessel and Hankel functions, respectively, and the apostrophe (‘) denotes their derivatives. Note that this pressure field is the very solution we want–that is, the equation of very near field scattering and diffraction all in one. In fact, it is actually a superposition of incident energy and reflected energy (for more on this, see reference [1] below.

Now, in principle this first equation is exact; it yields perfect solutions with no errors. In practice, however, we must approximate this solution on several levels:

1. We must truncate the sum in the first equation, as finite computing power only allows finite calculation of spherical harmonics and bn,
2. The Spherical harmonics, spherical Bessel and Hankel functions (jn and hn) must be approximated, as they do not have a simple analytical form,
3. The number of points at which we can evaluate the pressure field on the surface of the sphere must be finite (e.g. would could choose 64 evenly spaces points, or 128, etc.); ideally we could choose infinite points

Our main priority here are bullet points 1. and 3. Matlab does a very good job of approximating the Spherical Bessel and Hankel functions, and the error attributable to them is small in comparison with the other two errors. Let’s discuss points 1. and 3. in detail (they shall be discussed together since they are related):

Let N be the maximum spherical harmonic order, or the maximum order of our sum (replacing the infinity in equation 1).

For small N, there are huge errors in the calculated sound field because the spherical harmonics fail to truly estimate the shape of the sound field. They simply can’t produce the detail fine enough. Let’s illustrate the point graphically. Below are the cross-sectional graphs for N=0, 1, 2, and 10 for the sound pressure field at the surface of the sphere, for a plane wave of frequency 1000 Hz.

Notice how the first few graphs fail entirely to capture the true detail of the sound field, whereas the final graph is quite detailed. Spatial errors of this sort, due to the truncation of the sum of spherical harmonics, are called spatial Aliasing Errors.

Another type of spatial aliasing occurs when we try to examine high frequency sound. Since we only have a finite number of points to work with, higher frequency sound tends (or shorter wavelength) to be harder to model. The reason is this: as the wavelength gets shorter, it begins to approach the distance between our samples (if we’ve chosen 64 evenly spaced points, for example, there is finite distance between each point). Once this happens, we no longer have enough samples to reconstruct the sound field. This behaviour is akin to the Nyquist Frequency and sampling rate: signals with a frequency higher than the Nyquist Frequency simply can’t be reconstructed accurately. Let’s look at this graphically as well. Below are the cross-sectional graphs for N=10, 20, 30, and 100 for the sound pressure field at the surface of the sphere, for a plane wave of frequency 20000 Hz. 128 Sample points have been used.

It’s looking good, it’s looking good… and it fails. We’ve maxed out our capability to model the sound at 20000 Hz, and further addition of spherical harmonics, after a certain point, actually gives us worse results.

So, it was seen in practice that choosing a maximum order of approximately N = sqrt(M)-1, where M is the number of sampling points, was ideal for most cases. Addition of higher orders may lead to frequency related spatial aliasing as shown above, though in practice it has been observed that somewhat higher values of N may (a few orders more) may also be acceptable [3].

Below are graphs for the 2D cross sectional area of the sound pressure at the sphere, and the corresponding sound field around the sphere. Results are shown for octave bands between 100 and 8000 Hz (125, 250, 500,1000, 2000, 4000, 8000), the frequency range most important for human hearing. Number of sampling points and N have been adjusted periodically to improve resolution.

Sound field on sphere:

Contour plot of sound field in vicinity of sphere (x and y axes are simply xy-coordinates in meters):

Notice how, for low frequency (long wavelength) the scattering is actually quite low. This should make a lot of sense physically, since the larger the wavelength with respect to the sphere, the more likely the sound is to simply diffract around the sphere and “ignore” it altogether. On the other hand, for higher frequency (shorter wavelength), the scattering becomes quite large, especially at the front of the sphere. This should also make sense, because the spherical boundary becomes more and more like a flat surface to a smaller and smaller wavelength, and hence reflects sound approximately back in the incident direction. Note too that for high frequency there much less diffraction than for low frequency.

TODO: more in depth analysis of error, especially numerically. Clean up code. Comparison to limiting case of Rayleigh scattering.

—————————————————————————————

NOTE: Here is a table describing the function of the code. Below the table is a link to the updated code, which have vastly improved commenting to facilitate use. I would recommend using rigid_sphere_scat_2D over its 3D counterpart, simply because the 2D is so much easier to visualize, and since the scattering is symmetric, it tells essentially the same info.

Link to code:

https://drive.google.com/a/vassar.edu/folderview?id=0B3UNwnkM9fLrfkRlb05LdEVOTzhCQWRuRHRCVVFjUDJIMHBpWlF2V3ZKd3UwWXNwVWRua28&usp=sharing

Spherical Harmonics [2]:

Note that spherical harmonic order starts at 0, not 1.

References:

[1] http://ansol.us/Products/Coustyx/Validation/MultiDomain/Scattering/PlaneWave/HardSphere/Downloads/dataset_description.pdf

[2] http://mathworld.wolfram.com/SphericalHarmonic.html

[3] O’Donovan et al. Imaging concert hall acoustics using visual and audio cameras.

[4] Li et al. “Fast time-domain spherical microphone array beamforming.” IEEE Workshop on Applications of Signal Processing to Audio and Acoustics. 2007

Using MATLAB, I’ve created several functions to visualize scattering from a rigid sphere. I’ve included three pictures below, as well as the MATLAB code (Note, code is still in rough form. Commenting and overall readability shall be improved). In all Images, the sound is incident from the left. In the next post, I’ll go into more detail with regard to the actual mathematics; during the past week my greatest priority has been to simply get the code running. For now, here’s the equation describing the sound field due to plane wave scattering from the rigid sphere:

where jn and hn are the Spherical Bessel and Hankel functions of the first kind, respectively, Pn are the associated Legendre Polynomials, x is simply the x coordinate, k is the wave number, and i is the imaginary unit. Notice that since we have an infinite sum, in practice we must truncate and approximate this solution.

The first–a two dimensional cross section of the pressure incident on the sphere from a plane wave (frequency of ~54 Hz). The red curve is simply for visualization of the sphere; it has no other significance in this plot. Note how the greatest pressure is on the face of the sphere, and the least is on the sides and around on the directly opposite side.

Next is the same graph, but extended to 3D. Note the similar shape, but a little more pronounced as this is for 100 Hz and the previous was for ~54 Hz.

Finally, the intensity of the sound field; this includes both incident and scattered sound energy, and one can therefore see the constructive and destructive interference patterns. This is for a plane wave of ~54 Hz.

CODE (note I’ve removed large comments from the front of the code for the purposes of space)

Note: all code to run these simulations should be present. If you can’t get the code to run, please let me know.

Here is a link to the code in Google Drive:

https://drive.google.com/a/vassar.edu/folderview?id=0B3UNwnkM9fLrfjNyTDJEc0tQeklHTTBueFEtMDRZMUVJWnpvV2p4MFpLbHlpVTJ4QXJCXzg&usp=sharing

An acoustic plane wave is defined much as you’d expect: as a “plane” of sound energy traversing a medium. When this wave encounters an object, there are several possibile outcomes:

1) Diffraction–the sound is “bent” around the object and its path is therefore altered;
2) Scattering–the sound is reflected off of the object and its path is thus altered;
3) Refraction–the sound passes through the object and its path is therefore altered due to a change in medium.

In this project I shall consider only diffraction and scattering, as the “object” I have chosen is a perfectly rigid, acoustically non-transparent sphere (i.e. sound cannot pass through it). In practice, it is seen that diffraction occurs for high wavelength (low frequency) sound only, and as frequency increases, scattering becomes the dominant phenomenon.

Like any wave, there is a wave equation dictating the propagation of an acoustic wave. Its solution is, however, quite complicated (especially in the presence of objects/barriers), and although analytical solutions exist for diffraction and scattering on a sphere, its components, which require complex functions such as Spherical Bessel and Hankel functions and their derivatives, whose values cannot be precisely (analytically) determined using computational methods, and which therefore must be approximated much like we approximated the solutions to differential equations using the Euler, Runge-Kutta, or similar methods.

For the sake of illustration the acoustic wave equation in three dimensions is:

Notice that this is a 2nd order differential equation the likes of which we have handled in class.

The layout of the project is this (in order of importance):
1) to use the acoustic wave equation to numerically solve the problem of diffraction (low frequencies) and scattering (high frequencies) of the wave on the surface of a rigid sphere;
2) to compare this result to the analytical results available;
3) to provide a visual or graphical representation of the phenomena;
4) to discuss error propagation in numerical method and the method by which the Spherical Bessel and Hankel functions described earlier are approximated;
5) to, if possible, discuss the spherical harmonic decomposition of sound on the surface of the sphere, which provides a rigorous basis for accurately modeling the sound up to a certain frequency.

This last point also requires the evaluation of integrals (in a way analogous to that of Fourier Transforms in 2D), which by the nature of computation are impossible to solve perfectly using numerical methods, but must be approximated as sums. If I am able to include this last point, I will also discuss the method of approximating the integrals.

An acoustical plane wave, much like a light source, displays diffraction patterns based on the object it encounters (slits, shapes, objects, etc.). A sphere is one such object of particular interest, as the diffraction pattern produced by a sphere can be used to deconstruct sound signals on the surface of the sphere (a signal which would otherwise be nonsense because of the diffraction). Spheres have been increasingly used in recent years as the basic geometry of microphone arrays, and they offer many advantages over, for example, linear microphone arrays. The project will therefore focus on modelling and visually displaying diffraction of an acoustic wave due to a sphere, and will (hopefully) delve into spherical harmonic decomposition of the sound field on the sphere.