Author Archives: anrivera

Precession of Mercury: Conclusions

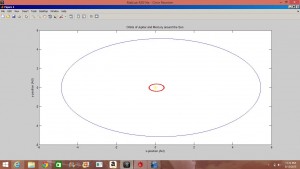
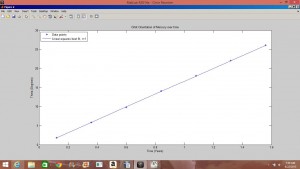
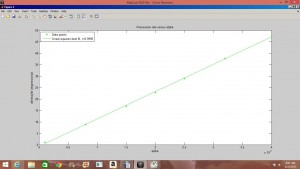
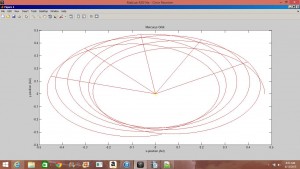
The precession of Mercury is caused by the gravitational effects of the other planets (Jupiter contributing the most) and the general relativistic effects of the Sun. In the first part of my project I set about achieving the value of the precession of Mercury using the Euler-Chromer method to simulate Mercury’s orbit and least-square linear fits of $\frac{\delta(\theta)}{\delta(t)}$ and precession rate vs. $\alpha$ . I achieved a value of $47.4685 \frac{arcseconds}{century}$ , with a percent error deviation of 10.39 from the true value, $43 \frac{arcseconds}{century}$ .

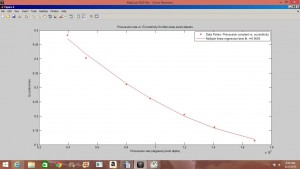
In the second part of my project, I let the eccentricity of the orbit of a Mercurian-sized body vary in its orbit in order to observe eccentricity’s effect on the precession rate. I determined that precession rate is inversely proportional to $e^{2}$ . The values of $\alpha$ and eccentricity I used are included in a table attached to this post.

This past week I experimented with 3-body systems in order to determine the effect of Jupiter on Mercury’s precession. Using the Euler-Chromer method I was able to successfully model a Jupiter-Mercury-Sun system, but only when the Sun’s position and velocity were held at 0.

For the case in which the Sun was to be given an initial position and velocity, I input parameters that should have allowed the center of mass to remain constant, however the graphs showed the Sun escaping from the solar system. Unfortunately I’m not sure how this error occurred, however I am convinced that this model is necessary to determine Jupiter’s effect on Mercury’s precession, as I was unable to achieve the correct value with the model in which the Sun’s position and velocity were held constant.

Link to Code:
https://docs.google.com/a/vassar.edu/document/d/1DrX3F-mnJsyuq8FPltXRY8aCFyNxQvoUGUG_BoIpiBE/edit?usp=sharing

Link to Eccentricity Data:
https://docs.google.com/a/vassar.edu/spreadsheets/d/1YNlhVNkyhy-arqPQW5dAoME6pCHRKIlXpKaZ6bisG-s/edit?usp=sharing

Precession of Mercurian Planets: Data and Results

Over the past week I have developed my code to achieve a fairly accurate approximation of Mercury’s precession due to the general relativistic effects of the sun. This was achieved by plotting the orbital motion of Mercury over 7 orbital periods, then saving the locations of the perihelions from each of the orbits. From these perihelions, I was able to graph the precession rate, $\frac{\delta(\theta)}{\delta(t)}$ . For an alpha of 0.0015:

The slope of the linear-squares best fit gives the rate of precession experienced by Mercury at this value of alpha. In order to extrapolate the true precession rate of Mercury (which is very small and would be difficult to calculate using the above method) by graphing the precession rate as would be experienced by Mercury at different values of alpha. (As seen previously, precession rate is given by C*alpha; the relationship between precession rate and alpha should be linear. For Mercury this resulted in the graph:

The slope of this graph (C) was calculated to be $1.1997*10^{4} \frac{degrees}{year*unit alpha}$ ; which is close to the true value, $1.11*10^{4} \frac{degrees}{year*unit alpha}$ . This yielded a precession rate of $47.4685 \frac{arcseconds}{century}$ , as compared to Mercury’s true value, $43 \frac{arcseconds}{century}$ . This corresponds to a percent error deviation of about 10.39.

After completing this extrapolation, I began an investigation into the effect of eccentricity on the precession of the perihelion of a planet’s orbit. I left the both the mass and perihelion values for my test planet to be the same values as for Mercury, however I allowed the semi-major axis length and eccentricity values to vary. Holding the perihelion constant at the value of Mercury’s perihelion results in the expression $e=1-0.31 \frac{AU}{a}$ , where e is the eccentricity and a is the semi-major axis length in astronomical units. Using the same method as given above, I was able to calculate the precession constants C for 7 different Mercurian systems, each with a different value of eccentricity. The results are shown below:

As can be seen by the graph, the best fit for this set of data is a multiple-linear regression fit, of degree 2. Checking this result with Einstein’s expression for the precession rate:

$\epsilon=24*\frac{(\pi^{3})*(a^{2})}{(T^{2})(c^{2})(1-e^{2})}$

We see that the precession rate is indeed inversely proportional to $e^{2}$ .

Here is a link to my updated Mercury Precession code:
https://docs.google.com/a/vassar.edu/document/d/1fw8L5ZvhqMMVMYltkJH6Ac425KrmnbbDUJs_6GV7aPI/edit?usp=sharing

And a link to my Mercurian Eccentricity code:
https://docs.google.com/a/vassar.edu/document/d/1eqEBSExnBQZRgFUq9GYQDdjTqC9EODRIR0llXQv7sMw/edit?usp=sharing

References:

Computational Physics by Nicholas J. Giordano and Hisao Nakanishi

Vankov, A.A. “Einstein’s Paper: Explanation of the Perihelion Motion of Mercury from General Relativity Theory”.

Preliminary Results: Precession of Mercurian Planets

This week I worked on the modeling of Mercury’s orbital motion around the Sun. Using the Euler-Chromer Method and the general relativistic force law (see previous post for a more quantitative description) I was able to create a code that shows Mercury’s movement over several orbits. The value for alpha was used at 0.01 (very much greater than the true value) and that the initial conditions used were when $r_{I}=0.47 AU$ , and $V_{I}=8.2$ $\frac{AU}{year}$ . It is clear over several orbits that the location of Mercury’s perihelion is changing.

In the following plot, the different positions for the aphelion (chosen for clarity) are clearly shown by lines connecting the origin (or the Sun) to the aphelion.

It is my next goal to determine the amount of degrees by which the orientation of this orbit changes over time. I have run into the issue that Matlab’s acos and asin (arccos and arcsin) functions give imaginary values if their inputs are not with the range of -1<x<1. When this issue is resolved, I will be able to finish deriving the precession rate of Mercury, and will proceed to experimenting with the eccentricity of Mercurian planet orbits and their resulting rates of precession.

Here is a link to my Matlab code: https://docs.google.com/a/vassar.edu/document/d/1fw8L5ZvhqMMVMYltkJH6Ac425KrmnbbDUJs_6GV7aPI/edit?usp=sharing

Precession of Mercurian Planets: Project Plan

Goals:

Week 1: Preliminary Results

As a check to make sure my code will run correctly, I will first model the precession of Mercury’s orbit as caused by the Sun. I must first write a code that will model the movement of a Mercury through it’s orbit according to Kepler’s laws. The force law predicted by General Relativity is given by:

$Fg=\frac{GM_{s}M_{m}}{r^{2}}(1+\frac{\alpha}{r^{2}})$

where G is the Gravitational constant of the universe, Ms is the mass of the Sun, Mm is the mass of Mercury, and a Constant*α gives the rate of precession for the orbit. For the case of Mercury, $\alpha=1.1*10^{-8} AU^{2}$ .

Applying the Euler-Chromer method to the above equation to approximate the x and y velocities and positions of the planet as it travels throughout its orbit yields:

$V_{x,i+1}= V_{x,i}-(4*(\pi^{2})*x_{i})/(r_{i})^{3}+(\alpha*4*(\pi^2)*x_{i})/(r{i})^{5})*\Delta(t)$
$x_{i+1} = x_{i}+(V_{x,i+1})$
$V_{y,i+1}= V_{y,i}-(4*(\pi^2)*y_{i})/(r_{i})^{3}+(\alpha*4*(\pi^{2})*y_{I})/(r_{I})^{5})*\Delta(t)$
$y_{i+1} = y_{i}+(V_{y,i+1})$

Where the initial conditions are (assuming $r_{1}$ to be at the planet’s aphelion):

$v_{1} = \sqrt(\frac{G*M_{s}*(1-e)}{a*(1+e)}$
$r_{1} = (1+e)*a$

where a is the semi-major axis length of the planet’s orbit.

In Computational Physics, Giordano and Nakanishi find the precession of Mercury by first finding the precession rate for a much larger value of $\alpha$ , because it is difficult to measure the precession for a value this small (it would require computing the motion for hundreds of thousands of years). Using different values of α give different values for the precession rate, and graphing these two parameters against one another will provide the desired constant C. Once C is obtained, I can multiply this number by α to get the true precession of Mercury caused by the Sun.

Week 2: Results with Data Analysis

Once this code is working correctly, I can modify the initial conditions for the orbital motion portion of the code to represent new orbits. (Changing the parameters a, e, but maintaining the value of the perihelion as that of Mercury, so that I may compare my results to that for Mercury.)

If I have extra time I will add in other planets to the original Mercury-Sun system to observe the resulting effects on Mercury’s precession.

Week 3: Finalize project: make sure the code’s comments are informative and helpful, and review the program/results for any mistakes.

Week 4: Provide constructive criticism to other students on their projects/Prepare for project presentation.

Week 5: Give my project presentation to the class.

References:
Computational Physics by Nicholas J. Giordano and Hisao Nakanishi

Computational Physics Project Proposal

For my computational physics project I would like to investigate the relationship between the precession and the eccentricity of a planet’s orbit due to general relativity as detailed in chapter 4, section 3 of Computational Physics, by Nicholas J. Giordano and Hisao Nakanishi. Precession is the phenomenon of the rotation of the orientation of axes of a planet’s (elliptical) orbit with respect to time caused by the gravitational forces exerted by other planets. However, general relativity predicts deviations from the inverse-square law, which (for example) allows the Sun to contribute an additional 43 arcseconds per century to the precession of Mercury (as the distance between the two is small enough for the deviations to have an effect). The rate of precession examined in this project will only be that which is caused by the model planet’s host star. This will entail the construction of a planetary motion program using Newton’s law of gravitation and the Euler-Chromer method; which will later be adjusted to allow for the addition of a variable precession rate. The value of the planet’s perihelion will be held constant at the value for Mercury’s perihelion, but the eccentricity and size of the orbits will be allowed to vary. Mass of the planet will be held constant, at the same value as for Mercury.
If I have additional time left over I could also add another planet (such as Jupiter) to my code to make a three-body simulation of the “Mercury-like” planet.

Modeling and Experimental Tools with Prof. Magnes

Ideal for getting ideas and feedback on upper level physics tools.