Outline:

1. Questions from Comments

2. Analysis of our Neural Network

3. Concluding Remarks

4. Future Plans

1. Questions from Comments:

In this section, we will be answering the questions we received from our last post.

1. It seems that not every neuron is connected to EVERY other neuron since there are different connection pattern.
2. When you say an energy of “-5000″ what are your units/reference point?  I am still wondering how and why the Monte Carlo Method works and how the energy state is so low for ordered systems.  This may be unrelated and somewhat random, however, why is it that entropy (disorder) in chemistry always increases and is actually considered a lower state of energy?

Every neuron in our neural network is connected to one another. The results of their connection can be found within the j-matrix; each pattern has it’s own j-matrix.  When we store multiple patterns in one system, separate J matrices are created for each pattern, but the J matrix that is used (J_total) is the element-wise average of the separate J matrices.  So, for each neural network there is only one J matrix, which describes the connections between each neuron and every other neuron.

When a pattern is greatly distorted it takes more energy to return it back to the desired pattern. However, entropy states that the greater the disorder the lower the state of energy. Our neural network is an artificial system that has no relations to entropy. Our energy state for ordered patterns is less than that of disordered patterns because that is the way our code is designed. Furthermore, our j-matrix is designed so that when we calculate the energy of stored patterns it gives us a large negative value for energy. However, when we calculate the energy of disordered patterns it gives us energies close to zero.  The energy calculated in our neural network does not have units; it’s similar to intensity where we are just concerned with the relative energy between the neurons. The Monte Carlo method simply goes through a distorted pattern and determines whether or not a neuron needs to be flipped. This decision is based on the input of one neuron from the summation of the inputs of  the other neurons within the neural network.

2. Analysis of our Neural Network:

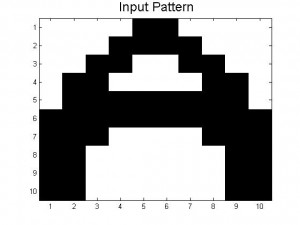
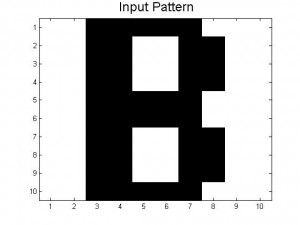
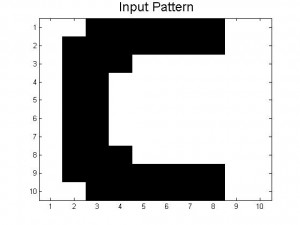
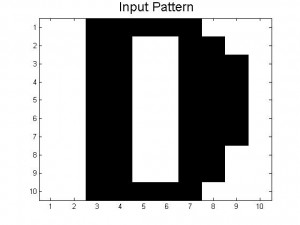
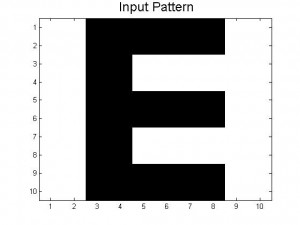
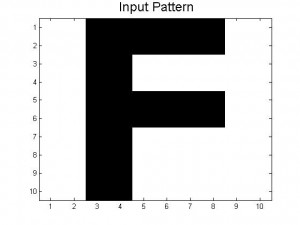
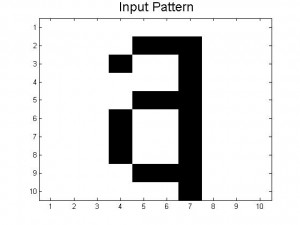
Since our last post we have created neural networks with a larger number of patterns stored, in an attempt to study the system as it begins to fail correct memory recall.  The way we accomplished this was by building systems with more letters as stored patterns.  We had a system which stored A-C, one which stored A-D, and one that had A-F and also a lowercase letter a.  Pictures of all of the letters we used as stored patterns are shown below.

Below are the 7 stored patterns within our neural network.

            

These systems (and links to their codes) are discussed below, but first a little background on the storage of many patterns in neural networks.

As explained in our previous posts, storing more patterns in a neural network causes these patterns to become more unstable: if you think of the energy energy landscape picture from our last post, the minima associated with each pattern become shallower the more patterns that are stored.  This occurs because of the averaging of all the J matrices that correspond to the individual patterns that we want to store: each new pattern distorts parts of the other patterns.  This can be seen visually in the pictures of the J matrices in our last post; the combination of A and B is much more complicated than A and B on their own.

Our textbook (Giordano and Nakanishi) talks about the limitations of how many patterns can be stored in a neural network.  The main obstacles are that 1. any patterns that are too close to each other will likely interfere, and 2. there is a theoretical limit at which the system changes and all patterns become unstable.

For 1., think of the energy landscape again, as well as the letters we use.  The minima for the letters B and D will be relatively close together on the energy landscape because they are relatively similar patterns, and thus their troughs will likely merge a bit and may produce patterns somewhere between the two.  We run into exactly this problem with our A-D code, which often works for A and C (as long as they are not too distorted, usually less than 0.3 or so), but which usually returns a pattern somewhere between B and D when given distorted inputs of B or D.

  

If you want to try this out for yourself, use the code below.

Link to Code: Stored Patterns A-D

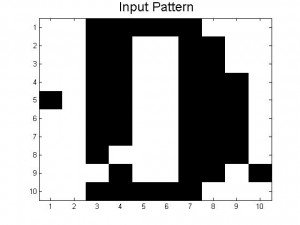
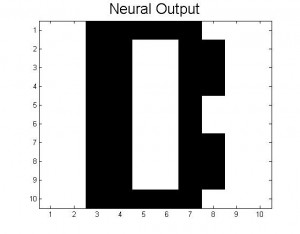
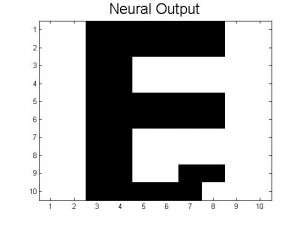
The theoretical limit of the number of patterns that can be stored is given in the text as ~0.13N (in our case, 13 patterns).  Our neural networks begin to function very poorly once we store 7 patterns (A, B, C, D, E, F, a); beyond simply confusing the letters that are similar, nearly all inputs lead to the same answer, a strange hybrid of letters (mainly F and B it seems), shown below.

  

This code actually does work for some inputs (if given an A distorted by 0.1 or less, successful recall of the letter A is usually achieved).  However, nearly all inputs, even those unlike any other pattern (such as the lowercase a) give the same jumbled result seen above.  This is likely a combination of the two effects mentioned above: many patterns here are similar to each other, and the number of patterns has significantly lessened the deepness of the minima associated with each pattern, leading to more instability across all of the stored patterns.  Ideas for how to get real systems closer to this theoretical limit of 0.13N are discussed in Future Plans.

Try this out for yourself with code below.

Link to Code: Stored Patterns A-F + a

We were able to create a very functional neural network that stored three patterns, A-C, which avoided almost all of the problems of having patterns too similar to one another and having so many patterns that the energy landscape minima become too shallow.  The link to this code is below.

Link to Code: Stored Patterns A-C

3. Concluding Remarks:

We started this project in wanting to answer these questions:

1. How far away initial inputs can be from stored patterns while maintaining successful recall.
2. How many patterns can be stored in the neural network.  The book discusses the maximums associated with this type of neural network, but we will investigate why this limit exists, as well as what kinds of behaviors change around this limit.
3. How long (how many Monte Carlo iterations) recall of stored patterns takes.

During the time spent on this project we were able to answer the above questions. However, we also ran into several unexpected problems and results. We found that the most we could distort a pattern is by roughly flipping 45% of the pattern, in order for our code to still work. Patterns that were distorted by 50% no longer worked and the image output was not recognizable. These numbers are based on a neural network with just three patterns: A, B, and C.

Several patterns can be stored in the neural network, however in order to have a neural network that works, we could only store 3 of our 7 patterns. This is so because after C, the letters become very similar to one another; for instance B and D or E and F. With these similarities the neural network produces output patterns that are half way between the similar letters, instead of one letter.  If we had 7 patterns that were all drastically different from one another, we believe that our neural network would work.

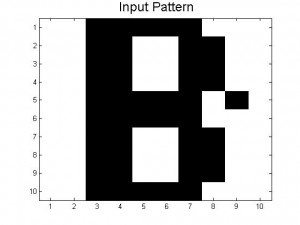
The amount of Monte Carlo iterations is highly dependent on the amount of patterns stored in our neural network and by how distorted a pattern is. In our code we set a limit of 1000 iterations where the program stops if it is taking 1000 Monte Carlo sweeps to achieve the desired pattern. If a program takes 1000 iterations it means that the desired pattern we want is not going to be produced. This is where you get patterns that are incomplete or half way between two letters. When our neural network was successful it only took 1 Monte Carlo iteration to give us the desired pattern. Below is a picture of a distorted B and the output result after 1000 iterations, which is a pattern between B and D. As you can see the distorted B is very close to  the letter B, however because this neural network has D stored as a pattern, it can not make up it’s mind as to which letter to display.

   

 

4. Future Plans:

One of the main things we would want to do next is to create a neural network with more patterns, approaching that theoretical limit of 0.13N.  The best way to do this is likely with patterns that are more orthogonal than the letter patterns we used in this project.  This would be easiest to accomplish with very simple but drastically different patterns, such as vertical lines or circles in different positions.  With these new patterns, we would be able to uncover much more about our neural network than we can now with storing letter patterns that are very similar to one another.

Another objective we would want to tackle is how the size of the neural network affects its function.  Specifically, I wonder if we used the same 7 patterns (letters A-F and lowercase a) but in a neural network that was 15×15 neurons (or even bigger), would we be able to get successful recall of the lowercase a, as we were unable to with our current 10×10 size network?  More neurons (more importantly, a bigger J matrix) should be able to handle more patterns before the energy landscape minima become too shallow, so this should work, in theory.  Testing this would provide us more insight into the limitations on the number of patterns that can be stored in a neural network.