This week I worked on the modeling of Mercury’s orbital motion around the Sun. Using the Euler-Chromer Method and the general relativistic force law (see previous post for a more quantitative description) I was able to create a code that shows Mercury’s movement over several orbits. The value for alpha was used at 0.01 (very much greater than the true value) and that the initial conditions used were when , and . It is clear over several orbits that the location of Mercury’s perihelion is changing.

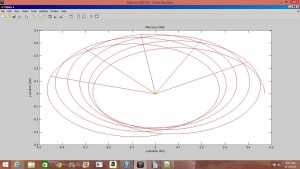
In the following plot, the different positions for the aphelion (chosen for clarity) are clearly shown by lines connecting the origin (or the Sun) to the aphelion.

It is my next goal to determine the amount of degrees by which the orientation of this orbit changes over time. I have run into the issue that Matlab’s acos and asin (arccos and arcsin) functions give imaginary values if their inputs are not with the range of -1<x<1. When this issue is resolved, I will be able to finish deriving the precession rate of Mercury, and will proceed to experimenting with the eccentricity of Mercurian planet orbits and their resulting rates of precession.

Here is a link to my Matlab code: https://docs.google.com/a/vassar.edu/document/d/1fw8L5ZvhqMMVMYltkJH6Ac425KrmnbbDUJs_6GV7aPI/edit?usp=sharing