(Note that equations are rendered in LaTeX which I typed; they simply come through as images, though I include code for documentation.)

My preliminary results were fairly boring, in that I simply executed in MATLAB the guitar simulation central to the first part of chapter 11 of the text. However, this problem was not trivial, and the machinery constructed here will prove critical later in the project.

As background, recall in chapter 6 how the motion of a string was simulated using eq. 6.6:

$latex y(i,n+1)=2[1-r^2]y(i,n)-y(i,n-1)+r^2 [y(i+1,n)+y(i-1,n)]$

where c = speed of wave and r = cΔt/Δx. The force on the bridge (defined here to be the left boundary of the string) can be calculated using eq. 11.4:

$latex F_{\text{bridge}}=T\frac{y(2,n)-y(1,n)}{\Delta x}$

where T is tension, and y(1,n) is the leftmost element on the string at time n (this is a slight modification to the equation in the book, as MATLAB starts indexing at 1, whereas the book’s authors start at 0). For a string plucked at one fifth its length away from the bridge, the following results were obtained after simulating the vibrating string, calculating the force on the bridge with time, and taking the power spectrum of the force using the discrete Fourier transform written for class:

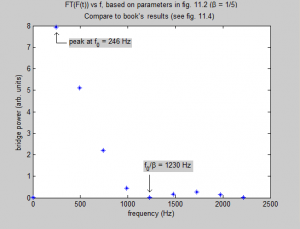
Figure 1: Preliminary data. Bridge power spectrum calculated in MATLAB matches the results in the book very well, indicating that the code used is a good starting point for the rest of the project.

Code used attached here via DropBox (no need to sign up for an account).