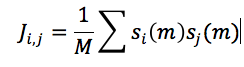Goals and Sources
The goal of this project is to investigate some simple models of neural networks and memory, which are extensively used in cognitive science and related disciplines to model certain aspects of human brains. Our project will follow Section 12.3 of Computational Physics by Giordano and Nakanishi, which draws on the Ising and Monte Carlo methods presented in Chapter 8. This project will be attempting to investigate how to create this type of neural network model, how well it retrieves stored patterns depending on differing input patterns, how many patterns can be stored (and why there is a limit), how well the system functions when parts of the memory are damaged, and how the system learns new patterns.
Background
Chapter 8 introduces the Ising model, which is used to model magnetic substances and phase transitions with temperature changes. The basics of this model are an array of spins, which are allowed only two orientations: up (+) or down (-). These spins are connected to their neighbors so that they influence each other; when a negative spin is surrounded by positive ones, the flipping of the negative one to positive represents a reduction of energy. The Monte Carlo method is used to search through the array, deciding if each spin should be flipped or not, according to its interactions with the surrounding spins, so that the energy of the system tends towards its minimum value.
+ + + + + +
+ – + → + + +
+ + + + + +
Using a 2-D array of completely interconnected Ising spins, a group of neurons can be modeled and investigated. These neurons are very simplified, so that they are in only two possible states, firing (+) or not firing (-). Patterns can be stored in these neural networks by formatting the connections between spins so that stored patterns correspond to energy minima compared to random patterns. This is accomplished with Equation 12.18
where J_i,j is the connection array (which stores all the connection weights between the neuron spins), M is the total number of stored patterns, s_i (m) and s_j (m) are the configurations of spin i and j in stored pattern m.
Project Timeline
Week 1 (4/6 – 4/12)
We will begin by creating an Ising magnet program and learning the Monte Carlo method, following Chapter 8 and relevant examples closely. This will set us up to be able to implement these tools on our neural network models later on.
Week 2 (4/13 – 4/19)
Next, we will create a simplified Neural Network, using symmetric connections and storing relatively few patterns, and test this network so that we are sure it functions as it should. The beginning parts of Section 12.3 will be followed closely here. In this process, we will figure out most of our code, in terms of creating neural networks, how the neurons are indexed, how to create patterns easily using for loops, how to store these patterns using Equation 12.18, etc.
Week 3 (4/20 – 4/26)
Here we will begin splitting up the topics for further investigation. Routes of investigation include
a. How far away initial inputs can be from stored patterns while maintaining successful recall.
b. How many patterns can be stored in the neural network. The book discusses the maximums associated with this type of neural network, but we will investigate why this limit exists, as well as what kinds of behaviors change around this limit.
c. How long (how many Monte Carlo iterations) recall of stored patterns takes.
Tewa will take charge of a and c.
Brian will focus on section b.
Week 4 (4/27 – 5/3)
We will continue to work on the investigations from week 3, and if we have time, we will progress to more complicated neural networks. Some complications we can introduce are larger networks (and how the recall times might change), asymmetrically connected neurons (a more complicated weight connection matrix), and how further learning impacts the neural networks.
Week 5 (5/4 – 5/10)
We will continue any investigations we have left during this week, and begin writing up our results for final blog posts and presentations.
Week 6 (5/11 – 5/13)
We will finish up our blog posts and presentations, and present our results to the class.