Railgun Physics Final Results: A Dangerously Powerful Circuit

As my part of the project, I have successfully modeled how a railgun acts as a circuit. These results are interesting on their own, but throughout this post I will try to put them in context and show the various aspects of my results. In my preliminary data, I had derived the most general versions of the magnetic field of the rails, missing a good amount of necessary information. I modeled resistance, showing how it changes as the factors that compose it change. I will present the rest of my results by first introducing each necessary concept, and then showing how it is applied in one of two scenarios: a small-scale railgun and a military-scale railgun.

IMAG0129

Current from the Capacitor Setup:

As noted before, the original current in the circuit comes from a bank of capacitors of varying degrees of strength. The capacitor has an initial charge:

(1)   \begin{equation*} {Q_0} \end{equation*}

This charge will decrease over time, where

(2)   \begin{equation*} {Q=Q_0e^{\frac{-t}{\text{RC}}}} \end{equation*}

As we can see, the charge in the capacitor decays at an exponential rate proportional to the resistance of the circuit and capacitance of the bank. The higher these values, the longer it will take to discharge.

Now we can see that the current is time derivative of Q,

(3)   \begin{equation*} {\frac{\text{dQ}}{\text{dt}}} \end{equation*}

The result of this derivative is:

(4)   \begin{equation*} {o=\frac{Q_0}{\text{C$\rho $}\frac{(2L+2d)}{A}}e^{\frac{-t}{\rho \frac{(2L+2d)}{A}C}}} \end{equation*}

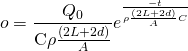
We will use this term “o” to refer to the current from the capacitor. We will model two specific scenarios, a small scale rail gun that we found online, and more massive versions of the rail gun that the military might use. Below is the model for current due to power supply of a small scale version with rails of .2m spaced .03m apart, and cross sectional area .0009m^2 with 10 450 microfared capacitors connected in parallel to store maximum charge.

Here you can see that the current from the capacitor is massive at first. It then drops very immediately over a very short period of time. The majority of the current is gone after a little over a nano second. As you can see, adjusting the length of the rails also causes the current to drop, meaning that as the projectile moves and the length of the rails in the circuit lengthen, the current drops tremendously. The same is true with the resistivity; rails made of aluminum draw a great deal more current than do the rails made from steel, the opposite end of the resistivity spectrum.

Now we will model the most prototypical version of the rail gun proposed and worked on by the navy. According to our research, the rails of this gun will be up to 10m long, spaced .8 meters apart, a cross sectional area of .01m^2, and be supplied by capacitors storing 33 megajoules of energy. Energy Stored in a capacitor is defined as:

(5)   \begin{equation*} {E= \frac{Q^2}{2C}} \end{equation*}

Which, knowing that 33 megajoules of energy is necessary, yields

(6)   \begin{equation*} {Q=8124\sqrt{C}} \end{equation*}

Now we know that these values constrain each other. For example, let’s say we are working with 10,000 coulombs of charge. The corresponding value of C would then be 1.5 Farads.  We will go forward with these parameters from here on out. We will also let the minimum value of resistivity correspond to that of iron, 9.71*10^-8, because it is extremely unrealistic to use aluminum.

Here we see a very similar result to the current from the capacitors of the smaller scale version, albeit on a much larger scale. Here, it is important to see that the current does not decay quite as quickly. This is remedied in the model by making the timescale larger, something that can be done in mathematica.

Induced Current

As we know, the magnetic field in the loop and the area of the loop change as current flows and as the projectile moves. This changes the magnetic flux phi through the loop and induces a potential difference (aka EMF) epsilon and hence an induced current, which we will refer to as u. We must first find the EMF of the system.

(7)   \begin{equation*} {\epsilon =\frac{-\text{d$\phi $}}{\text{dt}}} \end{equation*}

We must first define:

(8)   \begin{equation*} {\phi =\int B\cdot \text{da}=\int B\cdot \text{dxdy}} \end{equation*}

Now I will take the time derivative of \[Phi]. B is changing over time so:

(9)   \begin{equation*} {\frac{\text{d$\phi $}}{\text{dt}}=\int \frac{\text{dB}}{\text{dt}}\text{dxdy}} \end{equation*}

B doesn’t expressly depend on t, so we will use the chain rule:

(10)   \begin{equation*} {\frac{\text{dB}}{\text{dt}}=\frac{\text{dB}}{\text{dL}}\frac{\text{dL}}{\text{dt}}} \end{equation*}

Here is where the math begins to get a little dicey, and the readers will have to trust what I am doing. I have posted the link to my mathematica documentation at the bottom of this page; if anybody would like a more detailed look at the derivations I have done, then they can look there. In the meantime, I have solved for the EMF of the loop following the procedure listed above:

(11)   \begin{equation*} {\frac{1}{4 \pi }i \mu _0 v \left(-\log \left(L \sqrt{a^2+L^2}+L^2\right)+L \log \left(\sqrt{(d-a)^2+L^2}+L\right)-\log \left(L \sqrt{(d-a)^2+L^2}+L^2\right)+\log \left(L \sqrt{a+L^2}+L^2\right)\right)} \end{equation*}

We can see here that EMF is actually dependent on the NET current through the wire, which is problematic at first. However, as we discovered later on, we can account for this with relatively simple algebra. This logarithmic function, which increases as L decreases, is very important. However, its current form is far from elegant and from here on out we will refer to it as k. Dividing this result by R will give us the induced current (which we will refer to as U) and yields the following expression:

(12)   \begin{equation*} {\frac{\epsilon }{R}=U=\frac{1}{4 \pi \rho (2 d+2 L)}i A \mu _0 v k} \end{equation*}

The total current (which we shall refer to as J) in this scenario is the original current coming from the capacitor minus the induced current caused by the changing magnetic flux and thus emf. We know this to be true from Lenz’s law, which shows us that the induced current lessens the overall current and thus the overall magnetic field and eventually force. Once again, the algebra for the derivation of J is in my documentation. If you would like to see it, it is attached at the bottom of the page. For now, the final result for J will suffice:

(13)   \begin{equation*} {J=\left(\frac{A Q_0 e^{-\frac{A t}{C \rho (2 d+2 L)}}}{\text{C$\rho $} (2 d+2 L)}\right)/\left(1+\frac{1}{4 \pi \rho \_ (2 \text{d$\_$}+2 \text{L$\_$})}A \mu _0 v k\right)} \end{equation*}

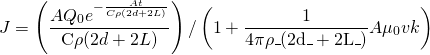
Once again, I would like to model this situation for two different scenarios, the first being a rail gun with a=.0009, d-.03, C=450*10^-5, and Subscript[Q, 0]=1.8.

As we can see from the model, an increase in velocity drastically decreases the current in the loop. This makes a lot of sense, because a higher velocity means a higher change in flux with respect to time, and thus a much greater inducted current in the opposite direction. This velocity term is something I would like to be able to solve for as a function of time in the future, but for now I will allow it to be a manipulated quantity.

As before, I will now model the total current for a military grade railgun.

Once again, we see a very similar result. I have set the range of velocities much higher for the military grade railgun. The military hopes to speed velocities as high as 2400 m/s, and I have obliged them in my model.

EMF Revisited

Now that we have come up with an expression for current, we can plug it back into the expression for EMF. Which we will then attempt to plot as a model of time and length. Plugging our expression for current yields:

(14)   \begin{equation*} {\epsilon =\frac{ \mu _0 v k}{4 \pi }\left(\left(\frac{1.8}{(10L+.15)\rho }\right)e^{\frac{-t}{\rho (10L+.15)}}\right)/\left(1+\frac{1}{\rho (.06+2 L)}9.04*10^{-11} v k\right) } \end{equation*}

Using the above equation, I plotted the EMF of the small railgun over time:

The maximum emf is about 200 volts, which makes sense in the context of this study. It is a sizeable, but not intrusive chunk of the Rail’s original potential difference.

As has been the trend, a plot of EMF vs. Time regarding the military railgun:

Back to the Magnetic Field:

Now, the final step in my part of the project is to model the magnetic field that is on the projectile. From here, John will be able to take a closer look at the forces and energy of the projectile. Plugging the total current into my derivation of magnetic field on the projectile:

(15)   \begin{equation*} {B_{\text{projectile1}}=\frac{\text{J$\mu $}_0}{4\pi }b} \end{equation*}

Here, I have defined “b” as yet another logarithmic function, one that appears when integrating the magnetic field over the width of the loop/length of projectile. To see the specific derivations at work, refer to my Mathematica page.

Magnetic field of a small rail gun:

I once again plugged the parameters of the small rail gun into the above equation and created the following model:

Magnetic field of a military rail gun:

Doing the same for the military rail gun I created:

Though I will conclude my project much more thoroughly in my next post, I would like to make a few comments about my final results here. The currents of both railguns was incredibly high, at most many million amps. However, they only exist as such for extremely small periods of time, giving way to the idea of a “pulse” of power, firing the projectile. The analogous magnetic fields reveal similar information. For a very brief period of time, these railguns create magnetic fields stronger than the strongest continuous magnet in the world. However, this magnitude once again disappears almost instantaneously. Numerous factors go into creating extreme power and even more go into deciding when and how it is dispersed. My data provides a glimpse into one of the most fascinating parts of physics. The models are the most interesting part; I implore you to look at the mathematica documentation and play with them, as well as look at my derivations.

https://drive.google.com/file/d/0B0sdNVAIz9CjZUhEUTRnMldBRWs/edit?usp=sharing

Share

1 thought on “Railgun Physics Final Results: A Dangerously Powerful Circuit”

  1. Avatar photoJenny Magnes

    Nice job on the simulations. You do need to label your axis and clarify the units. I assume that the B-fields are in mT? You may want to provide a link to John’s post for specifics on the circuit.

Comments are closed.