I have developed expressions for B, H, and M for the JET tokamak, and have plotted these fields.  I began by deriving the expression for the magnetic field of such a system, approximating it as a toroidal solenoid.  I followed Griffith’s example 5.10 to arrive at my expression.  As mentioned previously, the expression for the magnetic field of this system is:

$\textbf{B(r)} = \frac{\mu_{0} N I}{2 \pi s} \hat{\phi}$.

As mentioned previously, I use the parameter values from the JET project, and will assume that $N = \alpha q(r)$.  My first instinct (and the first value of alpha that I tried) was to set $\alpha$ at the circumference of the torus (17.9 m).  As will be discussed below, this did not give reasonable results, and I revised the value of alpha accordingly.

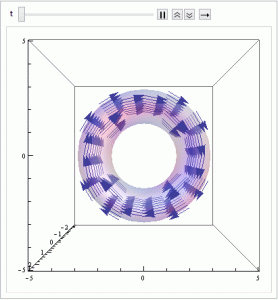
I defined a field (bfield) based on the expression I derived.  This was in spherical coordinates since that was easiest to use with the Mathematica command TransformedField.  I then transformed this to Cartesian coordinates, and used VectorPlot3D to plot the Cartesian vector field.  This produced the circumferential field that I expected.  It varies only with distance from the center of the torus ring, and curves around the torus.

The magnetic field, as expected, is purely circumferential and its direction alternates as the current changes. The torus has been superimposed on the field to indicate the region where the field is nonzero.

The torus from a different perspective.

I then repeated the same procedure for the Auxiliary field and magnetization, and both produced the fields I expected (both were the same shape but different magnitudes than the magnetic field and the magnetization was in the opposite direction).  Magnetization was in the opposite direction of the magnetic field (as expected) because I used the magnetic susceptibility value of hydrogen (since JET used an H or DT plasma) and hydrogen is diamagnetic (as per Griffiths Table 6.1).  A tacit assumption here is that this value does not change significantly when the gas is ionized into a plasma.  I do not know what effect this would have on my results, but my results should be viewed with this fact in mind.

The Auxiliary field looks very similar to the magnetic field, and, in fact, differs only in that the vectors have different magnitudes.

Note that all of these fields are identically zero for all regions outside of the the volume of the torus.  The values described by the vector field only hold for locations where $(R – r/2) \leq s \leq (R + r/2)$.  Unfortunately, I was unable to find a way to force Mathematica to either make the vector field zero in this region or two suppress the vectors so that they did not display.  Despite this, the field is correct, just over an incorrect range.

The magnetization in the torus, again, has the same shape as the other fields, but opposite sign.

Now, realistically, the current in my expression for these quantities would not be constant, but would vary with time (as tokamaks operate as pulsed, AC devices).  This means that $I = I_{0}\cos(\omega t)$.  This assumes that that at time zero, the current amplitude is maximum (which is reasonable since the zero point is arbitrary as long as we look at the system sufficiently long after the tokamak operation has begun).

To account for this time dependence, I let $I = I_{0}$ and multiplied in the cosine term.  I did this in the VectorPlot3D argument instead of in the definition of my field because the transform would not work with 4 variables.  This should not affect the results.  I did this for all three fields.  As expected, the fields retain their shapes and the vectors alternate direction with current.  An example follows, and the rest can be found in the Mathematica notebook:

Magnetic Field Animation

After developing these models, I wanted to use my expression to find the magnetic field at the center of the torus volume.  I would then compare this to the established value for JET’s magnetic field, and the difference would speak to the legitimacy of my model and the assumptions I made, specifically the proportionality constant, $\alpha$.  The magnitude of the magnetic field as a function is radius was plotted, to emphasize the fact that it varies only with radius and is not constant throughout the torus (since it spans a range of radii).

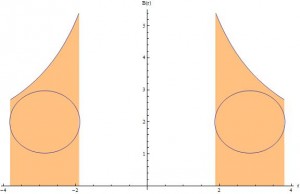
The magnetic field strength as a function of radius, to illustrate the fact that the field does vary with radius, which is not necessarily clear from the vector fields. . The surface of the torus is included to illustrate the region with nonzero field.

For $\alpha = 17.9$, $B = 22.6$T.  The established value is $B = 3.6$T.  This is a percent error of over 500%.  Since this value of alpha was simply a first guess to see how the model worked, this extremely high percent error should not be alarming.  We can easily find a better alpha.  Knowing what B should be, and the other constants, we can solve for alpha and get that it should take a value of $\alpha = 2.85$.  This is very interesting because this means that $\alpha = R$ and that $N = \alpha q = R q = (2.85)(3) = 8.55$.  A value of 8.55 for N means that there are only about 9 windings of the current around the solenoid.  In Griffiths’ example, he specifies that we assume the windings to be “uniform and tight enough so that each turn can be considered a closed loop.”  8.55 turns around a circumference of 17.9 meters is probably not sufficiently tight.  As such, this model has shown that is model is insufficient to describe the behavior of a tokamak (which is not surprising).  As it is, this results indicate our model is imprecise. It also indicates that, perhaps, the current should be modeled as a set of smaller currents with tighter windings superimposed on each other.  The next logical step in this research would be to examine what exactly the effects of this fallacious assumption are, and how best to address them.

I would also like to note that, while my original plan was to also model the electric field of this system.  In my research I have not found any mention of the electric field of a tokamak reactor, only ever the magnetic field.  I assume that this is because the magnetic field is the source of confinement, and thus more interesting. Since the electric field seems to be uninteresting to tokamak research, and since I have nothing against which to compare my model, I will not be modelling this field.

With this model (assuming that the windings were closed loops) changing q had a relatively small effect.  According to the expression for magnetic field, changing q changer the magnitude of the field vectors (they are directly proportional).  In my Mathematica animations of this, though, the change in vector magnitude was never actually noticeable.  As such I conclude that, while the safety factor plays a significant role in tokamak design, due to the simplifications made in my model, it has very little effect.

While my results (that N is small and that q  has a negligible effect) both indicate that my model is not sufficiently precise to model a tokamak, this does not indicate failure.  The main thing that can be learned from this is that a tokamak’s magnetic field is much more complicated than that of a toroidal solenoid, as the current is at a large angle compared to the plane in which the torus lies as it travels around the torus.  While my model is imprecise and does not take this into account, it can produce the appropriate values for magnetic field, but with a compromise.

The assumption that went into my model (Griffiths’) that the current loops were essentially closed meant that we assumed the current had only z an s components (and no phi component).  The fact that N is so small relative to the circumference means that the current loops will be more slanted and will have a component in all three directions.  Obviously, this means that the expression for magnetic field will be different.  In the derivation, the fact that the current had no phi component meant that terms cancelled out, leaving us with a purely circumferential field.  Clearly, in an actual tokamak, this is not the case.  While it is unfortunate that my results showed my model to be insufficient for a robust model of a tokamak, it has been very valuable in that it has confirmed and emphasized the complexity of a tokamak magnetic system.  It also puts the current state of fusion research in a very clear context – research has been going on since the middle of the last century, and yet no viable commercial fusion reactor has been developed.  This seems to make sense considering the complexity of the systems.

—

Here is a link to the Mathematica Notebook: https://drive.google.com/file/d/0B-C9MvBAfmyIc01BdHRRbGxoRW8/edit?usp=sharing