From Biot-Savart law of a wire in a closed loop can be broken into 4 parts. Additionally, it should be noted that when considering Ampere’s Law:
![]()
The displacement current term is expected to be negligible. That is because in order for the instantaneous rate of change of the electrical field to be significant, the power, loop size and switching rate would have to be extremely, large, small and fast, respectively. Furthermore, for a railgun that size, the current term dwarfs the displacement term by several magnitudes, rendering it irrelevant.
Where z is the shortest distance from a point in space to the wire and theta and phi are the angles between the beginning and end of the wire, respectively. Modeling the circuit as four line currents then allows us to break the B field into four components and solve the above equation, yielding:
It should be noted that L is the distance from the start of the rail to the slug and is time dependent, x is the distance along the rails, d is the separation between the rails and y is the distance from the bottom rail. Combining these terms using the law of superposition gives the total magnetic field at any point within the loop.
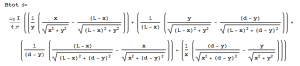
However, since we are interested in the magnetic field on points within the slug, however, we can set x=L and remove the Bback and Bslug term. The removal of these terms originates from the fact that the nonrail sections are far removed from the slug and generate no significant field within the loop. Additionally, the Bslug term can be removed since due to conservation of momentum, the external magnetic field upon the slug can not be generated by the slug. Additionally, in order to ease calculation, we assume the slug is thin in the x direction, so that we do not have to include width considerations in our calculations. Therefore the Magnetic field upon a point within the the slug (hereafter referred to as B) is:
Next, we will calculate the force upon the slug. Using the Lorentz force law, F=I(dlxB). Since railguns are extremely high energy devices, using enormous currents withing the rails while firing, the best way to power these devices is using capacitors. As a result, the current is variable with time as the capacitor discharges. Additionally, as a result of Faraday’s law, there is an emf generated in the loop as the current and loop size vary, which also affects the current as a function of time.
The force direction is determined by the right hand rule between the direction of the current and the B field within the slug. For a counter clockwise current, the current flows in the positive y direction and the B field for all wire components, including the back and slug, point in the positive z direction (out of the page in the diagram), giving a right hand rule direction of +x.
Additionally, the B field described above is for a specific location along the projectile, and as such the B field must be integrated over the width of the slug. The total magnetic force on the slug therefore becomes:
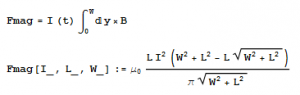
The magnetic force can also be used in Newton’s Second law to solve for the current in the slug. Of course, this is entirely inaccurate, as there are several means for the current to change, including thermal radiation, rotation and voltage gaps between the slug and the rails. These effects are difficult to calculate and not the subject of this project, suffice to say that the most common method of dealing with these forces is to see what portion of the force is lost.
Since L is time dependent, and extremely fluid, the most common way of reducing this equation is to take the spatial terms and group them into a quantity called the inductance gradient. This quantity is the result of the complex induction effects within the circuit, and is dependent upon the waveform of current, geometry of rails, materials of rails and projectile This quantity, however, cannot be determined theoretically. There are not enough governing equations to solve for L. Instead, what papers concerning railguns use are complicated regression models to determine the optimum dimensions for the rails to maximize this inductance gradient, some of which will be modeled using mathematica in the final data. Therefore, the instantaneous force on the slug can be modeled as:
The Current, being modeled by Elias Kim, can then be inserted into this equation to provide an instantaneous force upon the projectile as a function of t, which can the be solved to (hopefully) provide equations of motion for the slug, and at the very least provide a unsolvable differential equation.
In this reduced form, it becomes clear that the most important factor in this equation is the current, which exponentially increases power as it is made bigger. The 1/2 scalar multiple is the result of the common approximation that half of the current in the loop is required to maintain the expanding magnetic fields, and that only the other half produces force. The navy recently tested a gun that fired a 3.2kg slug over mach 7, this gun used over 33MJ of energy.
As for our physical construction, we had some “technical” difficulties with our design and the small issue of it firing a lethal projectile with highly expensive, dangerous materials. As such we are currently working to scale down our design and will construct it and test this weekend, posting the final specifications and results during the final data.
Mathematica Notebook: https://drive.google.com/a/vassar.edu/?tab=mo#folders/0B0K4JjJfDy1fNnE4MHJON0k4TDg
References:
http://web.mit.edu/mouser/www/railgun/physics.html
Elias Kim
http://ikiu.ac.ir/public_files/profiles/items/1295865343.pdf
http://www.livescience.com/7463-navy-tests-incredible-sci-fi-weapon.html

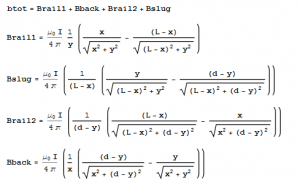
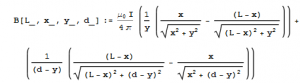
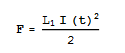

I very much like the extensive commenting on your Mathematica code. You do need to fix the Latex coding and only post work that is original and produced by you; i.e. any figures or videos that are not produced by you have to be taken off the site.