Update: See Conclusion
My preliminary results demonstrate the convolution of two arbitrary functions. There are two ways of convoluting functions in Mathematica. The first method is through a tool called ‘Convolve’, and the second method is through the product of two Fourier transforms as discussed in the previous post.
Example 1:
In this example I will demonstrate the convolution of two Gaussian functions of arbitrary widths:
![]()
The first method is simple. Plug in the two equations into the command ‘Convolve’ along with the necessary parameters. When I did this I got the function:
![]()
The second method requires finding the product of the Fourier transforms of the functions, then taking the Fourier transform of the product. The Fourier transforms of the two functions are as follows:
![]()
Taking the Fourier transform of the product of these two functions and ![]() , yields:
, yields:
![]()
Both methods yield the same result, which is what should happen every time.
Example 2:
In theory any convolution of two functions adheres to the relationship:
![]()
Using paper and pencil and a lot of free time will demonstrate that this relationship is true. In practice, using a computer program to do the work for you could lead to some issues. Mathematica is limited by the sophistication of its algorithms, and convoluting simple functions can only take you so far. In this example I will demonstrate the limitations of Mathematica. Here I will be using the following functions:
![]()
The unitstep function is the Heavyside step function which constrains the exponential function to the first quadrant. Convoluting the two yields the following function:
![]()
The second method gave a slightly different result. Taking the Fourier transform of each function, multiplying them together, and then taking the Fourier transform of that function yielded:
![]()
Both methods worked in the previous example, but here there is a sign change. I tried many different combinations of functions, and most of the time the two convolutions did not match. In fact, most of the time the first method did not give a clear result at all. Sometimes it did not compute the convolution, and sometimes the answer was obviously ridiculous. Fortunately, the latter method always gave an answer. To check to see if the latter method is reliable I redid the calculation using actual data points. I could not do the former method in a similar fashion because no such appropriate tool exists.
I used the ‘Table’ tool to give me a set of values from the two functions above. Here are the plots of the two data sets :
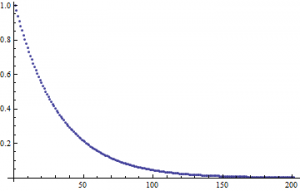
Taking the Fourier transform of each function yields complex values, and so I cannot graph those. The plots of the square of the Fourier transforms are not interesting. After going through with the latter method I came up with this plot:
This result is the same as in the previous attempt through analyzing functions. Considering Mathematica is well suited to handle data, and has a large library of Fourier analysis tools, I am confident that this method will provide the proper results for my future work.
Future
My next attempt will be to demonstrate the convolution of two optical filters. Thorlabs provides raw data of the transmission percentage as a function of wavelength for each filter. I will use the latter method to convolute the two filters, an then discuss how one would try to attempt to deconvolute the convolution.
Mathematica Script


Good work so far. You do need to make your Mathematica file publicly available.