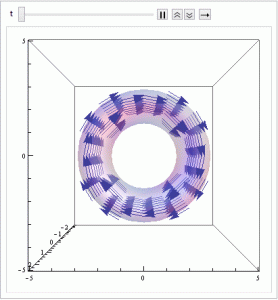
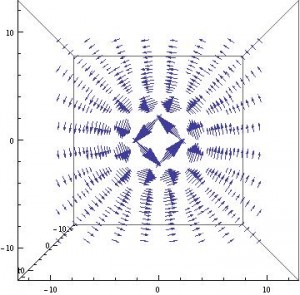
I have developed expressions for B, H, and M for the JET tokamak, and have plotted these fields.  I began by deriving the expression for the magnetic field of such a system, approximating it as a toroidal solenoid.  I followed Griffith’s example 5.10 to arrive at my expression.  As mentioned previously, the expression for the magnetic field of this system is:

$\textbf{B(r)} = \frac{\mu_{0} N I}{2 \pi s} \hat{\phi}$.

As mentioned previously, I use the parameter values from the JET project, and will assume that $N = \alpha q(r)$.  My first instinct (and the first value of alpha that I tried) was to set $\alpha$ at the circumference of the torus (17.9 m).  As will be discussed below, this did not give reasonable results, and I revised the value of alpha accordingly.

I defined a field (bfield) based on the expression I derived.  This was in spherical coordinates since that was easiest to use with the Mathematica command TransformedField.  I then transformed this to Cartesian coordinates, and used VectorPlot3D to plot the Cartesian vector field.  This produced the circumferential field that I expected.  It varies only with distance from the center of the torus ring, and curves around the torus.

The magnetic field, as expected, is purely circumferential and its direction alternates as the current changes. The torus has been superimposed on the field to indicate the region where the field is nonzero.

The torus from a different perspective.

I then repeated the same procedure for the Auxiliary field and magnetization, and both produced the fields I expected (both were the same shape but different magnitudes than the magnetic field and the magnetization was in the opposite direction).  Magnetization was in the opposite direction of the magnetic field (as expected) because I used the magnetic susceptibility value of hydrogen (since JET used an H or DT plasma) and hydrogen is diamagnetic (as per Griffiths Table 6.1).  A tacit assumption here is that this value does not change significantly when the gas is ionized into a plasma.  I do not know what effect this would have on my results, but my results should be viewed with this fact in mind.

The Auxiliary field looks very similar to the magnetic field, and, in fact, differs only in that the vectors have different magnitudes.

Note that all of these fields are identically zero for all regions outside of the the volume of the torus.  The values described by the vector field only hold for locations where $(R – r/2) \leq s \leq (R + r/2)$.  Unfortunately, I was unable to find a way to force Mathematica to either make the vector field zero in this region or two suppress the vectors so that they did not display.  Despite this, the field is correct, just over an incorrect range.

The magnetization in the torus, again, has the same shape as the other fields, but opposite sign.

Now, realistically, the current in my expression for these quantities would not be constant, but would vary with time (as tokamaks operate as pulsed, AC devices).  This means that $I = I_{0}\cos(\omega t)$.  This assumes that that at time zero, the current amplitude is maximum (which is reasonable since the zero point is arbitrary as long as we look at the system sufficiently long after the tokamak operation has begun).

To account for this time dependence, I let $I = I_{0}$ and multiplied in the cosine term.  I did this in the VectorPlot3D argument instead of in the definition of my field because the transform would not work with 4 variables.  This should not affect the results.  I did this for all three fields.  As expected, the fields retain their shapes and the vectors alternate direction with current.  An example follows, and the rest can be found in the Mathematica notebook:

Magnetic Field Animation

After developing these models, I wanted to use my expression to find the magnetic field at the center of the torus volume.  I would then compare this to the established value for JET’s magnetic field, and the difference would speak to the legitimacy of my model and the assumptions I made, specifically the proportionality constant, $\alpha$.  The magnitude of the magnetic field as a function is radius was plotted, to emphasize the fact that it varies only with radius and is not constant throughout the torus (since it spans a range of radii).

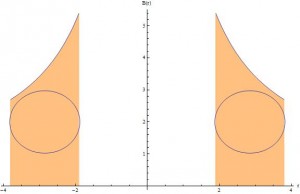
The magnetic field strength as a function of radius, to illustrate the fact that the field does vary with radius, which is not necessarily clear from the vector fields. . The surface of the torus is included to illustrate the region with nonzero field.

For $\alpha = 17.9$, $B = 22.6$T.  The established value is $B = 3.6$T.  This is a percent error of over 500%.  Since this value of alpha was simply a first guess to see how the model worked, this extremely high percent error should not be alarming.  We can easily find a better alpha.  Knowing what B should be, and the other constants, we can solve for alpha and get that it should take a value of $\alpha = 2.85$.  This is very interesting because this means that $\alpha = R$ and that $N = \alpha q = R q = (2.85)(3) = 8.55$.  A value of 8.55 for N means that there are only about 9 windings of the current around the solenoid.  In Griffiths’ example, he specifies that we assume the windings to be “uniform and tight enough so that each turn can be considered a closed loop.”  8.55 turns around a circumference of 17.9 meters is probably not sufficiently tight.  As such, this model has shown that is model is insufficient to describe the behavior of a tokamak (which is not surprising).  As it is, this results indicate our model is imprecise. It also indicates that, perhaps, the current should be modeled as a set of smaller currents with tighter windings superimposed on each other.  The next logical step in this research would be to examine what exactly the effects of this fallacious assumption are, and how best to address them.

I would also like to note that, while my original plan was to also model the electric field of this system.  In my research I have not found any mention of the electric field of a tokamak reactor, only ever the magnetic field.  I assume that this is because the magnetic field is the source of confinement, and thus more interesting. Since the electric field seems to be uninteresting to tokamak research, and since I have nothing against which to compare my model, I will not be modelling this field.

With this model (assuming that the windings were closed loops) changing q had a relatively small effect.  According to the expression for magnetic field, changing q changer the magnitude of the field vectors (they are directly proportional).  In my Mathematica animations of this, though, the change in vector magnitude was never actually noticeable.  As such I conclude that, while the safety factor plays a significant role in tokamak design, due to the simplifications made in my model, it has very little effect.

While my results (that N is small and that q  has a negligible effect) both indicate that my model is not sufficiently precise to model a tokamak, this does not indicate failure.  The main thing that can be learned from this is that a tokamak’s magnetic field is much more complicated than that of a toroidal solenoid, as the current is at a large angle compared to the plane in which the torus lies as it travels around the torus.  While my model is imprecise and does not take this into account, it can produce the appropriate values for magnetic field, but with a compromise.

The assumption that went into my model (Griffiths’) that the current loops were essentially closed meant that we assumed the current had only z an s components (and no phi component).  The fact that N is so small relative to the circumference means that the current loops will be more slanted and will have a component in all three directions.  Obviously, this means that the expression for magnetic field will be different.  In the derivation, the fact that the current had no phi component meant that terms cancelled out, leaving us with a purely circumferential field.  Clearly, in an actual tokamak, this is not the case.  While it is unfortunate that my results showed my model to be insufficient for a robust model of a tokamak, it has been very valuable in that it has confirmed and emphasized the complexity of a tokamak magnetic system.  It also puts the current state of fusion research in a very clear context – research has been going on since the middle of the last century, and yet no viable commercial fusion reactor has been developed.  This seems to make sense considering the complexity of the systems.

—

Here is a link to the Mathematica Notebook: https://drive.google.com/file/d/0B-C9MvBAfmyIc01BdHRRbGxoRW8/edit?usp=sharing

Thus far, I have determined values for the quantities of interest (except for $\mu$ of the plasma) and I have derived an expression for B and H.  I will base the parameters of my model off of the Joint European Torus (as per Albanese, et al., 03; Crisanti, et al., 03). It appears that there will be no D field, since the plasma is a conductor and would not polarize, but simply experience a current.

• $q(r) = \frac{r B_{\phi}(r)}{R B_{\theta}(r)} = 3$
• $r = .95~m$
• $R = 2.85~m$
• $I = 6.0~MA$

I am going to assume that N, the total number of turns, is proportional to the safety factor: $N = \alpha q(r)$ where $\alpha$ will probably be related to the circumference of the torus (which can be found from the radii).

The Biot-Savart Law gives:

$d\textbf{B} = \frac{\mu_{0} \textbf{I} \times \textbf{r} dl}{4 \pi r^{3}}$.

If we assume that the torus is in the x-y plane, centered at the origin, and consider a test point at $\textbf{r}$ and source charge elements at various $\textbf{r’}$.  Then $\scriptr = \textbf{r} – \textbf{r’}$.  Consider a test point on the x-z plane.

Assuming that the winding is tight enough, we can say that $ \textbf{I} = I_{s} \hat{s} + I_{z} \hat{z}$ which, in cylindrical coordinates, is $(I_{s}cos(\phi), I_{s}sin(\phi), I_{z})$.

In evaluating the Biot-Savart Law, we have the term $\textbf{I} \times \textbf{r}$.  Due to the symmetry of the tours, the x and z components cancel out, leaving just a y component.  If the test point is in the x-z plane, this means that the magnetic field will be circumferential, or in the positive $\hat{\phi}$ direction.  The magnetic field can then easily be found using Ampere’s Law:

$\textbf{B(r)} = \frac{\mu_{0} N I}{2 \pi s} \hat{\phi}$

for all points within the minor radius (inside the torus) and

$\textbf{B(r)} = 0$

for all points outside the torus.

From here, it is also easy to find the Auxiliary field, from $\textbf{H} = (1/\mu) \textbf{B}$, so

$\textbf{H} = \frac{1}{\mu} \frac{\mu_{0} N I}{2 \pi s} \hat{\phi}$

inside the torus and

$\textbf{H} = 0$

outside the torus, since there is no magnetic field.

I have also begun work on my Mathematica model.  I began by trying to figure out how to get the vector field to look right, and have been working with a simplified version of my B equation, $\textbf{B} = k/r$.  I have found that the transform to spherical coordinates is easiest to work with (since toroidal geometries do not fit easily into either spherical or cylindrical), which is why my expression uses r instead of s.  This has given the following vector field:

The (simplified) circumferential magnetic field due to a toroidal solenoid (without taking into account the fact that the field is zero outside of the loop of the solenoid).

The vector field is the shape that I need it to be, but I’m having some trouble getting the field to be zero outside of the solenoid.  I tried to use the piecewise function of Mathematica, but keep getting an error.  I think I may need to define two fields (maybe 3) such that they cancel out in the regions where the field should be zero.

The next step will be to input the numbers into my expression, and work out the Mathematica model.  Then I will be able to easily vary q(r) and observe the results.

Link to Mathematica notebook: https://drive.google.com/file/d/0B-C9MvBAfmyIQS12dTZJOGh5bm8/edit?usp=sharing

References

Raffaele Albanese, G Calabr`o, M Mattei, and F Villone. Plasma response models
for current, shape and position control in jet. Fusion engineering and design,
66:715–718, 2003.

F Crisanti, R Albanese, G Ambrosino, M Ariola, J Lister, M Mattei, F Milani,
A Pironti, F Sartori, and F Villone. Upgrade of the present jet shape and vertical
stability controller. Fusion engineering and design, 66:803–807, 2003.

Griffiths, D. J., & Reed College. (1999). Introduction to electrodynamics (Vol. 3). Upper Saddle River, NJ: prentice Hall.

Goal: 

Model the electric and magnetic fields (and D and H) of a solid toroidal conductor with a current flowing through it.  Originally, I intended to model the current as a volume current and vary the aspect ratio of the torus and determine the effects on the fields, but my preliminary research has shown that it is more accurate to model the current as several helically wrapped linear currents, similar to a toroidal solenoid.  I will vary the number of turns (N) and observe the effects of this change.  I will make my decision of initial values based on the values of current tokamak safety factors (safety factor, q{r), describes the ratio of the number of times a given magnetic field line wraps around the torus in the toroidal direction to the number of times it wraps around the torus in the poloidal direction).  Ideally, I will eventually model the tokamak as a series of concentric tori, since these linear helical currents exist throughout the volume of the plasma.  Initially, I will model it as one current along the outside of the plasma, surrounding a conductor

Tentative Methods:

• Determine the safety factor of, as well typical current through, a tokamak reactor, such as JET (the Joint European Torus).
• Using the above values, use Maxwell’s Equations to derive expressions for E and B of a torus (expanding upon Griffiths 3rd Ed. Example 5.10); expand this to account for D and H since the interior plasma can be magnetized.
• Consider how these quantities change as the safety factor of the torus is changed
• Use Mathematica to model these fields as N changes.

Resources:

• Griffiths Introduction to Electrodynamics, 3rd Edition
• Journal article (to be determined – for  JET specifications)

General Notes:

I think that the most difficult part of this will be in creating the model in Mathematica, and getting it to do what I want.  I feel relatively confident about the ease of determining the values to use, and about deriving expression for E and B, though those are not trivial calculations.  Once I have the expressions, it will be relatively simple to vary q(r).

 Schedule:

7 April – 13 April: Research tokamak properties and determine current and size values.  Begin work to derive expressions for B.  Update Project Plan to account for comments.

14 April – 20 April (Tuesday 15 April: Updated Project Plan): Check expressions for B, and then find other fields.  Begin work on building Mathematica model.

21 April – 27 April  (Tuesday  22 April: Preliminary Results): Work on fixing issues with the Mathematica model, and make sure that it works and looks as desired.  Draft conclusion/interpretation of results.  For results, have expressions for all necessary quantities and have a first draft of model.

28 April – 4 May (Thursday 1 May: Begin Presentations): Refine model, and fix any remaining issues.  Elaborate on interpretation of results.  Begin reviewing classmate’s project.