Alex Molina & Kadeem Nibbs
Computational Physics 375 – Final Project

Project Motivation

We wanted to model the Long Jump track & field event to see if we could mathematically incorporate technical elements to the simple projectile motion model and see tangible differences in jump distances.  We also wanted to model the effects of air, since we thought that wind speed and air density must have some effect on jump distances, but did not know how to quantify its impact.  We believed we could achieve these goals with a comprehensive Matlab program, and Chapter 2 of Giordano and Nakanishi’s Computational Physics on realistic projectile motion gave us a clear starting point.

Program Description

This program simulates the long jump track and field event to observe changes in jump distance as related variables are adjusted. The variables we were most interested in are: air density, to determine if jumps done at different altitudes are comparable; wind speed, to observe how much wind resistance can affect performance; whether or not the athlete cycles his or her arms in the air, to see how this movement affects body position in the air; and, of course, the final jump distance.  We could also adjust the size of our athlete using our program, but the adjustments, as long as they are kept within reasonable limits, would have a negligible effect on the results.  The athlete’s physical proportions are based off of our very own Kadeem Nibbs, who always wanted to participate in the long jump but never could due to scheduling conflicts.

We originally wanted to use 3D models to run all of our tests, but working with 3D shapes and deforming them proved difficult.  We decided to use point particles for the tests where they provide an accurate approximation (wind assistance and air density), and then 2D “patch” shapes for tests where body position became exceedingly important (limb cycling).  For the trial where the athlete did not cycle his limbs, we created one fixed-shape rectangle to model the athlete’s body, as if he were held rigid throughout the entire jump. We modeled the athlete with two rectangles when limb cycling was allowed, one rectangle to represent the torso, and another for the legs, so that they could move independently.

Final Results

Real World properties and their affect on Long Jumping:

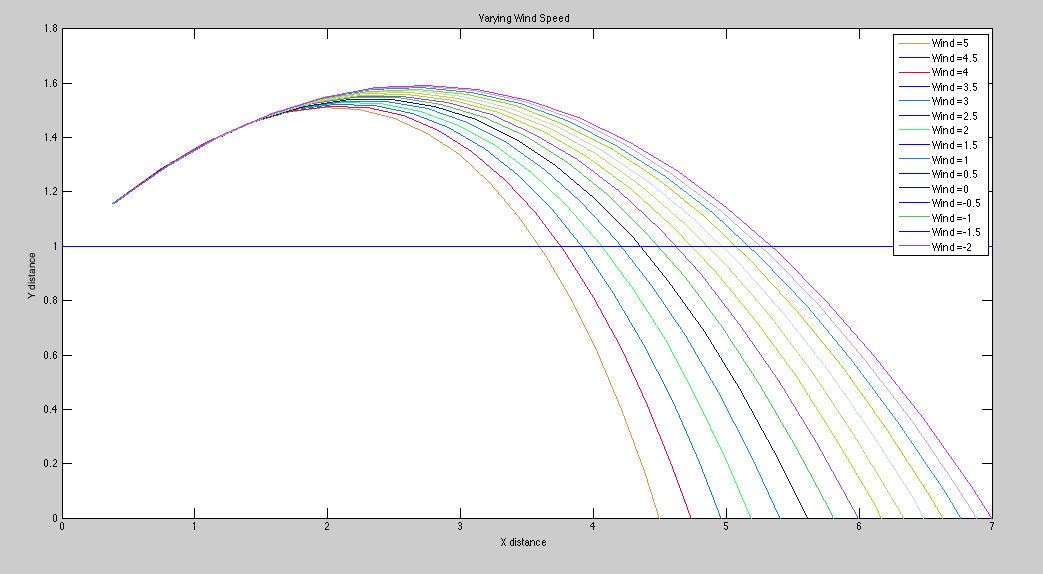
While our preliminary results showed that wind had a major impact on the final jump distance, with a difference of 7m/s resulting in a change of approximately 2 meters in jump distance, we found that this was due to a missing square root sign when calculating velocity.  When this was fixed, we found that the same difference in wind speed accounted for a difference in inches in jump distance.

Our Resulting Projectile Motion with Varying Wind Speed:

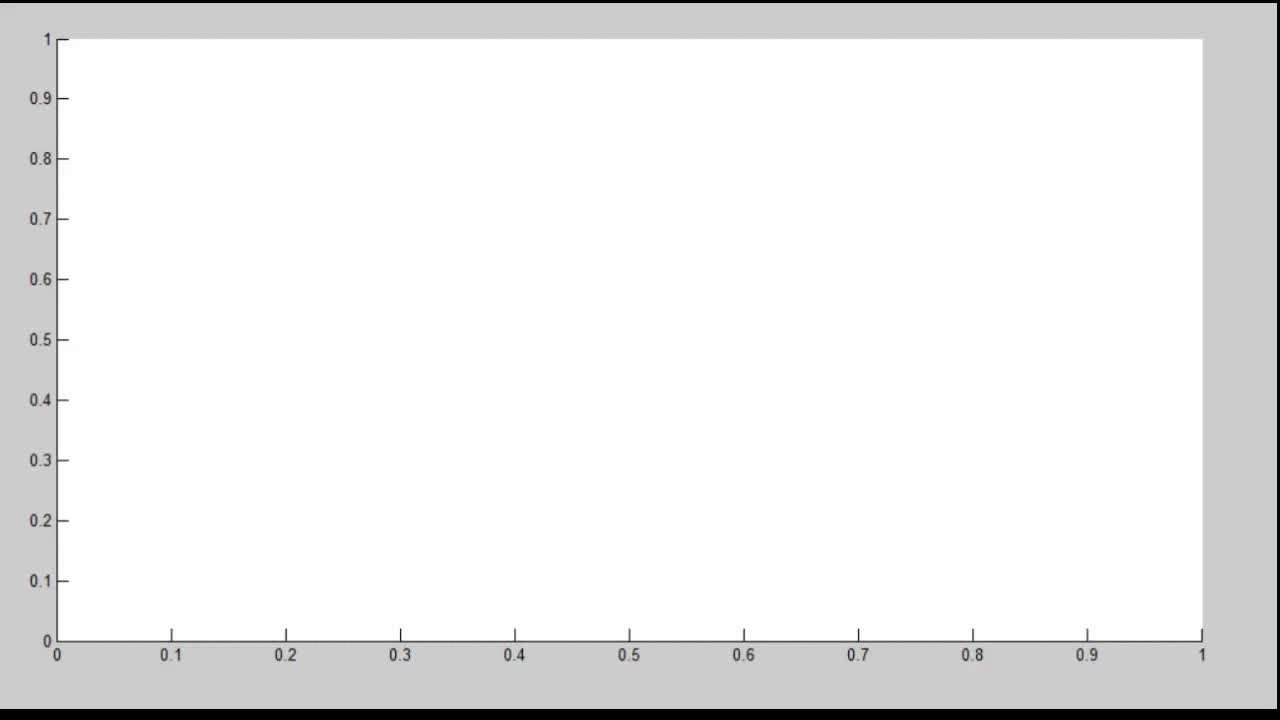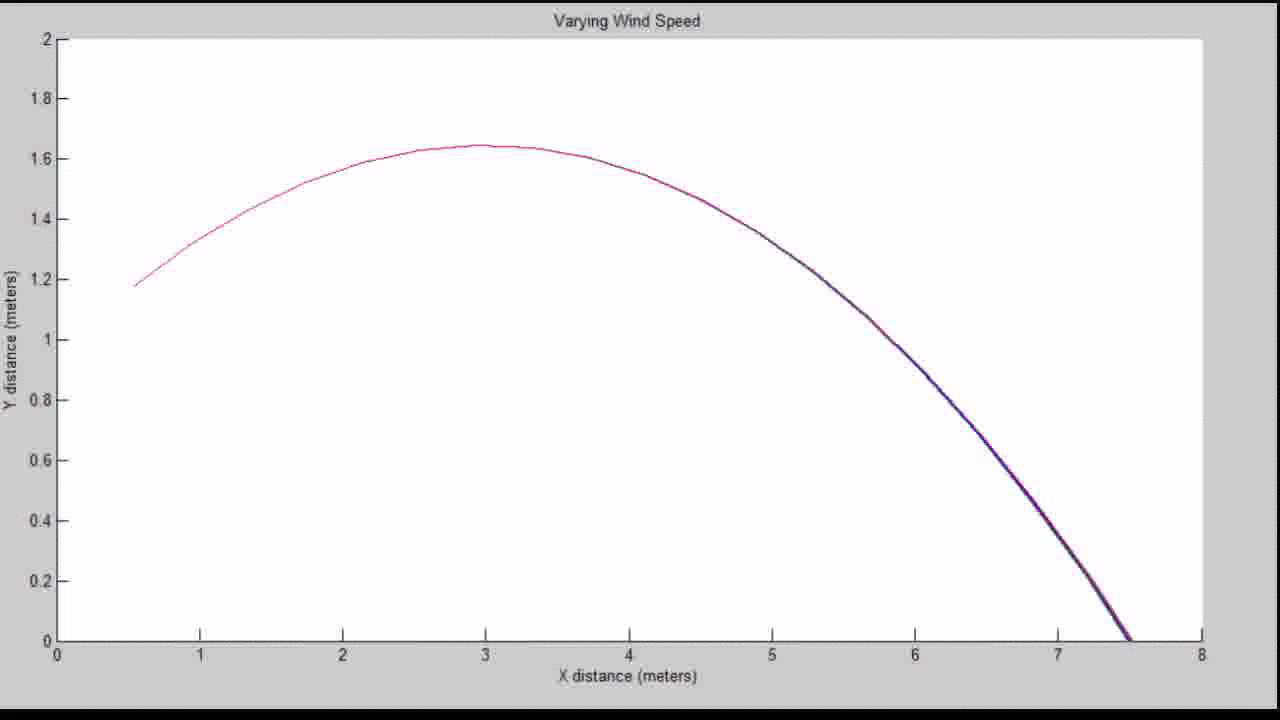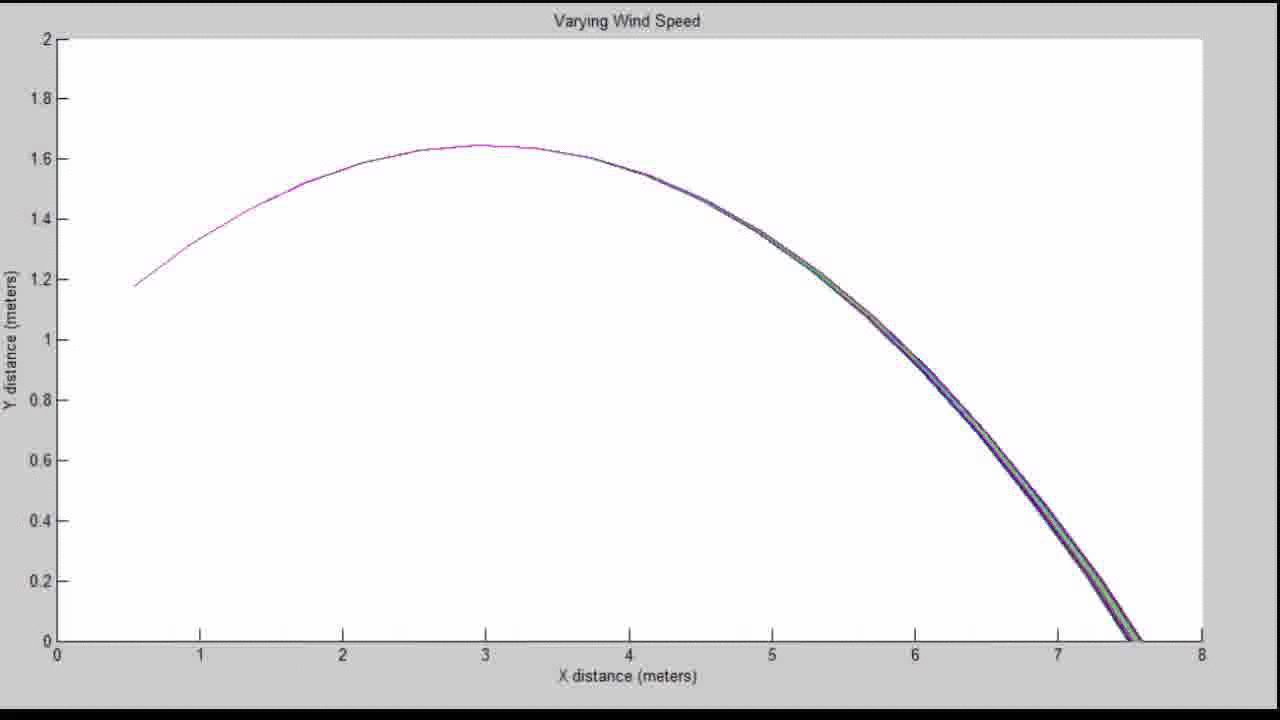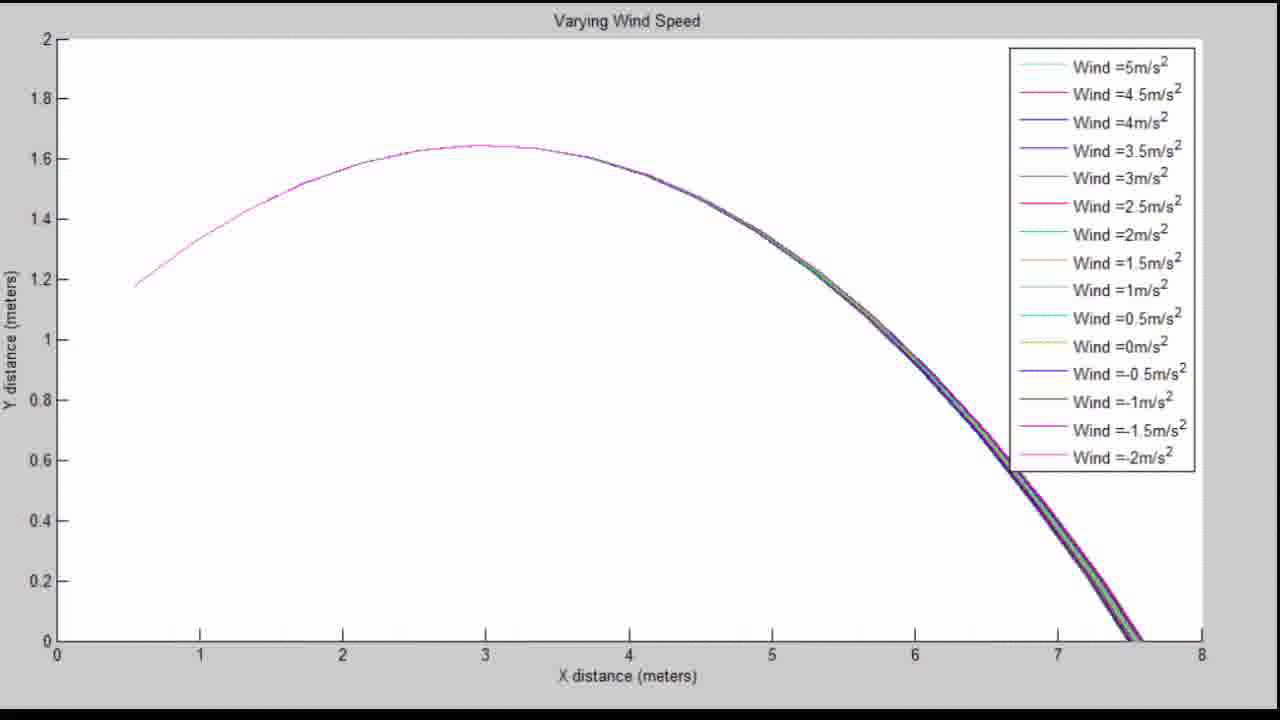
Our Resulting Projectile Motion with Varying Wind Speed (close up view):

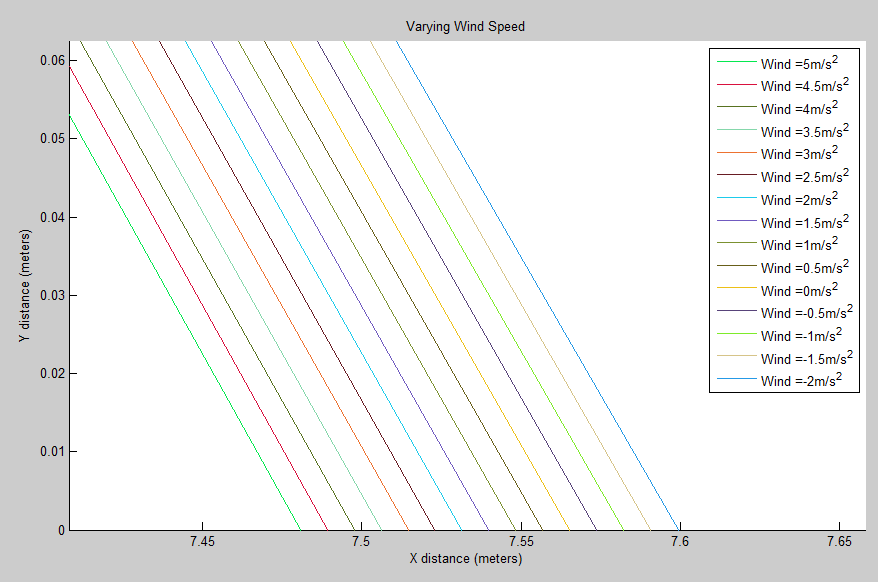
A 0.1 change in meters is about a difference of 4 inches. While this may seem negligible on a macroscopic level, the top two World Records in the long jump only differ by 4.5 inches.  So a fortuitous wind gust may be the difference between a gold medal and nothing.

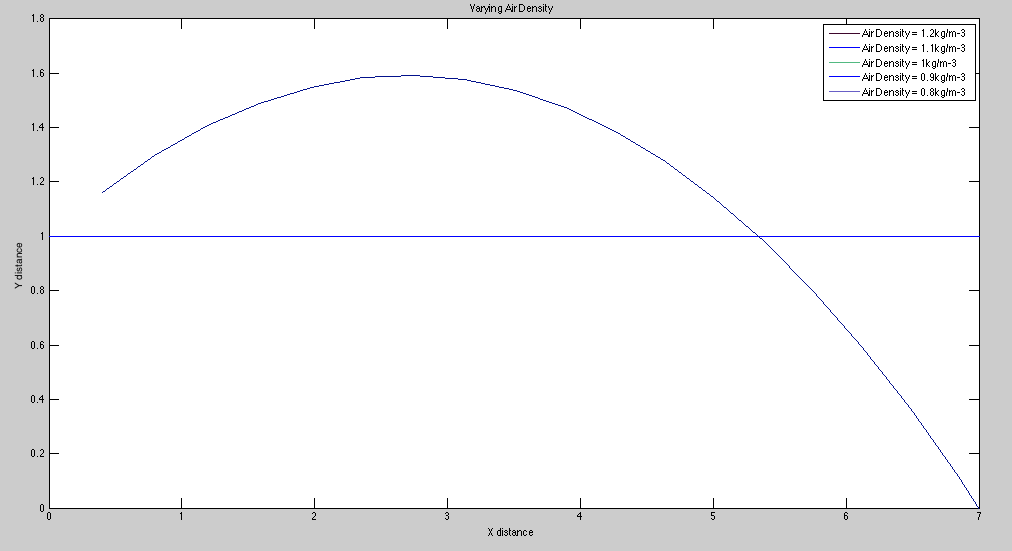
For our second real world property we found that air density had a negligible effect on the jump distance, as variations of up to 50% in air density resulted in less than a millimeter of difference. This reaffirms what was learned in introductory mechanics: that air resistance is negligible in most cases of projectile motion, with exceptions being when the air is moving and when the object is moving at high speeds.

Our Resulting Projectile Motion with Varying Air Density:

Air resistance will not significantly affect an athlete jumping at 20mph into still air. This also shows that although air density can be as high as 1.2kg/m^-3 at cities near sea level, and as low at .75kg/m^-3 at cities 5000m above sea level, long jumps performed at any city in the world can be compared because of air density’s negligible effects on performance.

Modeling the Human with the Patch Mechanism:

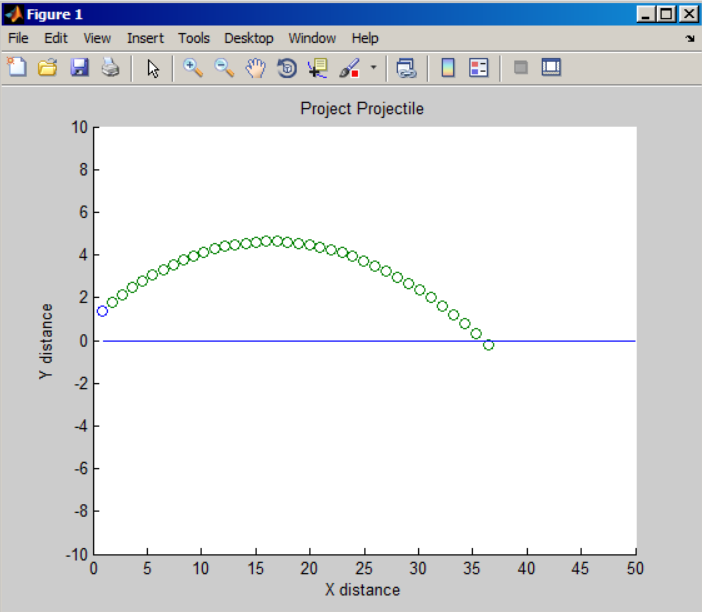
After thoroughly researching track and field coaching manuals and websites, we learned that the purpose of cycling one’s arms and legs while in the air is to keep one’s torso from rotating forward. The torque generated during an athlete’s takeoff typically generates a large forward angular momentum. As a result, if an athlete does not cycle their arms/legs properly while midair, they may end up tilting too far forward, hitting the ground face first, and losing some of their teeth. This is demonstrated in the figure below when our code is run.

Our Resulting Projectile Motion Modeling a Human without limb cycling (head diving):

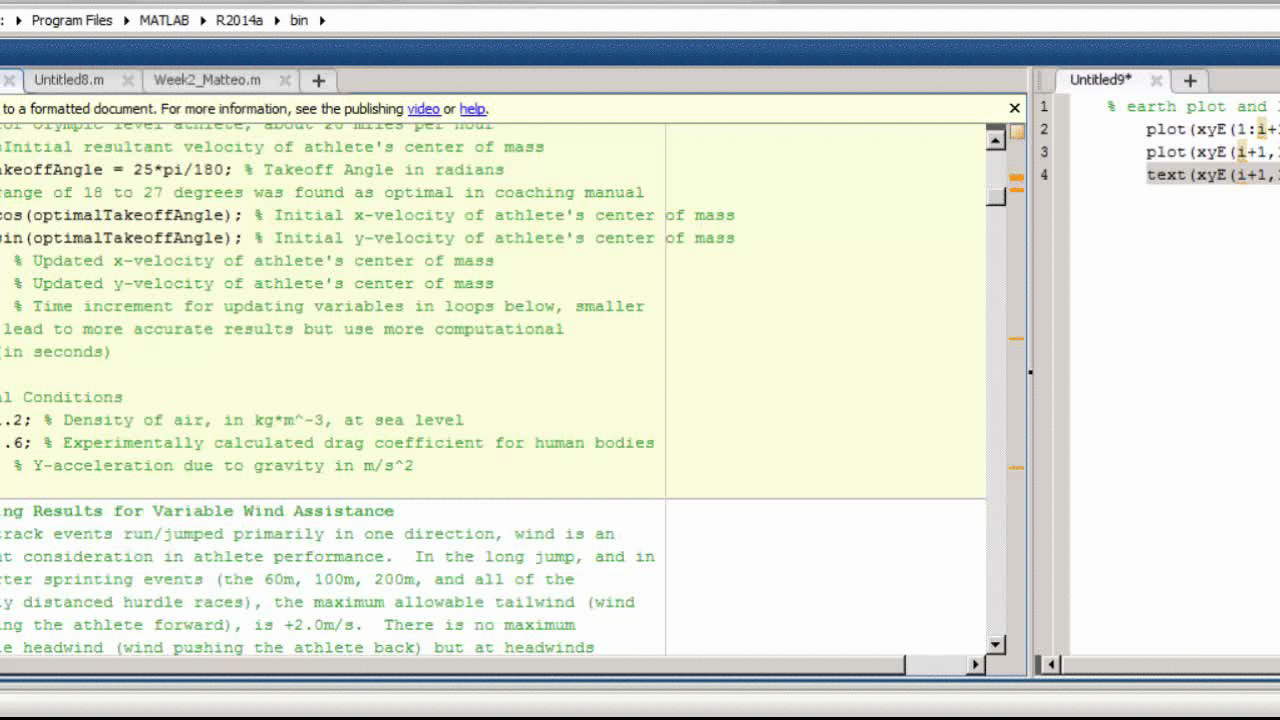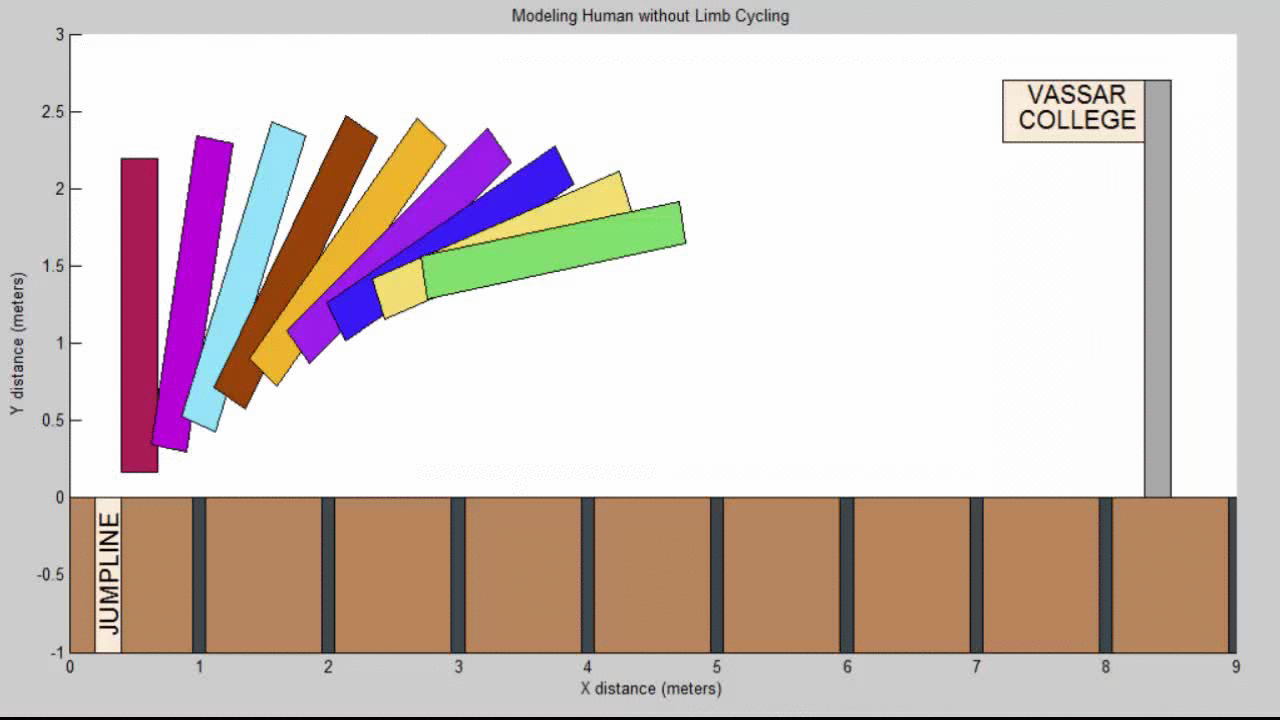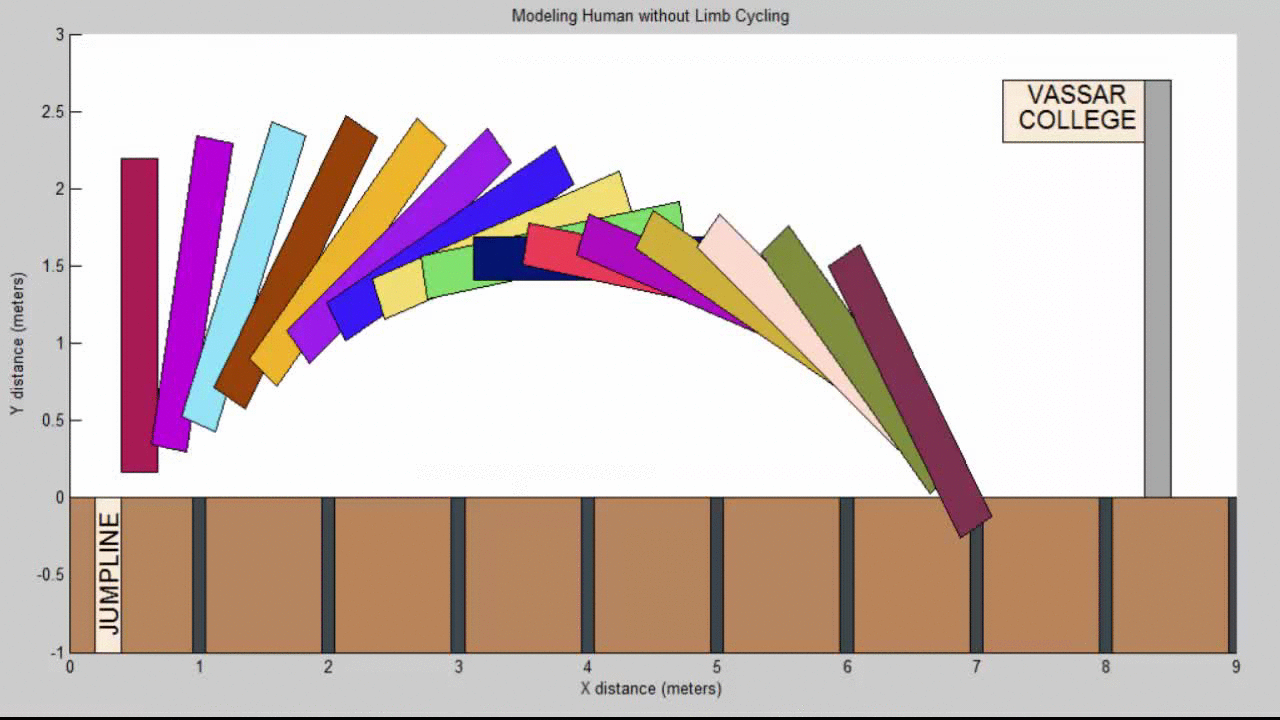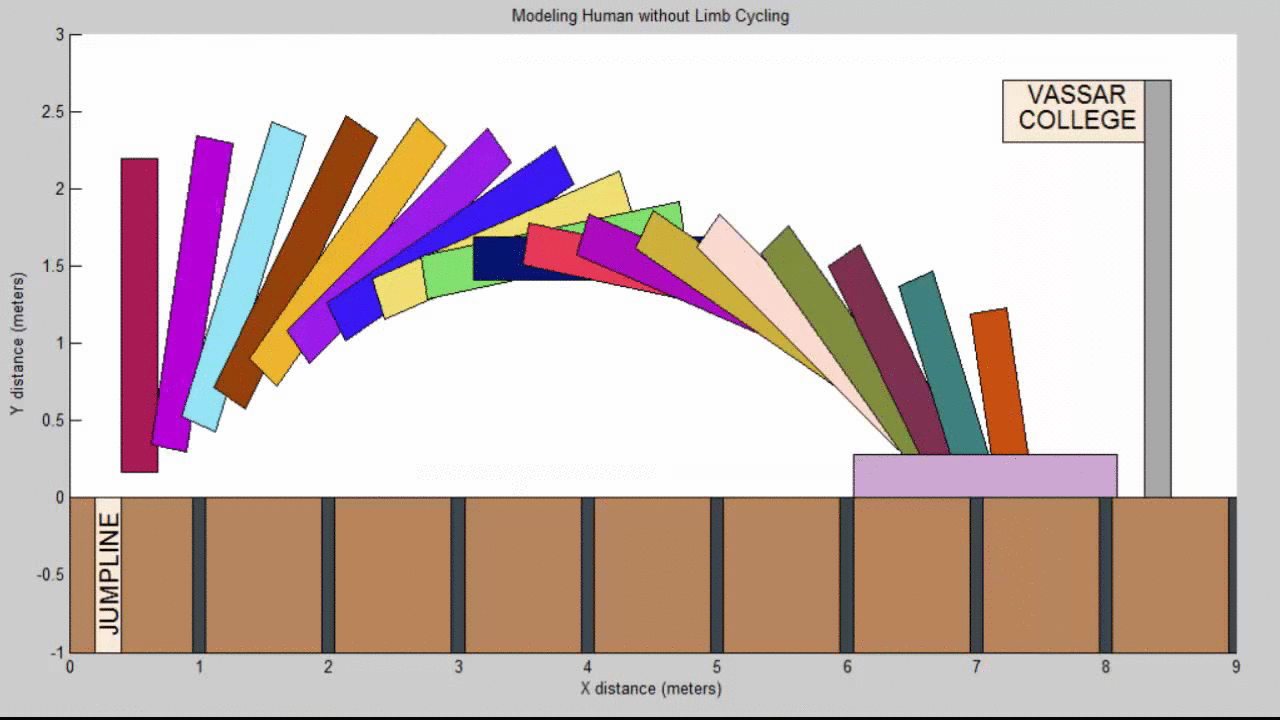
The forward angular momentum is especially detrimental because, if the torso is angled too far forward during the jump, the legs will inevitably end up far behind the body.  Since jump distance is recorded at the furthest back mark in the sand, if the athlete’s feet strike the ground a meter behind his center of mass, he is effectively disqualifying himself from competition.

By cycling his arms and legs, the athlete creates a forward angular momentum that is hopefully as large as that of his torso.  Since angular momentum is conserved for a projectile not subjected to any external torques, this generated angular momentum is subtracted from the torso’s angular momentum, allowing the athlete to stay upright.

Our Resulting Projectile Motion Modeling a Human while limb cycling:

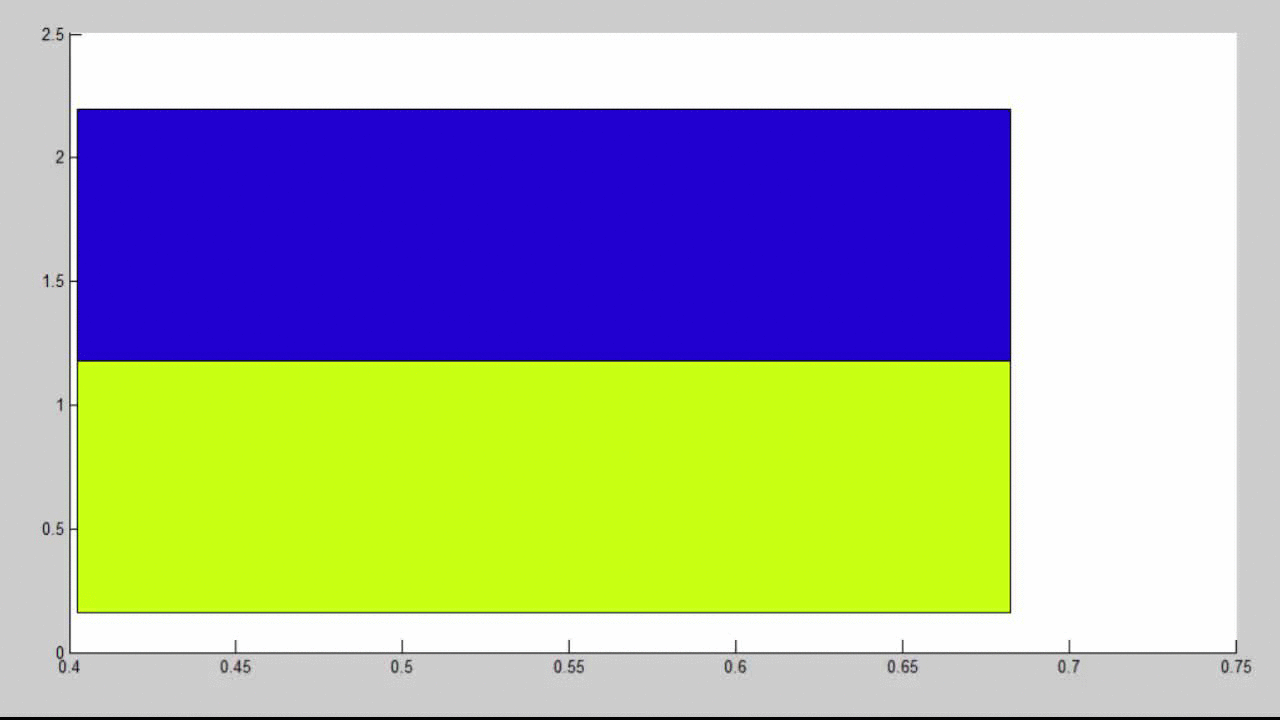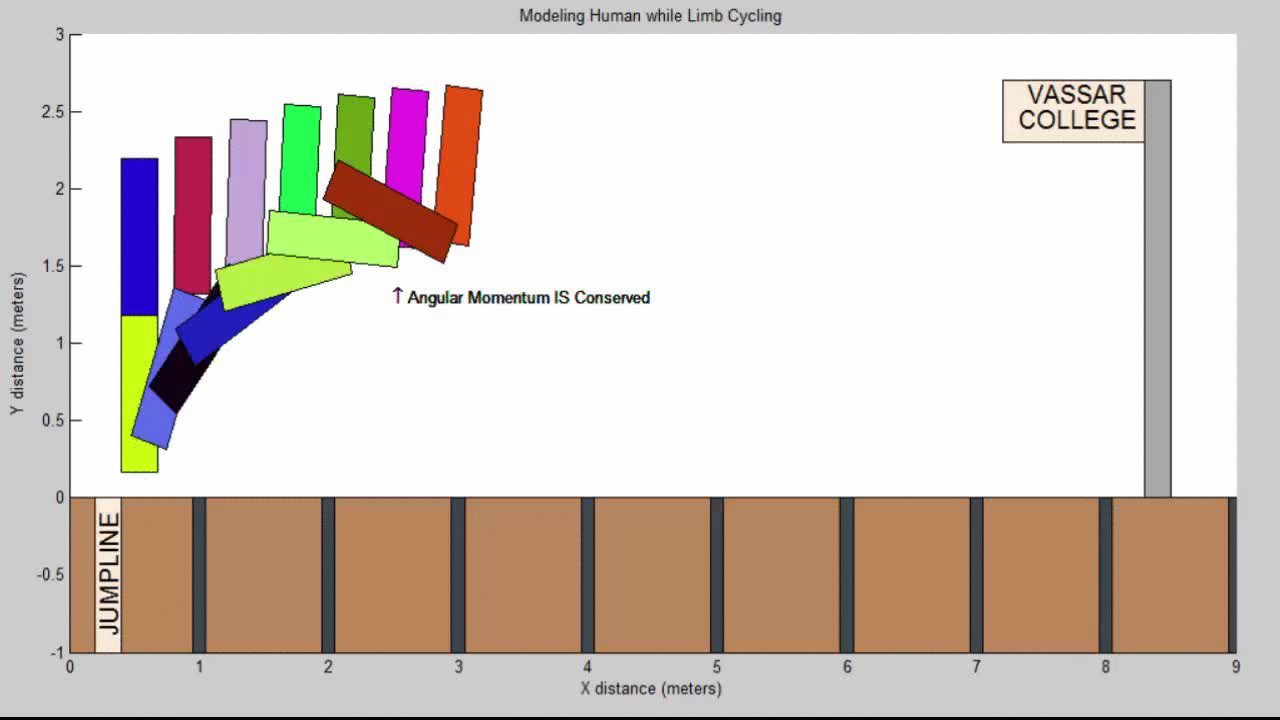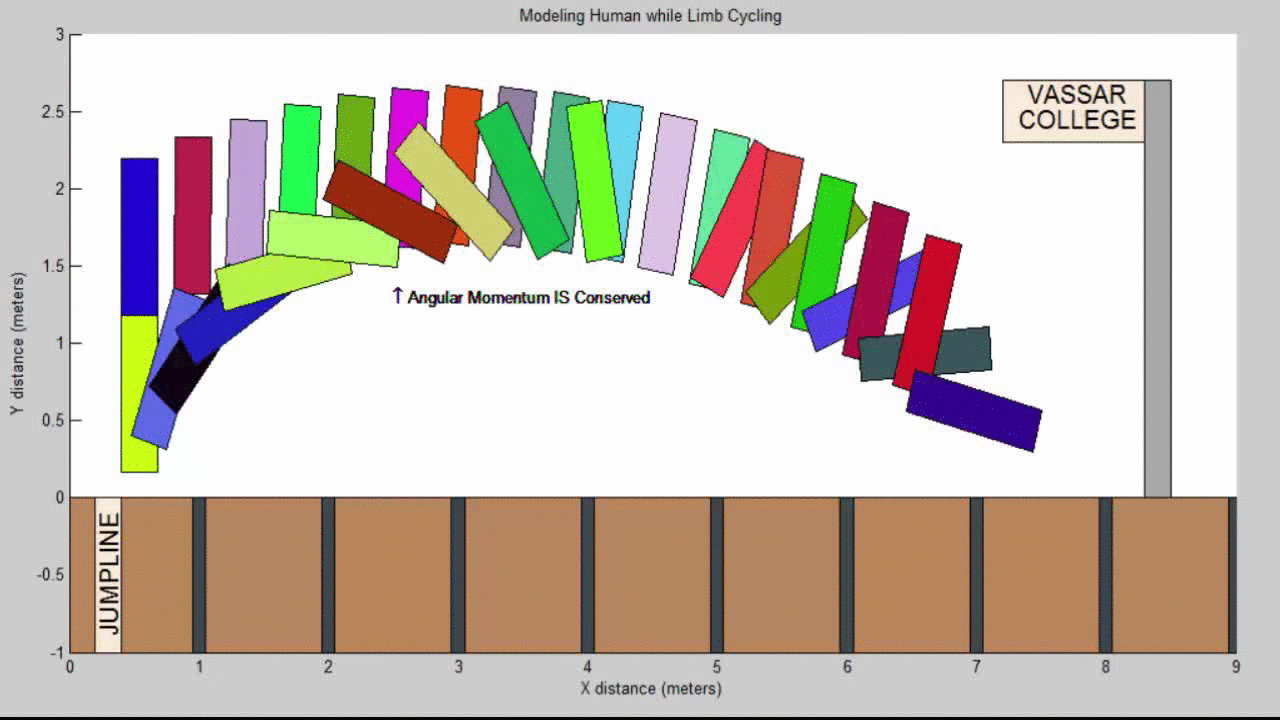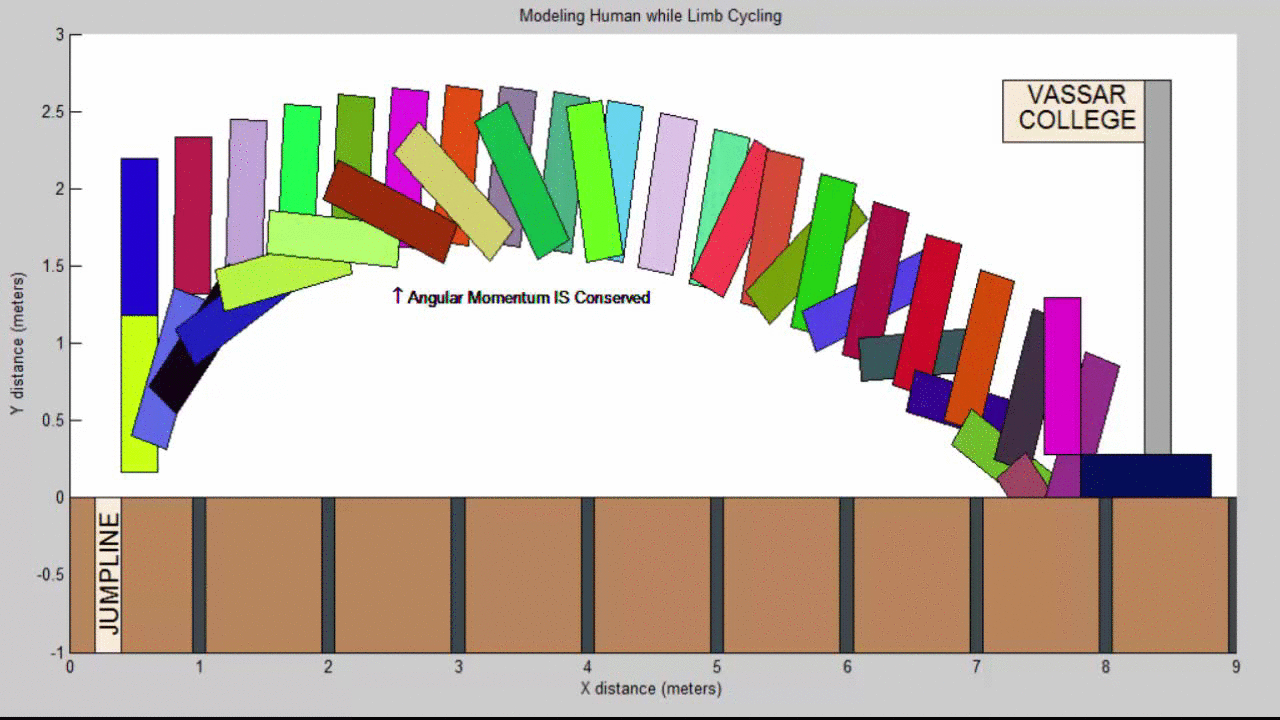
In this upright position, it is easy to tuck the legs in front of the body, so that the hips are the first to strike the ground.  With this change in technique, we noted a difference of approximately 1.5 meters in the final jump distance.

Future Goals and Endeavors:

Continuing with this work, we would like to get a more holistic model of the long jump, as the run preceding the takeoff, which we entirely ignored, is an essential part of the event.  We would like to see how the approach speed to the jump affects the optimal takeoff angle, and also incorporate arms and more realistic body proportions for our athlete. We believe that this project has a future where a variation of our code could be used by coaches and athletes to see what a human body’s characteristics must be in order to have the most efficient and longest jump. This could mean studying how a different weight, speed, height, cross sectional area, etc. could produce the “perfect conditions for jumping the longest.”

Overall, we were able to model a human figure using the patch mechanism and we were very satisfied with this result. We were able to work together on close to 400 lines of difficult computational code and our knowledge of physical and computational concepts has since grown. We see now how realistic models can be designed on MatLAB and through this, they could be studied to see how different human characteristics could affect a long jumpers distance, whether it be a few millimeters to a few inches.

Our Final Computational Codes: 

Our final MatLAB code with and without the added patch motions are uploaded on this drive (just click the image below). Note that all the codes are listed in a text file (such as Notepad for Windows).  They will have to be manually copied into a script function in the Matlab program. This is due to the fact that we used a Citrix XenApp that allowed us to run MatLAB on our computers but not be able to save the files onto our own desktop.

References:

Knight, Randall Dewey. “Rotation of a Rigid Body.” Physics for Scientists and Engineers: A Strategic Approach. 3rd ed. Boston, Mass.: Addison-Wesley, 2012. 312-387. Print.

Giordano, Nicholas J., and Hisao Nakanishi. “Chapter 2: Realistic Projectile Motion.” Computational Physics. 2nd ed. Upper Saddle River, NJ: Pearson/Prentice Hall, 2006. Print.

MATLAB R2014b by MathWorks®

Acknowledgements:

We would like to thank Vassar College for allowing us to use their 24/7 Physics department computer room to help complete our project.  We would also like to thank our peers for giving us feedback on how we could expand on our project and helping us with fixing some minor computer codes. And a final thank you to Professor Magnes for teaching us the essential basics to coding and for guiding our project to what it is today. It has been a wonderful semester and we know that we will use our computational knowledge to further our intellect as physicists.

Alex Molina & Kadeem Nibbs
Computational 375 – Project

GOAL: Week 2: Run simple trial with one-dimensional object in two-dimensional space with air resistance ( varying wind speeds and air densities)

In all track events run/jumped primarily in one direction, wind is an important consideration in athletic performance. In the long jump, and in the shorter sprinting events (the 60m, 100m, 200m, and all of the similarly distanced hurdle races), the maximum allowable tailwind (wind propelling the athlete forward), is +2.0m/s. There is no maximum allowable headwind (wind pushing the athlete back), but at headwinds stronger than -5.0m/s, an event might be postponed. For our latest results presentation, we compared the jump trajectories while varying wind assistance and air density, in each case holding all other variables constant.

Our original goal for the week was to improve our model to have a 3D projectile with limb objects, functions to bend and extend the limbs, and methods to calculate the cross-sectional area and center of the mass of the body depending on the state of the limbs. However, we could not figure out how to implement object-oriented design in MatLab, and we failed to properly define functions in our code, which made our prospects shaky at best. We instead decided to learn what information we could from our current working model.

Our results showed that wind assistance has a major impact on performance in the long jump, as a jump into a 5m/s headwind netted a distance of about 5 meters, a mediocre distance for a male high school jumper, and a jump propelled by a 2m/s tail wind recorded a distance of nearly 25 feet, which is an elite college-level distance. We found that air density had a negligible effect on the jump distance, variations of up to 50% in air density resulted in less than a millimeter difference. This reaffirms what we learned in introductory mechanics, that air resistance is negligible in most cases of projecting motion, the exceptions being when the air is moving, and when the object is moving at high speeds. Air resistance will not significantly affect an athlete jumping at 20mph into still air. This also shows that although air density can be as high as 1.2kg/m^-3 at cities near sea level, and as low at .75kg/m^-3 at cities 5000m above sea level, long jumps performed at any city in the world can be compared because of air density’s negligible effects on performance.

Important Links:
MatLAB code and other essential information can be found at:
https://drive.google.com/open?id=0B6loGd4o7iESfjNoRnVmSjJDNHlabG9qNEJIRmY1Z1JEeS1QNE9rTjlIY2Vqc1NMTWlwdEk&authuser=0

References:
Giordano, Nicholas J., and Hisao Nakanishi. “Chapter 2: Realistic Projectile Motion.” Computational Physics. 2nd ed. Upper Saddle River, NJ: Pearson/Prentice Hall, 2006. Print.

Our Resulting Projectile Motion with Varying Wind Speed:

Our Resulting Projectile Motion with Varying Air Density:

UPCOMING: Week 3: 
Run a second trial with a mass-less two dimensional object in 3-dimensional space. We will more to run two test trials with three-dimensional object in three-dimensional space, each with different body position.

Alex Molina & Kadeem Nibbs
Computational 375 – Project

GOAL: Week 1: The setup. Establishing the arrays, the initial variables and conditions.

This week we worked on modeling the long jump via MATLAB since we are interested in exploring realistic projectile motion and human acceleration as it pertains to the human body. For this week, we looked to create a baseline code modeling a point particle with air resistance(drag force) and gravity acting on it.

We want to explore the effects of proper body position on the traveled distance in the long jump, so modeling after Chapter 2: Projectile Motion, we worked to generate a realistic curving point through Earth’s atmosphere. Our goal to set a baseline is complete. For the upcoming weeks, we will work to add air resistance and friction in effect. To make the point particle even more interesting, we will start to add cylindrical and spherical shapes in order to resemble a more humanistic body and interesting projectile.

Important Equations:
Drag Force of Air:
Drag Force of Air in the x direction with the x component of velocity
Drag Force of Air in the y direction with the x component of velocity
Important Links:
MatLAB code and other essential information can be found at:
https://drive.google.com/a/vassar.edu/folderview?id=0B6loGd4o7iESfjNoRnVmSjJDNHlabG9qNEJIRmY1Z1JEeS1QNE9rTjlIY2Vqc1NMTWlwdEk&usp=sharing

References:
Giordano, Nicholas J., and Hisao Nakanishi. “Chapter 2: Realistic Projectile Motion.” Computational Physics. 2nd ed. Upper Saddle River, NJ: Pearson/Prentice Hall, 2006. Print.

Our Resulting Projectile Motion via MatLAB (GIF):
We saved the 40 different jpg files from MatLAB and used a gif generator to make this.  It did however erase the line and motion at each point.

Our Resulting Projectile Motion via MatLAB (Actual):

UPCOMING: Week 2: Run simple trial with one-dimensional object in two-dimensional space with air resistance.  Then second trial with a mass-less two dimensional object in 3-dimensional space.

1. Introduction

The human body is an elastic and versatile model.  It can move muscles individually or in a systematic way in an instant. For our project, we are interested in exploring realistic projectile motion and human acceleration as it pertains to the human body.  While we often assume air resistance and spin to be negligible in Introductory Mechanics, as a way of simplifying our calculations, it is impossible to ignore their effects in competitive events like the long jump.  The additional drag force caused by a single misplaced limb can lead to a loss of centimeters on a jump.  This difference may indeed be negligible in the context of an Introductory Mechanics problem, but is everything to an athlete competing for medals and sponsorship.  For our project, we want to explore the effects of proper body position on the traveled distance in the long jump, in addition to exploring the negative effects of improper position.

2. Project Details

In order to do this, we believe we will need to devise a way of modeling the human body as a 3-dimensional object inside a larger 3-dimensional array representing space.  If we find it necessary later on, we can make the body as low profile as possible by modeling it as a stick figure.  We intend to impart initial conditions onto the object using the “Previous, Current, Next” template we have been using in our homework, to give the body an initial x and y velocity.  The experimentation will occur in the middle of the jump, where we will change the position of various limbs of the body (possibly through matrix multiplication, as is done in computer animation), and compare the results on the final jump distance.  Changing body position will both change the surface area profile of the body, changing the drag force, and change the body’s center of mass which may lead to spin in the face of wind.  We will draw examples of proper and improper form from the literature produced by top track and field coaches so that our program will be grounded in reality and have some practical value.

2. Motivation for Project

Track and Field and athletics in general have been major parts of both of our lives as, between the two of us, we have participated in basketball, volleyball, cross country, track and field, and swimming at a Varsity level.  Also, both of us have considered careers in the Health & Fitness Industry in the past, and are still interested in ongoing developments in the field. We are both interested in the underlying mechanisms that go into making the simplest, and most human tasks, such as walking, running, and jumping, as efficient as possible.  We also both competitive people and have spent years fussing over minute details to give us the smallest competitive advantage.  We are excited to see what we can accomplish now with our improved knowledge of physics and the powerful software at our disposal.

References (will add more at a later time)

Giordano, Nicholas J., and Hisao Nakanishi. “Chapter 2: Realistic Projectile Motion.” Computational Physics. 2nd ed. Upper Saddle River, NJ: Pearson/Prentice Hall, 2006. Print.

Kinematic Equations

Projectile/Range Equations

Timeline (subject to change depending on our work efficiency):

Week 1: The setup. Establishing the arrays, the initial variables and conditions.

Week 2: Run simple trial with one-dimensional object in two-dimensional space with air resistance.  Then second trial with a mass-less two dimensional object in 3-dimensional space.

Week 3: Two test trials with three-dimensional object in three-dimensional space, each with different body position.

Week 4: All trials complete, finalizing the written report and conclusion.

For our project, we are interested in exploring realistic projectile motion as it pertains to the human body.  While air resistance and spin often produce negligible effects for the objects in introductory mechanics, normally modeled as point particles, they can produce significant effects on objects with larger surface area and mass, such as the human body.

In addition to this, with athletic competitions often being decided by seconds in races or mere inches in jumping events, minimizing adverse effects can ensure victory.  We are interested in modeling the human body in motion in MatLAB in Olympic jumping events, contorting limbs in obscure positions and seeing how it affects the ultimate outcome of the event.