Interpreting a H-NMR Spectrum | Modeling and Experimental Tools with Prof. Magnes

The NMR Spectrometer at Vassar college is graded at 300 MHz. This means the Larmor frequency of a single, unaltered hydrogen nucleus and its electron with $\sigma=0$ , is 300 MHz. The magnetogyric ratio $\gamma$ of a hydrogen nucleus is 267.513 $*10^{6}\frac{rad}{T•s}$ . A quick calculation using:

(1) $\begin{equation*} \nu_{0}=\frac{\gamma B_{0}(1-\sigma)}{2\pi} \end{equation*}$

shows the magnetic field strength of the NMR is roughly 7.046 T.

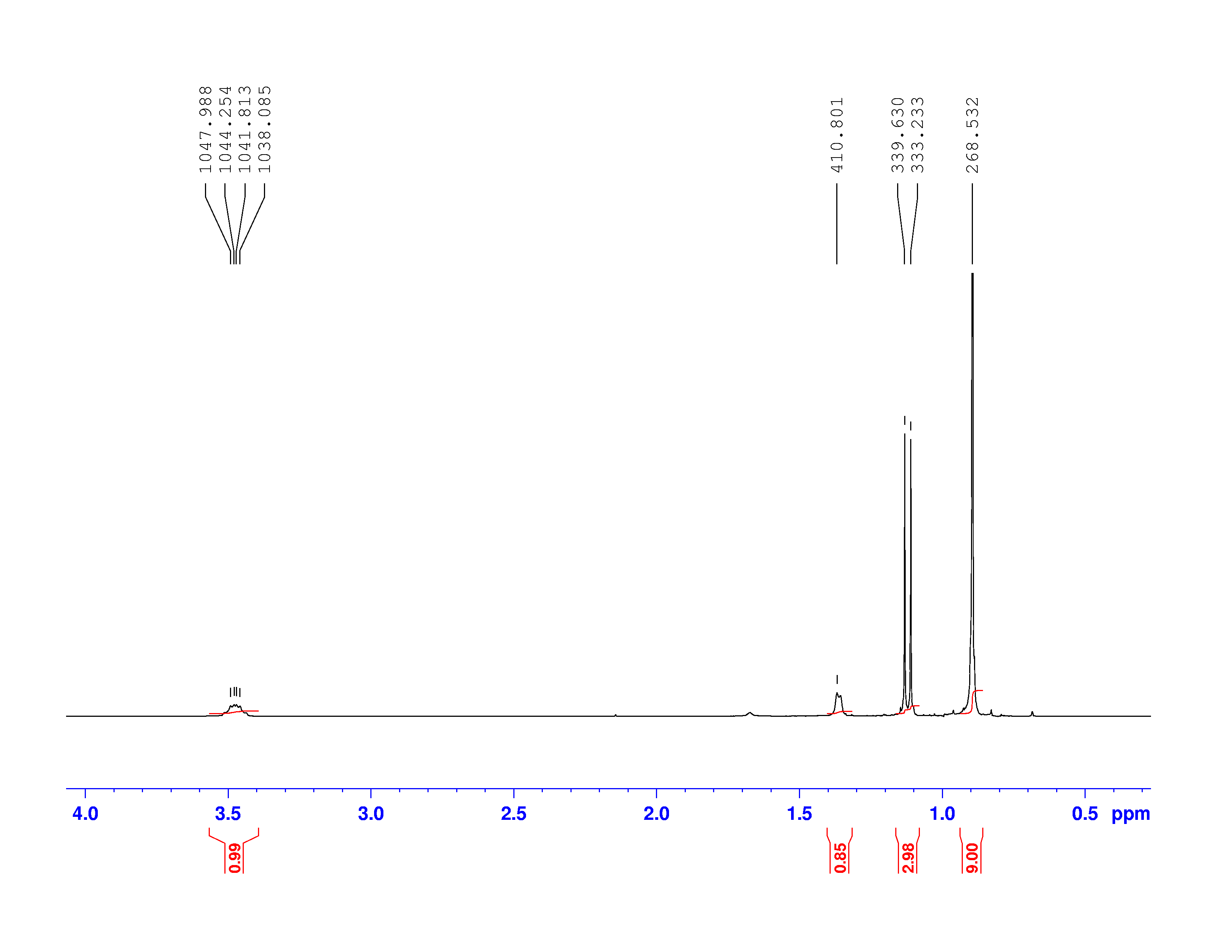
Using this information and the $^{1}$ H-NMR spectrum, we can calculate shielding factors for each type of hydrogen nucleus in 3,3-dimethyl-2-butanol, and determine what each spectrum peak actually means.

Let’s start with the peak farthest to the right on the spectrum. It is a single peak, called a singlet, that represents nine hydrogens, and is centered at approximately 0.9 ppm on the x-axis. The ppm scale measures how much the Larmor frequency of hydrogen is changed by the effective magnetic field. The Larmor frequency of the hydrogens represented by the first peak was increased by 0.9 ppm of the initial 300 MHz frequency. A calculation of these hydrogens’ shielding factor follows using equation (1):

$300 MHz+(\frac{0.9 ppm}{10^{6}}*300 MHz)=\frac{267.513*10^{6}\frac{rad}{T•s}*7.046T*(1-\sigma)}{2\pi}$

$300000270 Hz=299990611 Hz(1-\sigma)$

$\sigma=-3.2198*10^{-5}$

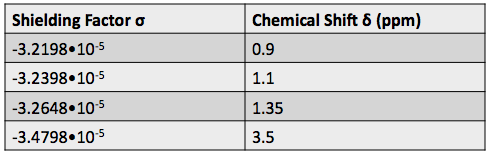
Shielding factors tend to be small for most hydrogen nuclei. A table of chemical shift and shielding factor values for each hydrogen nucleus in 3,3-dimethyl-2-butanol is below.

A more negative shielding factor corresponds with a lower electron density around the hydrogen nucleus and with a larger effective magnetic field influencing the nucleus. The presence of very electronegative atoms, like oxygen, near the hydrogen causes increased chemical shifts like the 3.5 ppm shift in the table.

One peak in the spectrum above is split into two peaks centered around the chemical shift 1.1 ppm. This splitting occurs because there is another magnetically active hydrogen nucleus nearby in the molecule. The rule for split peaks is: the number of nearby hydrogens is given by $n-1$ , where $n$ is the number of peaks. The definition of “nearby” is usually 1 carbon atom over in the molecule from the one the original hydrogen is attached to.

The figure below shows the structure of 3,3-dimethyl-2-butanol with the hydrogens labeled with their corresponding chemical shifts. This will be the first step in reconstructing the molecule from the NMR data.