An acoustic plane wave is defined much as you’d expect: as a “plane” of sound energy traversing a medium. When this wave encounters an object, there are several possibile outcomes:
1) Diffraction–the sound is “bent” around the object and its path is therefore altered;
2) Scattering–the sound is reflected off of the object and its path is thus altered;
3) Refraction–the sound passes through the object and its path is therefore altered due to a change in medium.
In this project I shall consider only diffraction and scattering, as the “object” I have chosen is a perfectly rigid, acoustically non-transparent sphere (i.e. sound cannot pass through it). In practice, it is seen that diffraction occurs for high wavelength (low frequency) sound only, and as frequency increases, scattering becomes the dominant phenomenon.
Like any wave, there is a wave equation dictating the propagation of an acoustic wave. Its solution is, however, quite complicated (especially in the presence of objects/barriers), and although analytical solutions exist for diffraction and scattering on a sphere, its components, which require complex functions such as Spherical Bessel and Hankel functions and their derivatives, whose values cannot be precisely (analytically) determined using computational methods, and which therefore must be approximated much like we approximated the solutions to differential equations using the Euler, Runge-Kutta, or similar methods.
For the sake of illustration the acoustic wave equation in three dimensions is:
Notice that this is a 2nd order differential equation the likes of which we have handled in class.
The layout of the project is this (in order of importance):
1) to use the acoustic wave equation to numerically solve the problem of diffraction (low frequencies) and scattering (high frequencies) of the wave on the surface of a rigid sphere;
2) to compare this result to the analytical results available;
3) to provide a visual or graphical representation of the phenomena;
4) to discuss error propagation in numerical method and the method by which the Spherical Bessel and Hankel functions described earlier are approximated;
5) to, if possible, discuss the spherical harmonic decomposition of sound on the surface of the sphere, which provides a rigorous basis for accurately modeling the sound up to a certain frequency.
This last point also requires the evaluation of integrals (in a way analogous to that of Fourier Transforms in 2D), which by the nature of computation are impossible to solve perfectly using numerical methods, but must be approximated as sums. If I am able to include this last point, I will also discuss the method of approximating the integrals.
Timeline:
Week 1: Research into necessary equations and computational methods, begin code for calculation of diffraction and scattering.
Week 2: Continue code to the point of having a visual/graphical representation (hopefully!)
Week 3: Compare results to analytical results, if enough time work on spherical harmonic decomposition of sound field on surface of the sphere.
Week 4: Presentation and write-up.
Sources:
Computational Physics, Giordano and Nakanishi, Chapter 6.
O’Donovan et al. REAL TIME CAPTURE OF AUDIO IMAGES AND THEIR USE WITH VIDEO. 2007.
Li, et al. A ROBUST AND SELF-RECONFIGURABLE DESIGN OF SPHERICAL MICROPHONE
ARRAY FOR MULTI-RESOLUTION BEAMFORMING. 2005.
And certainly others to be found along the way.

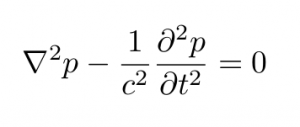

I’m mostly interested in the near field effects, since I’d like to understand the sound field on the surface of the sphere (or almost on the surface).
– Nice explanation of scattering, diffraction and refraction.
– Are you looking at near or far-field effects?