Thus far, I have determined values for the quantities of interest (except for $\mu$ of the plasma) and I have derived an expression for B and H. I will base the parameters of my model off of the Joint European Torus (as per Albanese, et al., 03; Crisanti, et al., 03). It appears that there will be no D field, since the plasma is a conductor and would not polarize, but simply experience a current.
- $q(r) = \frac{r B_{\phi}(r)}{R B_{\theta}(r)} = 3$
- $r = .95~m$
- $R = 2.85~m$
- $I = 6.0~MA$
I am going to assume that N, the total number of turns, is proportional to the safety factor: $N = \alpha q(r)$ where $\alpha$ will probably be related to the circumference of the torus (which can be found from the radii).
The Biot-Savart Law gives:
$d\textbf{B} = \frac{\mu_{0} \textbf{I} \times \textbf{r} dl}{4 \pi r^{3}}$.
If we assume that the torus is in the x-y plane, centered at the origin, and consider a test point at $\textbf{r}$ and source charge elements at various $\textbf{r’}$. Then $\scriptr = \textbf{r} – \textbf{r’}$. Consider a test point on the x-z plane.
Assuming that the winding is tight enough, we can say that $ \textbf{I} = I_{s} \hat{s} + I_{z} \hat{z}$ which, in cylindrical coordinates, is $(I_{s}cos(\phi), I_{s}sin(\phi), I_{z})$.
In evaluating the Biot-Savart Law, we have the term $\textbf{I} \times \textbf{r}$. Due to the symmetry of the tours, the x and z components cancel out, leaving just a y component. If the test point is in the x-z plane, this means that the magnetic field will be circumferential, or in the positive $\hat{\phi}$ direction. The magnetic field can then easily be found using Ampere’s Law:
$\textbf{B(r)} = \frac{\mu_{0} N I}{2 \pi s} \hat{\phi}$
for all points within the minor radius (inside the torus) and
$\textbf{B(r)} = 0$
for all points outside the torus.
From here, it is also easy to find the Auxiliary field, from $\textbf{H} = (1/\mu) \textbf{B}$, so
$\textbf{H} = \frac{1}{\mu} \frac{\mu_{0} N I}{2 \pi s} \hat{\phi}$
inside the torus and
$\textbf{H} = 0$
outside the torus, since there is no magnetic field.
I have also begun work on my Mathematica model. I began by trying to figure out how to get the vector field to look right, and have been working with a simplified version of my B equation, $\textbf{B} = k/r$. I have found that the transform to spherical coordinates is easiest to work with (since toroidal geometries do not fit easily into either spherical or cylindrical), which is why my expression uses r instead of s. This has given the following vector field:
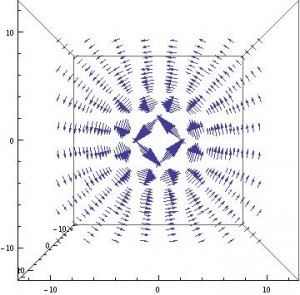
The (simplified) circumferential magnetic field due to a toroidal solenoid (without taking into account the fact that the field is zero outside of the loop of the solenoid).
The vector field is the shape that I need it to be, but I’m having some trouble getting the field to be zero outside of the solenoid. I tried to use the piecewise function of Mathematica, but keep getting an error. I think I may need to define two fields (maybe 3) such that they cancel out in the regions where the field should be zero.
The next step will be to input the numbers into my expression, and work out the Mathematica model. Then I will be able to easily vary q(r) and observe the results.
Link to Mathematica notebook: https://drive.google.com/file/d/0B-C9MvBAfmyIQS12dTZJOGh5bm8/edit?usp=sharing
References
Raffaele Albanese, G Calabr`o, M Mattei, and F Villone. Plasma response models
for current, shape and position control in jet. Fusion engineering and design,
66:715–718, 2003.
F Crisanti, R Albanese, G Ambrosino, M Ariola, J Lister, M Mattei, F Milani,
A Pironti, F Sartori, and F Villone. Upgrade of the present jet shape and vertical
stability controller. Fusion engineering and design, 66:803–807, 2003.
Griffiths, D. J., & Reed College. (1999). Introduction to electrodynamics (Vol. 3). Upper Saddle River, NJ: prentice Hall.


Be sure to include comments in your script so that your work can be followed easily. Part of your script is not working.