Considering the lifting magnetic force on the train’s superconducting coils, we know that at extremely low speeds, the magnetic force of repulsion will likely not be great enough to levitate the train. However, as the speed of the train increases, the lifting force should increase proportionally, as the magnetic repulsion force increases. It would be nice to have a compact equation directly relating the speed of the train to the lifting force; regrettably, I could not discover any such equation. There is, however, a method by which one can estimate this force. Just as there was the “Method of Images” to solve problems with conducting planes in electrostatics, there is a similar method for moving sources of magnetic fields. As the superconducting coils on the train pass over the conducting coils in the track, the repulsive force generated by the opposing magnetic fields between the two loops can be thought of as an equal and opposite force being created by an image of the superconducting coil located an equal distance away on the opposite side of (underneath) the track. Then, as the train moves forward some distance, a new image is created underneath the track, and the previous image begins to move away from the track, further into the ground. The speed at which the images recede from the plane is given by ![]() , where
, where ![]() is the permeability of free space,
is the permeability of free space, ![]() is the conductivity of the conducting plate (coils) in the track, and
is the conductivity of the conducting plate (coils) in the track, and ![]() is the thickness of the conducting plate. Though most of the force created by the images is repulsive, there is still the electromagnetic drag force created by the remaining currents in the passed loops, which can be thought of as coming from the previous images. This successive line of images is known as the “wake of images.”
is the thickness of the conducting plate. Though most of the force created by the images is repulsive, there is still the electromagnetic drag force created by the remaining currents in the passed loops, which can be thought of as coming from the previous images. This successive line of images is known as the “wake of images.”
Figure 2. The “wake of images” that appears on the opposite side of a conducting plane, caused by the eddy currents that are established by the moving coil above. (a) When the speed of the superconducting coils is low, the previous images move away from the plane (and the real coils) relatively slowly, allowing the eddy currents to produce a force on the coil in the direction opposite its motion. (b) When the speed of the superconducting coils is high, the images move away relatively quickly, allowing the lifting force to approach the ideal image force. (Reproduced from Rossing.)
As the train increases speed, the distance between successive images appears to increase, until the point at which the lifting force is best approximated by the repulsive force that would be produced if an exact image of the superconducting coils existed an equal distance beneath the tracks. This force is called the ideal image force, and is essentially the limiting value of the lifting force on the moving object.
In order to quantify the lifting force, I attempted to use the following equation, given in Jayawant:
(1) 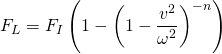
which relates the ratio of the lifting force ![]() and the ideal image force
and the ideal image force ![]() to the speed
to the speed ![]() of the moving coils (speed of the train) and the recession speed
of the moving coils (speed of the train) and the recession speed ![]() of the coil’s images inside the conducting plane, and
of the coil’s images inside the conducting plane, and ![]() is related to the dimensions of the coil. However, when graphing this function (the ratio of
is related to the dimensions of the coil. However, when graphing this function (the ratio of ![]() to
to ![]() in Mathematica, the output did not seem to model the behavior that I predicted; the function did not increase steadily with increasing speed, nor did it asymptotically approach a value of 1.0. Thus, I followed an assumption suggested by Kraftmakher, and replaced this equation for the lifting force on a rectangular coil with the simplified equation for the lifting force on a magnetic dipole, given by Reitz as:
in Mathematica, the output did not seem to model the behavior that I predicted; the function did not increase steadily with increasing speed, nor did it asymptotically approach a value of 1.0. Thus, I followed an assumption suggested by Kraftmakher, and replaced this equation for the lifting force on a rectangular coil with the simplified equation for the lifting force on a magnetic dipole, given by Reitz as:
(2) ![]()
where ![]() is the magnetic dipole moment of the train’s coils,
is the magnetic dipole moment of the train’s coils, ![]() is the height of the train’s coils above the conducting plate (track coils),
is the height of the train’s coils above the conducting plate (track coils), ![]() is the speed of the train, and
is the speed of the train, and ![]() is the recession speed of the coil’s images. It is clear that in the limiting case where
is the recession speed of the coil’s images. It is clear that in the limiting case where ![]() , the lifting force approaches the ideal image force for the dipole configuration, given as the constant out front in the right side of the equation. With this relationship, I will be able to approximate what the lifting and drag forces would be on a coil of superconducting wire inside the moving train.
, the lifting force approaches the ideal image force for the dipole configuration, given as the constant out front in the right side of the equation. With this relationship, I will be able to approximate what the lifting and drag forces would be on a coil of superconducting wire inside the moving train.



Nice development. It would be good to have a footnote that reveals the exact source of your equations. Interesting that v and omega are used to identify speeds. I am wondering why the engineers like to use omega rather than v with some subscript for the recession speed?!