Phase Modulation | Modeling and Experimental Tools with Prof. Magnes

Phase modulation is not a very difficult concept to grasp. In my blog proposal I presented this equation

(1) $\begin{equation*} \frac{1}{n^{2}}=\frac{1}{{n_{0}}^{2}}}+rE+RE^2 \end{equation*}$

This allows you to change the index of refraction with an applied electric field. The speed a wave travels inside a new medium is equal to the speed of light in a vacuum divided by the index of refraction of the material $v=\frac{c}{n}$ . Using this relationship and the equation above, we have an expression that relates the applied electric field strength to the speed of the wave in inside the crystal.

(2) $\begin{equation*} {v^{2}}=\frac{c^{2}}{{n_{0}}^{2}}}+rEc^2+RE^2{c^2} \end{equation*}$

Once the wave exits the EoM it will have a shift in phase. Being able to vary the speed of the laser inside the crystal very slightly will give you the ability to modulate the phase of the laser so that you can have it exit the EoM at what ever point in its oscillation you wish.

Here is an animation showing a light wave entering a crystal and slowing down having its phase shifted. I could not figure out how to draw lines on the graph but the crystal is from 0 to $2\pi$

1 thought on “Phase Modulation”

chnadell April 30, 2012 at 7:55 pm

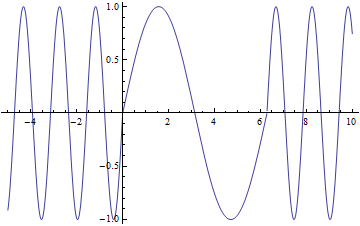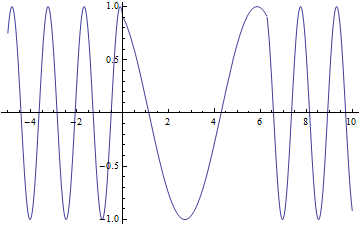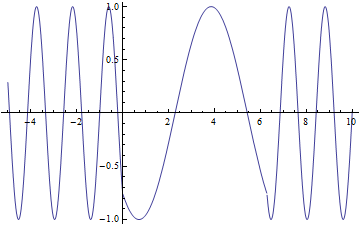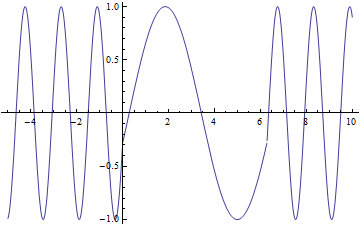
Your animation here is great for visualization! It could be even better if you found a way to make Mathematica slow it down though (this would have been a good trick for my project as well). Are the axes electric field vs. time?
Also, great explanation of the Jones vectors in the previous post- they really are a convenient way to write things out for EoM situations. Is there a neat way of notating the phase of the light as well?

Comments are closed.