4/27

I’ve been spending a lot of time with ParametricPlot, VectorPlot3D, and new things I hadn’t known about before like CoordinatesToCartesian, Evaluate, and Normalize (as suggested by Professor Magnes). Using these, I was able to correct several things. First I took my equation for the B-field and converted from spherical coordinates into Cartesian with the CoordinatesToCartesian utility, and was able to use this to plot with ParametricPlot. After this, I was able to break up the equation into each directional component, and plot in a 2D VectorPlot, as shown below.

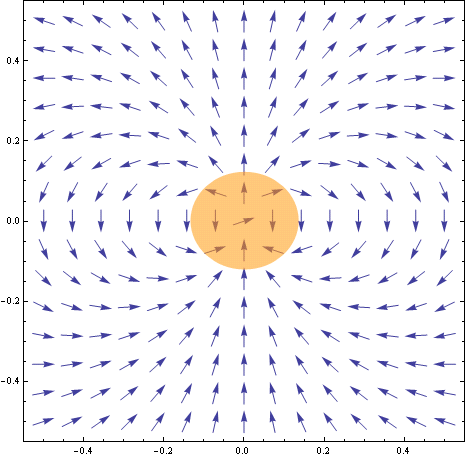
This is the kind of 2D graph of the vector field for magnetic force that I’d been attempting to get all along. The streamlines I’d been using previously were in lieu of vectors that simply weren’t showing up when plotted (although the streamlines did). The image above clearly shows the force of the magnetic field at all points around the sun (still assuming a stationary sun) in the xz plane.
After this, I was able to extend this process into a third dimension and get the following:

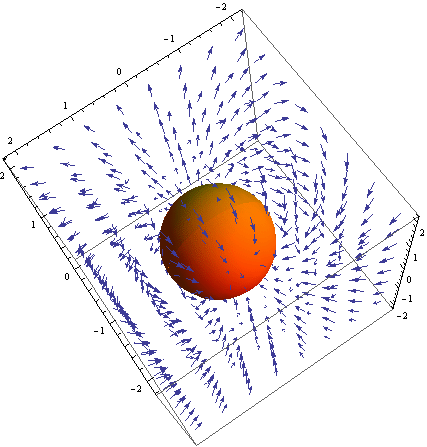
And from another viewing angle:

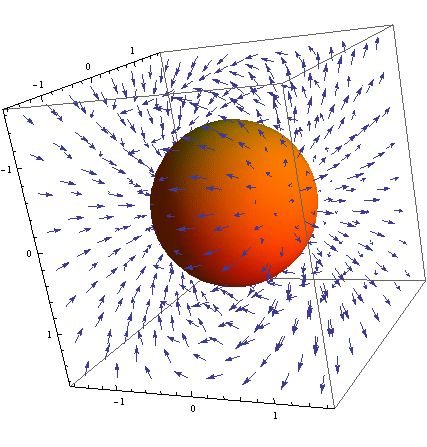
Looking at this final result, the vector field clearly goes from one pole (northern pole) and into the other (southern pole).
It wasn’t entirely clear to me how to approach the dependence of the magnetic field on latitude (and still isn’t really clear). I tried a sinusoidal dependence on phi, and converted this to Cartesian coordinates, and added it as a multiplicative factor to each component that it affected.

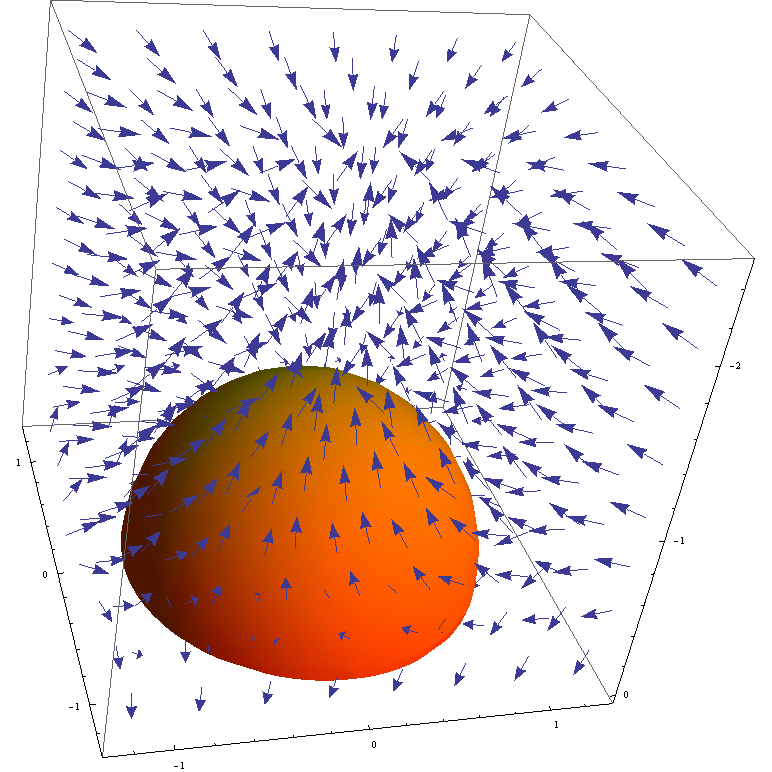
The above graphic shows a dependence on latitude, and the vectors near the equator are significantly smaller than those near the poles. So, after all of the trial and error, I finally have a result that shows a latitude dependence. However, even aside from the poor cropping, there are still directional issues introduced with an ArcCos function in the final equations which affects the final result; I think there are still some vectors that aren’t necessarily pointing the way they should be. The Mathematica notebook can be obtained here.
This result is similar to what we may expect for a very rudimentary picture of the sun’s magnetic field, in that the magnetic field at the equator should be less strong than that at the poles, similar to the Earth’s magnetic field. I think with more work on the force dependence on latitude, a more accurate picture could be obtained. However, even professional astronomers cannot fully predict and model the sun at any point in time due to its incredible complexity. Even with basic assumptions of a uniform rotation and uniform dependence on latitude, modeling the sun’s magnetic field is difficult; this difficulty is magnified with consideration of effects like differential rotation, tangling of magnetic field lines, sunspots, induced fields, etc.

——————————————————————————————

4/26

Update: A few things.
1. I tried to make the images larger– let me know if they’re still difficult to read. I know the first graph on my last post is a little blurry still, I’ll work on that.
2. A few mathematical mishaps were corrected, and I got a better response out of Mathematica for the magnetic field:

Here, the sun would be centered at the middle of the graph, at 0,0 (and note that it has a radius of 1 here, mostly for my convenience). The way I pictured this, it’s a z vs x plot, so that the z axis is the axis that the sun rotates around (pointing vertically up in the above image). This much more resembles the magnetic field of the sun that I was aiming for, although there still are directional issues that cause the arrows to go in opposite directions instead of one pole to the other.
I’m still having trouble with the ArcTan function in Mathematica. In between that and several square roots (due to the conversions between spherical and Cartesian coordinates), the signs of the streamlines get mixed up and Mathematica seems to be limited in this respect. I still have a few more things to try; I’ve been working with ParametricPlot all weekend and hope to get a more cohesive result soon by switching strategies.

——————————————————————————————

4/20

Proposal:
To recap, the goal of my project was to generally model the electric and magnetic fields of the sun, taking into account the effects of rotation. Our sun has several layers of plasma (hot, highly ionized material), which is a state of matter that does not adhere to the same properties as gases, liquids, or solids. Plasma on the sun generates a magnetic field through convection circulation. The sun has differential rotation, meaning that material at the equator actually rotates faster than the material at the poles of the sun. This differential rotation has a huge impact on the shape and strength of the sun’s magnetic field generated by the plasma.
The differential rotation and moving charges on the sun induce a complicated magnetic field. This magnetic field is furthermore responsible for much of solar activity: sunspots, solar flares, solar wind, all of which have a huge impact on our environment.

Assumptions:
There are several major assumptions that I undertook while starting to model the sun. The first was to consider the fields to be static, unchanging with time. Additionally, I worked starting with the electric field, and assuming that this induced the magnetic field; I did not deal with the electric field that the magnetic field would then induce in addition to the original.
When working with the latitude dependence for the magnetic field, I will first assume no dependence on latitude, then continue by assuming a linear dependence, and finally attempt to apply the actual rotational dependence to the magnetic field as determined in scientific papers.
Another major assumption that I worked under was that the dipole field is the dominant magnetic field for the sun. In reality, effects from differential rotation twist and break the magnetic field lines, and magnetized solar wind dominates at a further distance from the sun. Also as part of the effect of differential rotation, the sun’s magnetic field switches polarity every 11 years. The difference in polarity affects what is called the heliospheric current sheet (connected to the interplanetary magnetic field), which carries a small current. I ignored these effects in my model.

Model:
Below is the equation I examined to help model the effect of rotation on the sun:

With the values {a,b,c}={14.713,-2.396,-1.787} (Snodgrass 1990). The overall shape of this latitude effect is shown in the figure below. It is clear that rotation is not a linear trend and the rotation increases rapidly closer to the equator:

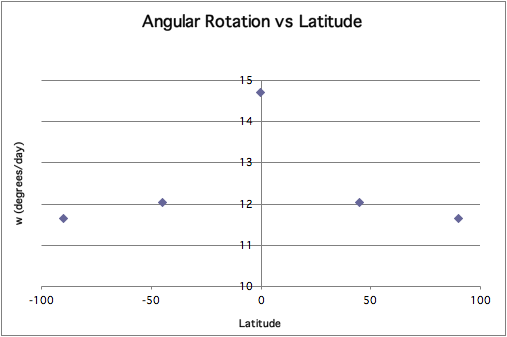
The charged particles on the surface of the sun follow the path of rotation at the surface; that is, they rotate counterclockwise, causing a counterclockwise electric field. The energy that the particles have is proportional to the speed of rotation at any particular latitude.

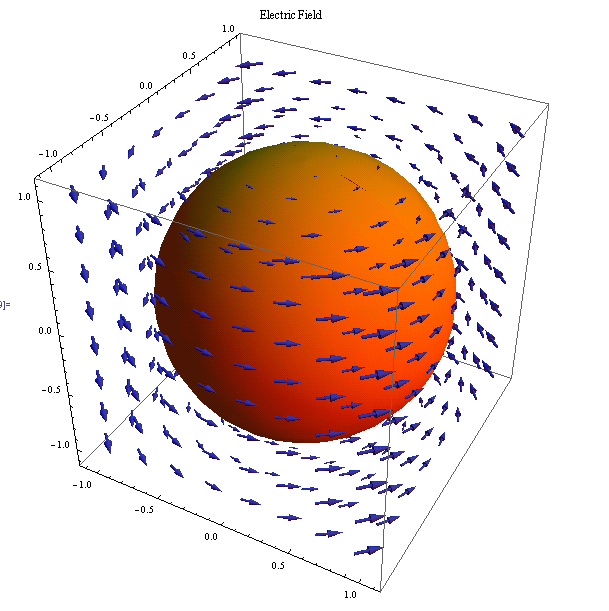
With the prior knowledge of the knowledge that the magnetic field follows a dipole form (prior to latitude dependency), we can use the Poynting vector to show us the direction of the electromagnetic radiation field, that of the intensity.

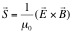
Such that if E curls around the sun, and we know that B will go from one pole to the other (south to north), S will then be the cross product of those two and point outwards.

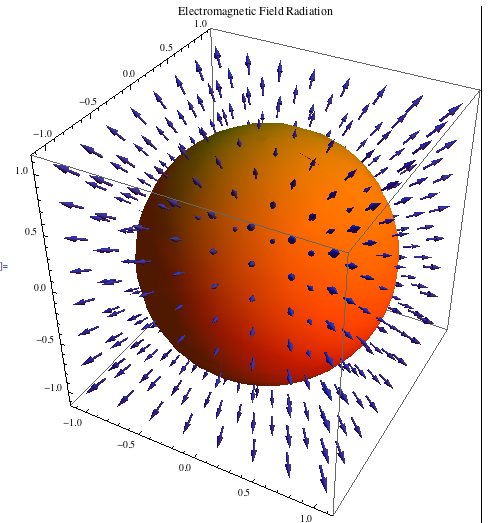
Conceptually, this makes perfect sense, as we know that the sun radiates outward in all directions.

To start modeling the magnetic field, I first assumed the field to follow the basic shape of a dipole in two dimensions:

Where k is the constant μ₀/4π (which for the purposes of modeling, was allowed to be k=1, since it ends up being only a scaling factor). I began with modeling the vector field two dimensionally in the xz plane. Adding in for the unit vectors:
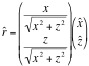and  

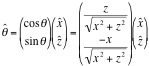
Substituting these into the previous equation,
B=

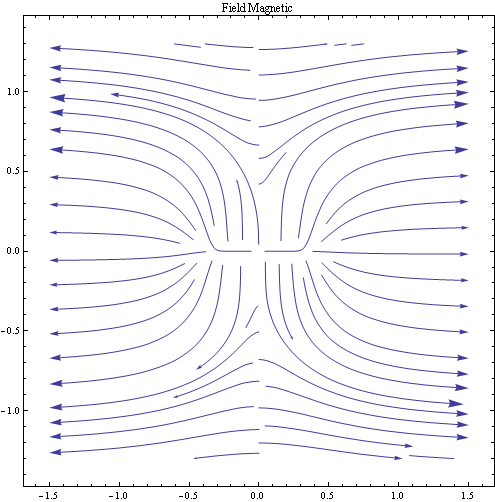
This gives the following 2D representation of the vector field.

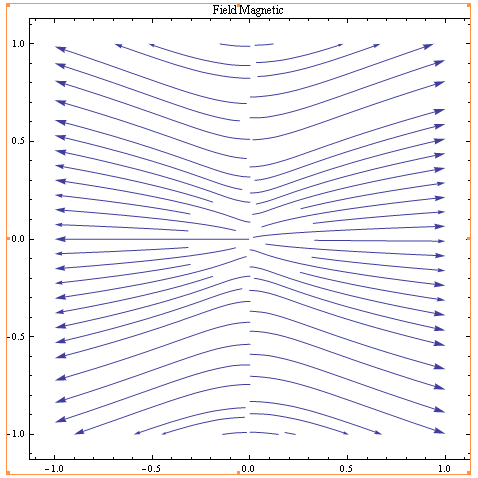
Note: Although this shows the general trend of the magnetic field for the sun, it is not completely accurate, and has an unresolved directional issue. The field lines should point from one direction to another only (rather that outwards from the center axis), and they loop around when a certain z limit (vetical axis) is reached. The Mathematica program approximates the ArcTan function between -π/2 and π/2, and this causes sign issues in the equation I’ve used (due to conversions between coordinate systems) leading to this result.

Another way to examine the magnetic field is to look at the partial derivatives in each direction to see the underlying changes in the plane. This new graph, still in the xz plane, is related to the magnetic potential of the sun and is more conceptually pleasing when thinking about the magnetic field of the sun. The messy mathematical details are here, if interested.

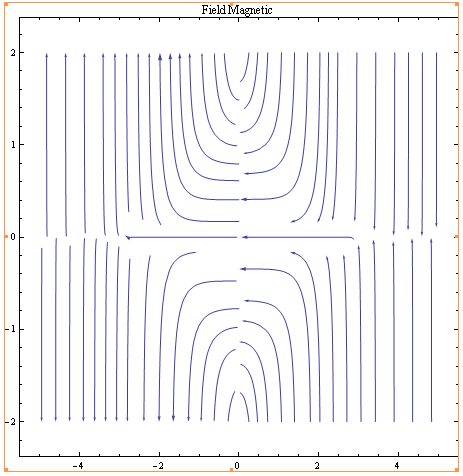
The above graph (the z is again on the vertical axis and x is on the horizontal) more tangibly shows the shape we expect the magnetic field lines to take. Assuming the dipole is oriented horizontally along the zero axis of the z-component, the lines continue straight along the dipole, but away from the dipole fan out and circle around at a distance from the dipole before returning to the axis, but still pointing in the same direction.

In the next week or so, I hope to further this model by putting the latitude dependence together with the magnetic field and moreover make the model for the magnetic field into three dimensions.

References:
Snodgrass, Herschel and Ulrich, Roger. “Rotation of Doppler Features in the Solar Photosphere”. The Astrophysical Journal 351 (1990): 309-316.

——————————————————————————————

4/19

TM Waveguide notebook – Electric Field, Magnetic Field

——————————————————————————————

3/29

Mathematica: Wave Animation

——————————————————————————————

3/21

I find that I write in my class journal rather sporadically. But, as the semester has progressed, my entries have become more focused on the material we’re covering in class, rather than random comments and thoughts, which in retrospect haven’t been particularly helpful. Most of my entries are very brief, mostly notes to myself to go over a concept I didn’t get the first time or to double check that I understand the use of a particular equation we used in class. Sometimes I rewrite concepts from Griffiths or from class in a way that makes more sense and is more along the lines of how I think about and comprehend physics.

I didn’t find my journal particularly useful for helping to pick out a project, as I haven’t really inserted those kinds of ideas into my journal (on the other hand this probably contributed to my not having any idea what to do for a project). I found my journal to be a little helpful as a starting point for studying for the first midterm, although mostly just as an outline for studying, not so much in actually studying. I would say the biggest help of the journal has been to help me grasp and internalize concepts that I needed to think about more deeply to really understand.

——————————————————————————————

Blog Proposal:

The plasma underneath the photospheric surface of the sun causes differential rotation, such that the material at the equator of the sun moves more quickly than that at the poles. This leads to the magnetic field lines of the sun being twisted and convoluted. The shape of the resulting magnetic field is most easily seen during a total solar eclipse, when the shape of the corona is visible.

Modeling the sun’s differential rotation and subsequent magnetic field, and especially the hot, highly ionized corona, is useful in helping to interpret the reason behind extreme coronal temperature, a problem in solar physics thus far unexplained. Additionally, the effect of the sun’s magnetic field permeates the entire solar system, often affecting our daily lives.

——————————————————————————————

2/11

Mathematica Notebook for Snell’s Law

In the second half of the notebook, I haven’t quite yet figured out how to conveniently make the different thetas appear distinct in the plot. I know you can simply rewrite the function for each theta to make them appear distinct (with dashed or colored lines or whatever), and plot them all on the same graph, but I feel like there should be an easier way. If anyone figures it out, let me know…

——————————————————————————————

2/7

Mathematica Notebook for Griffiths problem 4.10.

——————————————————————————————

2/3

Wolfram Demonstrations

I was wandering around the Wolfram site and came across several E&M demonstrations relevant to what we’ve been doing in class.
Spherical Shell in a B-Field
Electric Potential of a Metallic Cylinder Surrounded by a Dielectric in an External E-Field
The dielectric demonstration has variable relative permittivity, which I thought was interesting to play with to watch the effect of the field in and around the dielectric.
There are also a couple basic electric and magnetic dipole demonstrations, if anyone is interested.