EUROPA MODELING

As a reminder to everyone, my goal with this project was to create an accurate model of the magnetic fields of Jupiter’s moon, Europa. Mathematica was used as the primary modeling program to look at three different models for Europa’s structure. The data used for the model will primarily be taken from measurements made by the NASA satellite ‘Galileo’ and will include any more recent data that is available. Europa is the smallest of four Galilean moons orbiting Jupiter. The relevance of modeling Europa’s fields in particular is that Europa has the most convincing evidence for a liquid ocean capable of supporting life. Using information based on observed electromagnetic, heat flow, and tectonic data, scientists have been able to model several different possible structures for Europa’s interior, the most convincing of which is the subterranean ocean investigated here. The reasons for a liquid saltwater ocean is that the layer needs to be a conducter, and pure saltwater is a stronger conducter than freshwater. This is because the presence of salt provides ions, which in turn can interact with the plasma, and serve as the ‘free charge’ we rely on to induce fields.  The argument for a liquid ocean rather than a solid ice layer follows the same argument, as salt settles out of water during freezing. Thus, all solid ice is actually composed of freshwater, and despite its location atop a salt-water ocean, it would lack the ions allowing induction, thus the solid ice layer here is actually an insulator. Because the permeability of this layer is comparable to that of free-space, the effects of having a surrounding ice layer are neglected.  Also, the known average density of Europa places a bound on the depth of the ocean.  The value of ~3.02 g/cm^2 implies that the moon is composed primarily of silicates, which must be accounted for in the final model.

Methods

Serious assumptions had to be made for these models. First, and possibly most importantly, is that I had to treat Europa as being stationary in space. In reality, Europa has both rotational and transverse velocity, orbiting through Jupiter’s variable Magnetosphere. Were this magnetosphere more constant, the transverse motion could be more easily accounted for. The second important assumption made was for the free charge density of the saltwater ocean, which is highly dependent upon environmental factors. Both the volume charge density and surface charge density were estimated. The final major assumption was that the motion of the ocean is dominated by the rotation of the planet rather than by convection, this allows for the magnetic field to be most appropriately modeled by the dipole contribution.

Values assumed to be certain:

Europa Radius: 1569 km

Period of Rotation: 3.551 days (2.068 x 10^5 seconds)

The B-field is assumed to be created by the rotation of the conducting layer, since the water (and thus charges) rotate at different velocities as a function of both the radial distance (r), and the latitude (θ), we have a varying current.  Thus, the models examine three different structural possibilities for said conducting layer. With each model, the magnetic dipole moment was found for the given charge distribution, following which the magnetic potential (A) due to a dipole was solved for. Finally, the magnetic field could be found from the curl of the potential.

The equations used were:

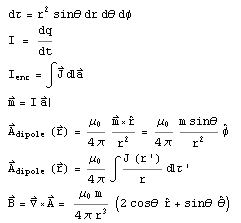
Models

The first model is just of a conducting shell.  The most analogous physical interpretation would be of a highly conducting puddle (infinitesimally thin) covering the surface of the planet.  Though this is not realistic, it serves valuable for the sake of comparison with the other models.

Solving the equations gives:

and,

The next model is of a solid, uniformly charged sphere.  While this is also not entirely realistic, it is a step in the direction towards an ocean, where the charge density relies upon the number of free ions (salt) in the ocean.  When solved, the magnetic dipole moment and B field become:

and,

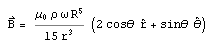
Finally, the third (and most physically realizable) model is that of a subterranean ocean.

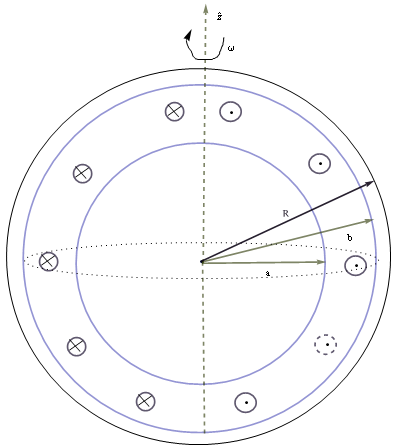
Where:

a = ocean’s inner radius

b = ocean’s outer radius

R = radius of Europa

ω = angular velocity

The dipole moment and B-field are:

and,

Results:

 

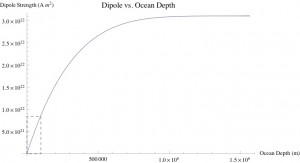
As one might expect, the dipole strength increases as a function of ocean depth.  Also, the magnetic field strength increases linearly with dipole strength.  Unfortunately, given the nature of all measurements made by the satelite Galileo, these modeled results are difficult to compare with.  However, given the physical problems in realizing the other two models, the subterranean ocean is the most likely model.  The images showing the surface of Europa, as well as heat-flow and tectonic data support this conclusion as opposed to a permanent fixed dipole.  Mostly due to surface features, scientists have calculated the surface layer of ice to be from 1-30 km thick.  Marked on the lower left corner of the graph above, the currently assumed depth of the ocean is ~100 km, giving a dipole strength of  [8.798×10^21] for a charge density of, ρ~10^(-15) [C/m^3].

_________________________________________________

~Wave Notebook~

enjoy!

~JOURNAL Summary~

As a second semester senior, I feel somewhat set in my ways when it comes to studying, and as such I haven’t used the journal TOO much in that sense.  However, there have been a few occasions where I jotted down notes that I found helpful when returning to study.  For example, Griffiths sometimes has an interesting or particular way of explaining a concept that stuck out to me and ended up in my journal.  When one of my classmates offers a particularly insightful  (or humorous) comment in class, I have included the quote in my journal.

I DO think that the journal will prove to be useful in my project to keep track of ideas and help guide my progress.  I’ve attached a copy of my proposal into my journal, and am allotting a specific space for ideas, roadblocks, and successes.  Hopefully the journal will be a solution to some of the organizational issues I have been known to have when working on projects.

—————————————————————————————————————————————-

PROJECT PROPOSAL

I hope to create an accurate model of the electric and magnetic fields of Jupiter’s moon, Europa.  I plan to use Mathematica as my primary modeling program, but will likely utilize Microsoft Excel as well.  The data used for the model will primarily be taken from measurements made by the NASA satellite ‘Galileo’ and will include any more recent data that is available.

Europa is the smallest of four Galilean moons orbiting Jupiter. Launched in 1989, ‘Galileo’ orbited Jupiter for 8 years before ending its mission in 2003.  In addition to Europa, Galileo also made many passes of Jupiter’s other moons Callisto, Io, and Ganymede.  The relevance of modeling Europa’s fields in particular is that Europa has the most convincing evidence for a liquid ocean capable of supporting life.

I will compare alternate models capable of producing magnetic fields with the currently accepted one for Europa and compare differences.  Factors investigated will include, but not be limited to: salinity, ocean depth, and rate of circulation/rotation.

—————————————————————————————————————————————-

Representations of the vector fields from problem 4.10 can be found here.

Also, one thing that I’ve found helpful when messing around in Mathematica is to have the notebook I’m working on only take up half the screen, and have the Mathematica “Documentation Center” filling the other.  This is found in the ‘Help’ drop-down menu…just search the term you want more information about (i.e. VectorPlot3D, etc.).  This allows for easy reference to the help menu which at least I use all the time.

Peace y’all