April 20, 2010:

The Electric Eel!

The Electrophorus Electricus, more commonly known as an electric eel, is one of the few creatures capable of generating, storing, and discharging electricity.  It uses this special ability for spatial awareness, similar to how bats use sound waves, and also to kill prey. Strangely enough, the electric eel is not an eel; it’s a fish! Living primarily in freshwater bodies of South America, electric eels can grow up to several feet long.

Generating Voltage

Inside the electrophorus are special cells called electrocytes. These cells are very similar to muscle fiber cells in that they can produce electric signals. Unlike muscle fiber cells, they cannot contract. These cells contain a high concentration of Potassium ions, a low concentration of sodium ions, and a comparable amount of negatively charged ions. The cell membrane is permeable to potassium ions but not sodium ions. When in this inactive state, the cell membrane has a negative voltage, preventing the potassium ions from flowing out of the cell.

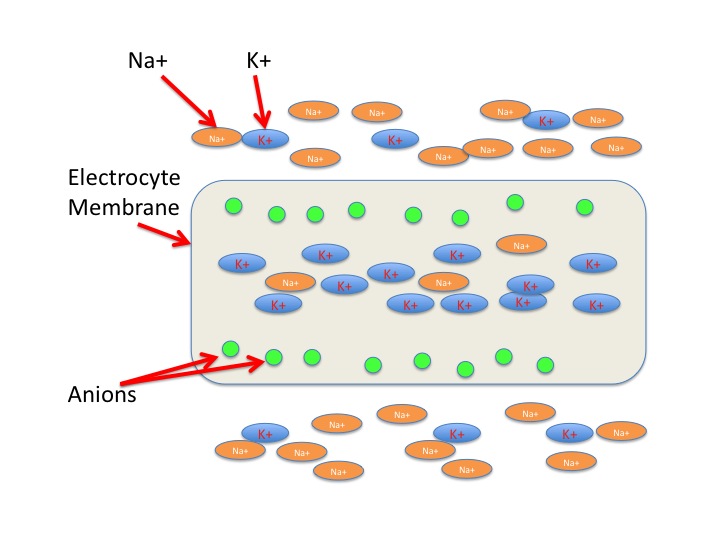
Acetylcholine, a neurotransmitter, can activate the electrocyte cells. It is secreted through nerves on one side of the cell, causing ion channels to open on that side. Sodium ions are able to rapidly enter the cell via these channels. This influx of positive charge alters the equilibrium potential of the cell. To Reestablish equilibrium, the potassium ions leave the cell on the other side, still very permeable to potassium.

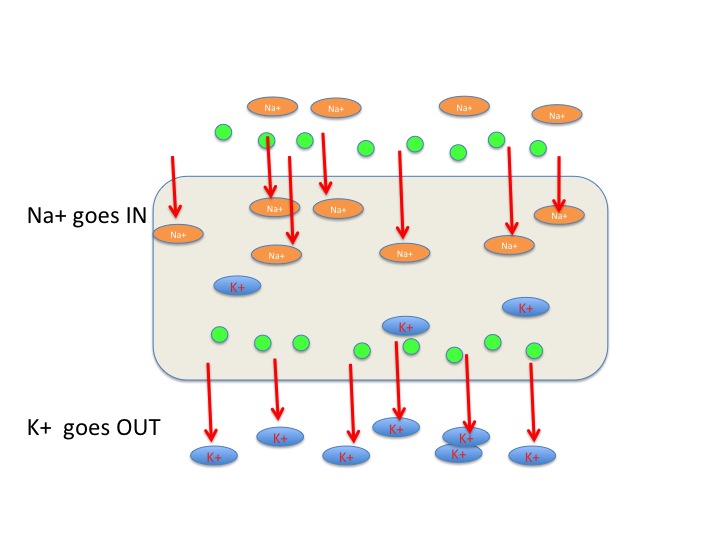
6000 of these electrocytes occupy about 4/5^th of the length of the eel, and when these cells are activated, the eel produces a current of 500V with the head of the eel having a positive charge and the tail having a negative charge. Differences in nerve path length enables the synchronized activation of thousands of these cells. Since electrocytes in the electric organ have a different distances to the brain (some may be inches away, others may be several feet away), the nerves of electrocytes in close proximity to the brain will have slower impulses and longer pathways.

In addition to putting out this high voltage shock, the electrophorus can also put out a low voltage pulse. This lower voltage can be used to “see” surrounding objects. Objects with a different conductivity will distort the electric field that the eel produces, thus making the eel aware of the object’s presence.

Let’s get down to Modeling!

I would like to model the electric field produced by the eel as a function of time. There’s a serious lack of information on how the eel physically generates this field. The fact that the eel produces a linear current does not explain how the eel generates an electric field surrounding it. I am going to make some massive assumptions and do my best to come up with a physical explanation for the field.

When the eel activates the electrocytes, current flows from the tail to the head. This would seem to imply that head of the eel has a positive charge and the tail has a negative charge when the cells are activated.  I’m going to treat the head and tail as a dipole system, with the head having a positive charge and the tail a negative charge.

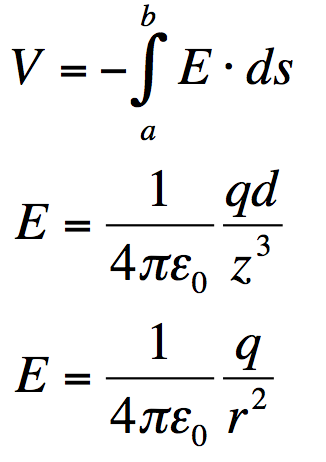I can find the magnitude of the electric field between these two poles if I assume the eel is about 2m long and that the potential drop is 600V. This is not the electric field I ultimately want to find. This electric field will allow me to find the amount of charge at the head and tail, which will allow me to model the dipole. I can find the charge by treating the electric field halfway between the two poles as being due to two point charges (at the poles). I use the equations as seen on the left. I calculated that the dipole charges have a magnitude of 33nC.

Below is a model of the electric field created by the Eel during cell activation. The poles are separated by 2 m and have a charge of 33nC and -33nC. First, here are the equations I used to construct this graph: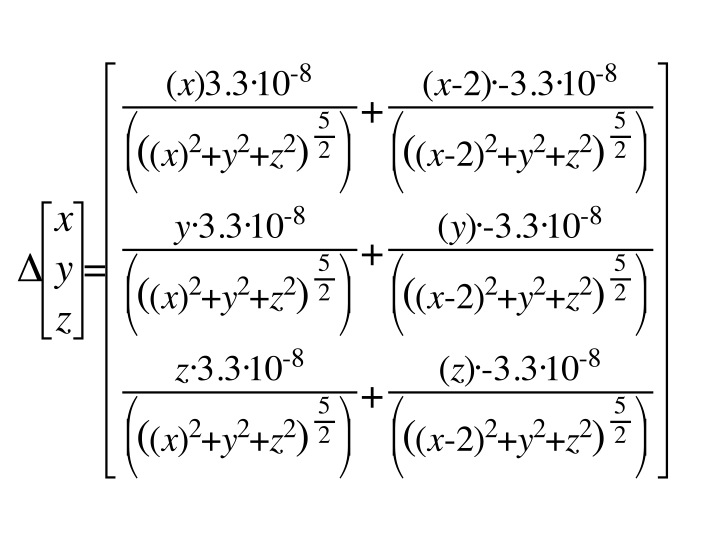

The Electric eel discharges the current in 2 ms, that’s 2 thousandths of a second! Here’s how the electric field changes in magnitude over the course of those 2ms:

Check out this cool 10 min film from the 1950s! Watch five people holding hands (in series) feel the shock!

References:

“Ask the Experts.” Scientific American Mar. 2006. Print.

Bauer, R. “Electric Organ Discharge (EOD) and Prey Capture Behaviour in the Electric Eel, Electrophorus Electricus.” Behavioral Ecology and Sociobiology 4.4 (1979): 311-19. JSTOR. Web. 25 Mar. 2010. <http://www.jstor.org/stable/4599204>.

“Electric Organ (Biology).” Access Science. McGraw-Hill. Web. 25 Mar. 2010. <http://www.accessscience.com>.

Keynes, Richard D. “The Discharge Mechanism of Electric Organs.” Trends in Neurosciences 25.1 (2002): 55-56. Web. <http://tins.trends.com>.

April 20, 2010:

Here’s my Rectangular Waveguide for TM

March 28, 2010: Here’s some sweet waves.

March 22, 2010: Excerpts from, The Journal

Although I did not write in my journal every day, I made use of it. While learning material, I kept track of concepts that I struggled with. This was useful when study time came around. I also keep track of zany EM ideas I think of. It’s cool flipping back through the pages and seeing all the crazy ideas I came up with. Good memories. I also was able to use my journal as a calendar of sorts to keep up with all the EM assignments. I did not find my journal particularly useful in digesting material. Overall, I like the idea of the journal, but I think it’s a tad superfluous. From a few years of experience as a student, I’ve honed some great study methods that work well for me. After experimenting with the journal and not finding any particular benefit over my normal methods of learning/studying/thinking, I think I’ll go back to my regular methods. That’s not to say that the journal doesn’t work well, however. I just prefer my own way.

March 3, 2010:

Electric Fields and Fish?

For my project I’d like to learn about how certain types of sea creatures create and use electric fields.  I will research the mechanisms by which electric eels are able to produce electric fields and then compare this to batteries.  I could draw diagrams to show the parallels between the eel and batteries. I may be able to produce some sort of model of the electric field generated by the eel as a function of time. Depending on how much work this is, I could also possibly study other fish use electric fields to determine their spatial position (like bats with sound waves).  I may be able to make a video using power point to show how these fish create electric fields.

Feb 15, 2010:

Here’s my mathematica fun with the dielectric version of snell’s law. No matter how hard I try, I cannot get total internal reflection! I conclude that dielectrics do not exactly follow snell’s law ( total internal reflection is not possible!).

Feb 8, 2010:

Here’s my mathematica thingy. I left out the constants since they don’t really affect the look of the graph.

I came upon a very enlightening youtube video the other day. It’s about space and time. There are actually FOUR simultaneous days in every rotation of the Earth..pretty sweet. check it out. . To find out more, check out www.timecube.com

Problem 4.1 issues

I’ve spent so much time trying to solve this problem!

The first method I used: W: integral(FdL). I use Coulomb’s Law for the force.

After thinking about more, I don’t think that Coulomb’s law is the right force to use. This is the force between charged particles. It will NOT cuase the electron to ionize, since this force will keep the electron in its orbit about the nucleus. Gabe used the equation F=Eq, which seems much more appropriate, since the hydrogen atom is placed in a capacitor (where there’s an electric field..).

I run into trouble when trying to set the limits of integration for the equation W=integral (Fdl): should it go from 0 to r, where r is the distance at which the electron has been ionized. Or do I integrate from R to r, where R is the initial distance between the electron and the nucleus? I haven’t been able to persuade myself yet on which integral to use, but I decided to use the former since it’s easier. I get an answer only one order of magnitude off from my answer calculated using Coulomb’s law.