Auther: Samuel Gilbert
Introduction:
This project models the propagation of a quantum wave packet in an infinite square well, and introduces between zero and three potential energy barriers. The wave packet used is a “Gaussian” wave packet (Eq. 1), and is a solution to the Schrödinger equation.
ψ(x,t=0) = C*exp[-(x-x0)2/σ2], (Eq. 1)
C is a constant that represents the magnitude of the wave packet, x is the position variable, x0 is the initial position of the wave packet, and σ is the initial width of the wave packet.
The program is designed to be highly interactive, and therefore requests three inputs from the user – the number of potential barriers, the strength of the potential barriers, and the initial energy of the wave packet. An initial setup with three potential barriers is shown below in Fig. 1:
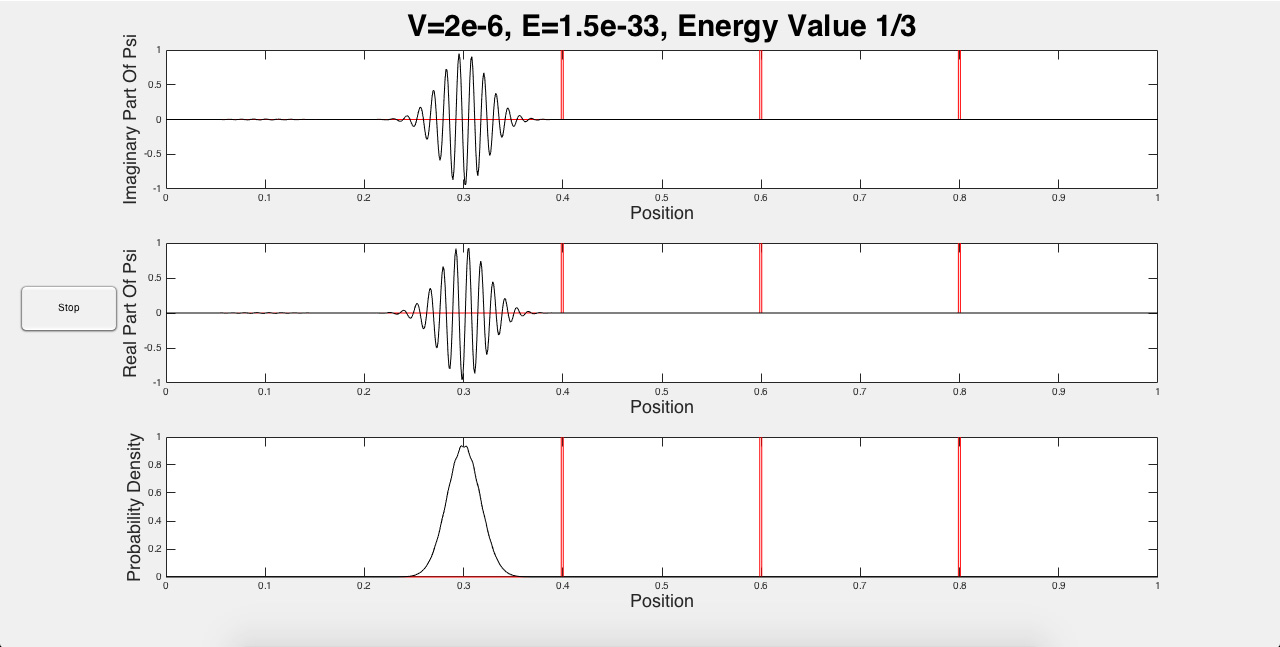
Fig. 1: Image of a sample initial setup.
The motivation for this program was to create an interactive education tool. To this end, the program provides instant feedback to changing variables such as energy of the wave packet and the strength of the barrier, which is a particularly useful tool in understanding quantum reflection, transmission, tunneling, and furthermore, the probabilistic nature of the quantum world.
Three plots are produced simultaneously – the imaginary part of the wave function, the real part of the wave function, and the probability density. In plotting the probability density, the program gives a visual representation of the fact that the position of a quantum object is not well defined, as it is governed by probability. The user will see the probability density split over a potential barrier, representing the probabilities of the wave packet being reflected or transmitted, respectively.
Methodology:
The computational method used in this program is the “leap-frog” method, as described in Giordano (1). The leap-frog method was used, because it allows for time dependence, unlike the shooting method studied in class. Our wave packet is then allowed to develop over time from the initial wave packet in Eq. 1., which it does. The leap-frog method alternates between evaluating the real and imaginary parts of the wave function. This, in essence, evaluates the wave function in ∆t/2 increments. In addition, it is notable that the time dependence of the Schrödinger equation is contained in the computational method itself, which is a beautiful way of handling time dependence. The leap-frog method can be thought of as an adapted Euler-Cromer method, as the updated real part of the wave function is then used to calculate the updated imaginary part, and so on throughout the routine. Giordano (1) cites that the leap-frog method has a numerical error of the same order as the 2nd order Runge-Kutta method. A significant portion of the code was dedicated to interactivity, and therefore deals with the presentation of the animated plots. This includes the stop button on the plots, which calls an external function which closes all windows, and also making sure the animation runs for the right amount of time.
Results:
Fig. 2 below shows three animated gifs for three different energies with one potential barrier.
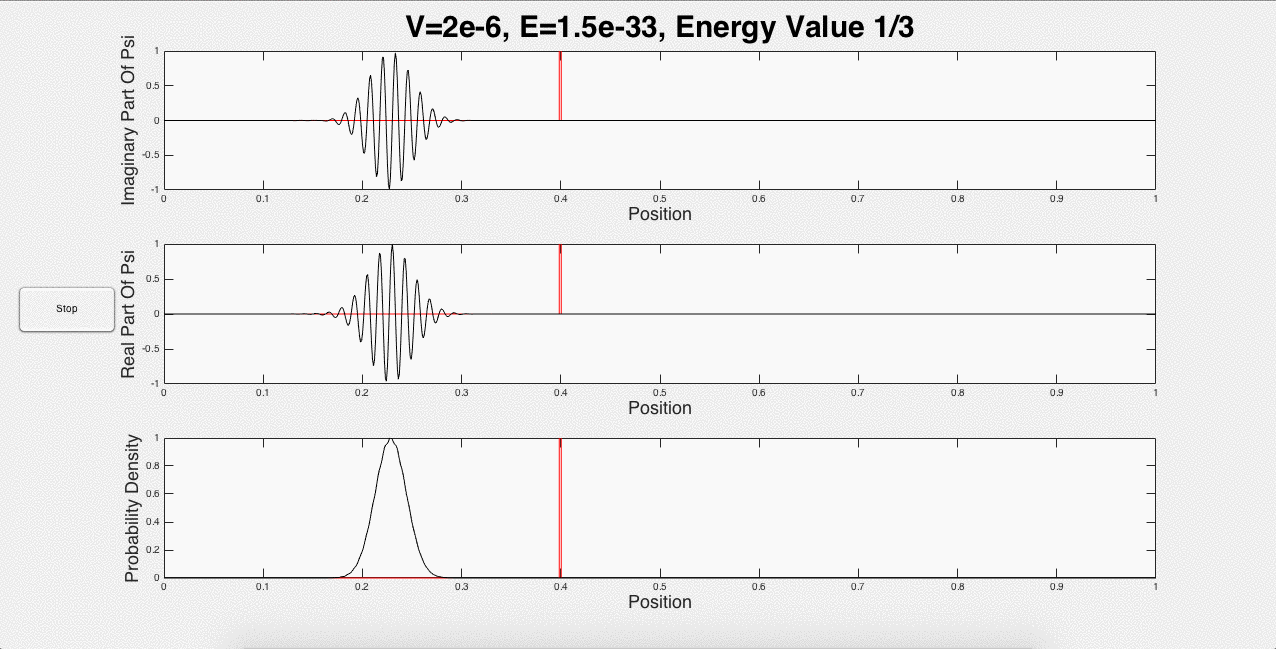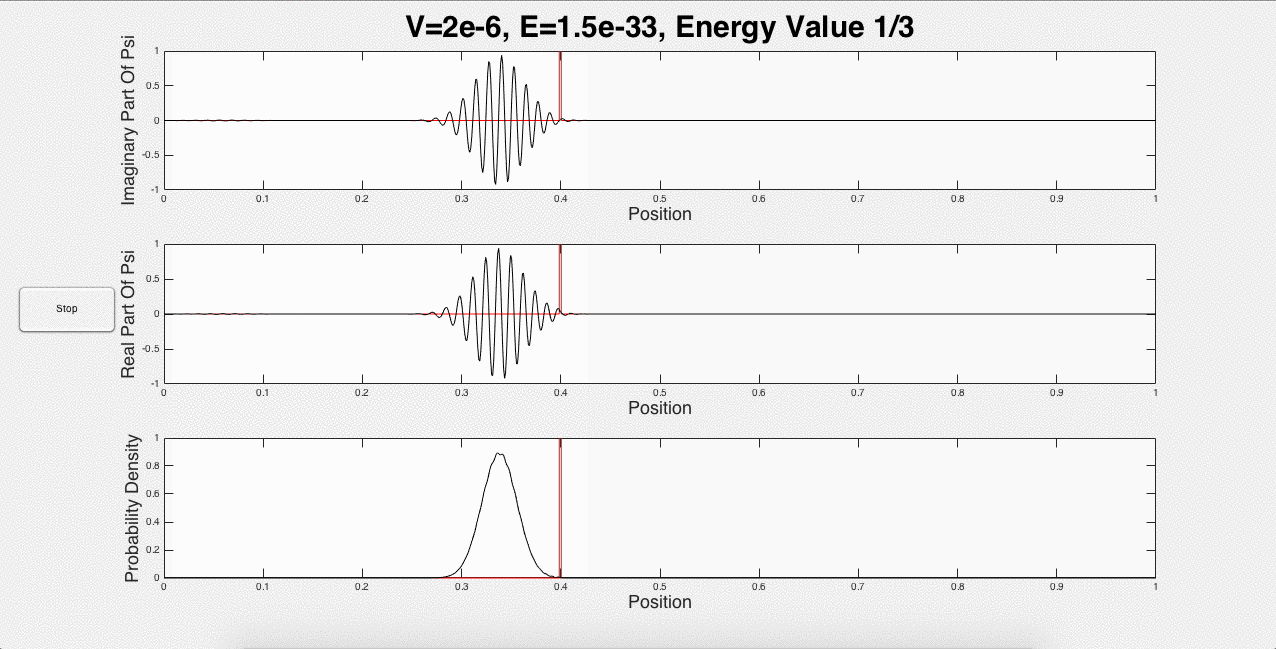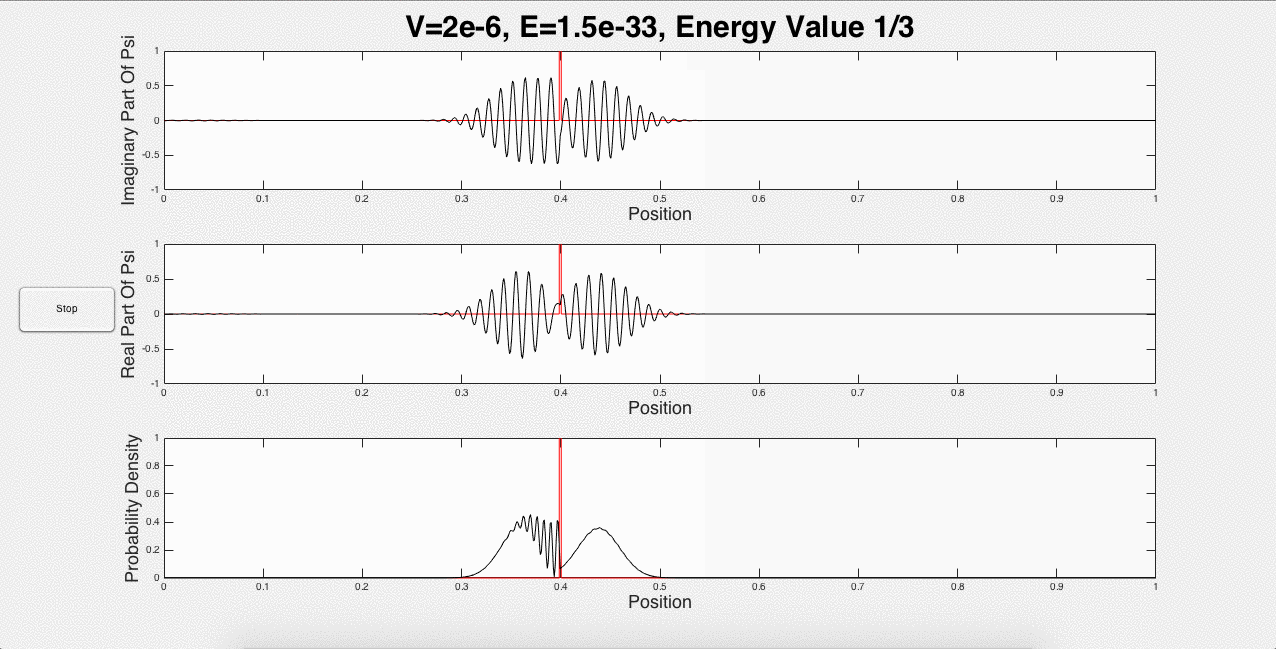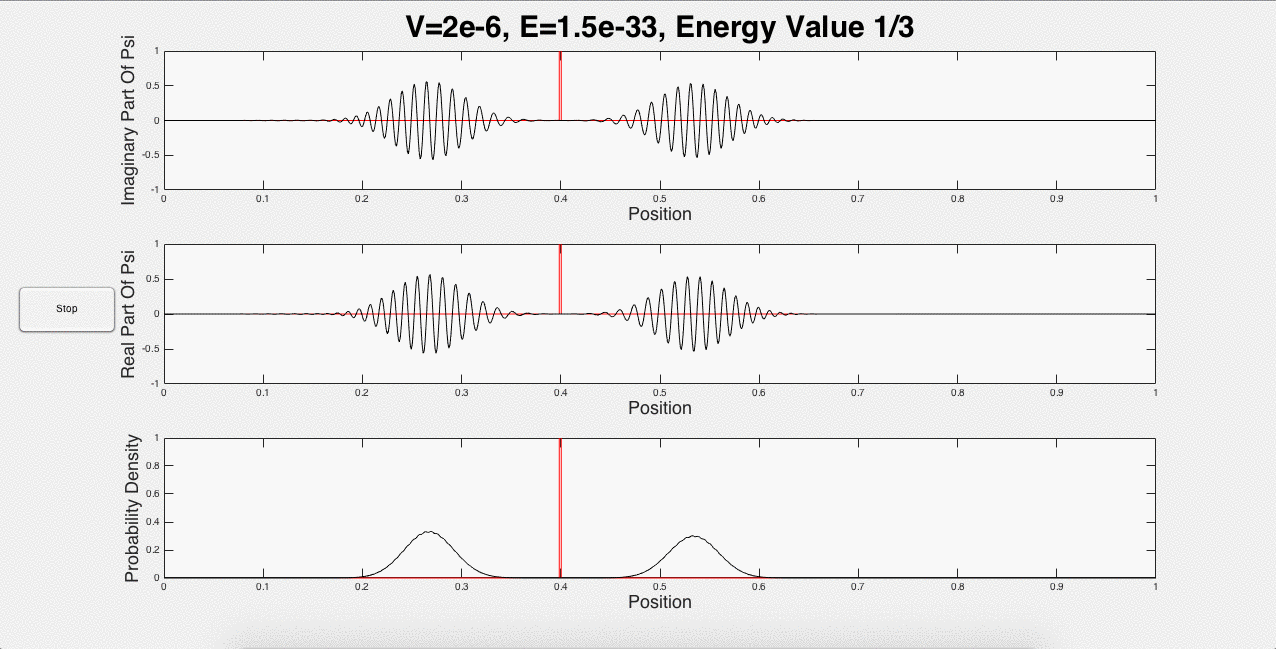
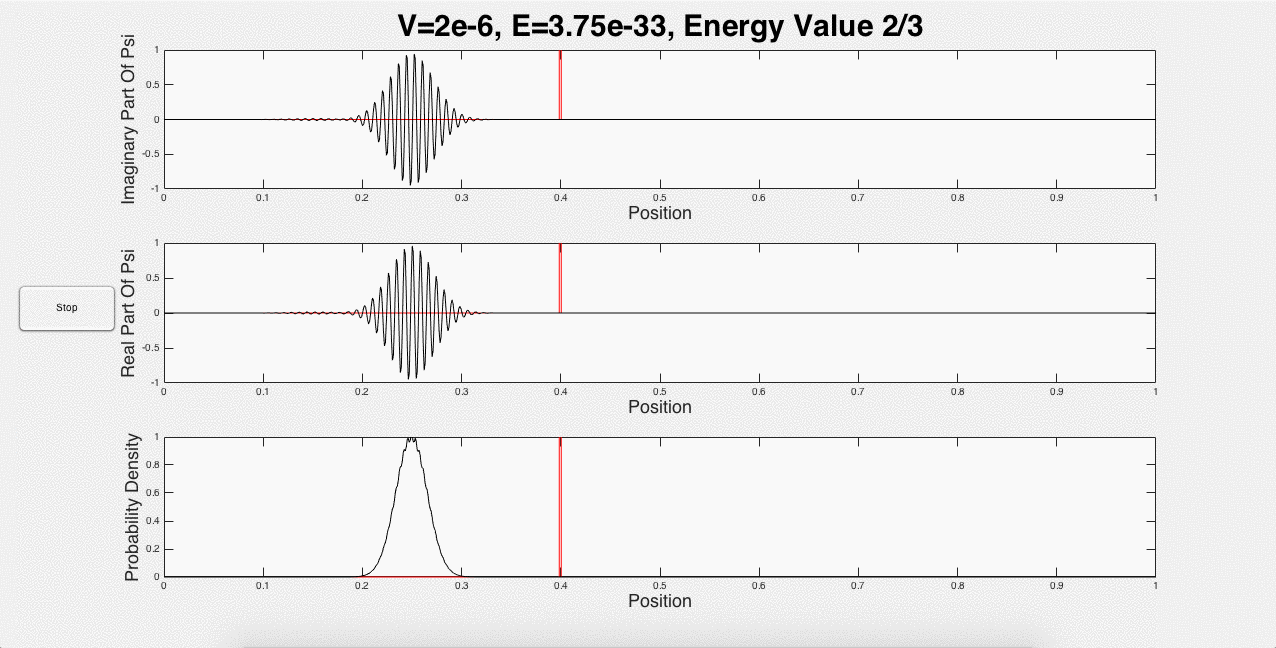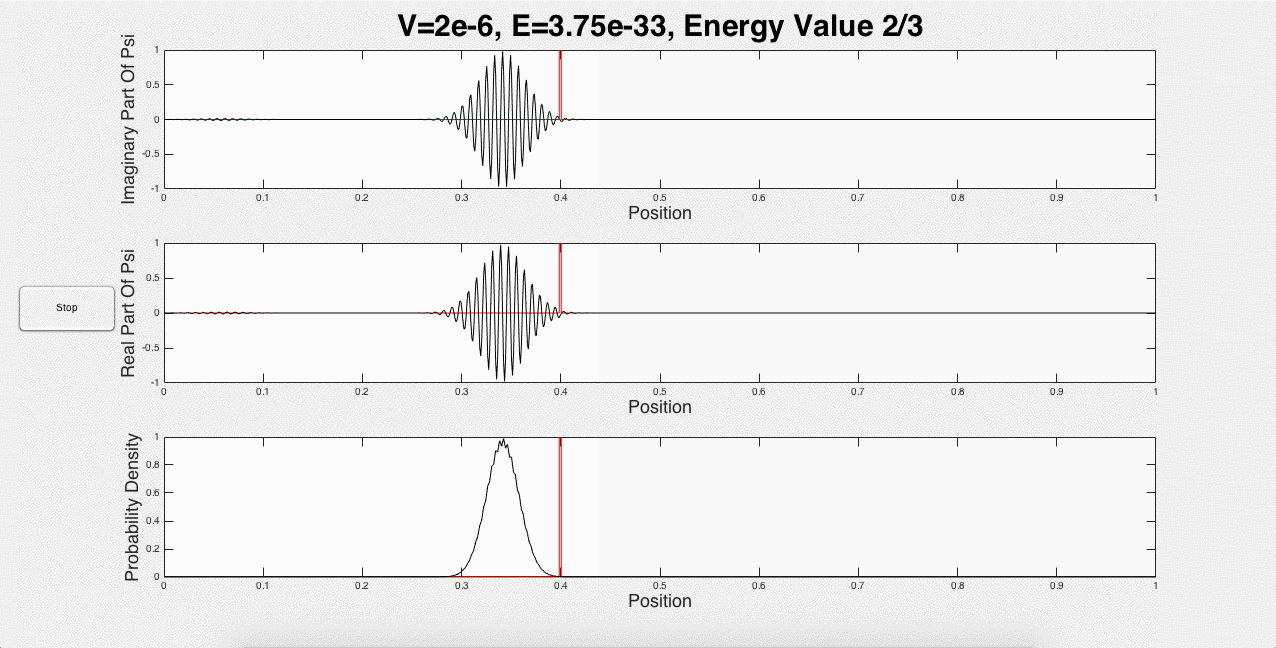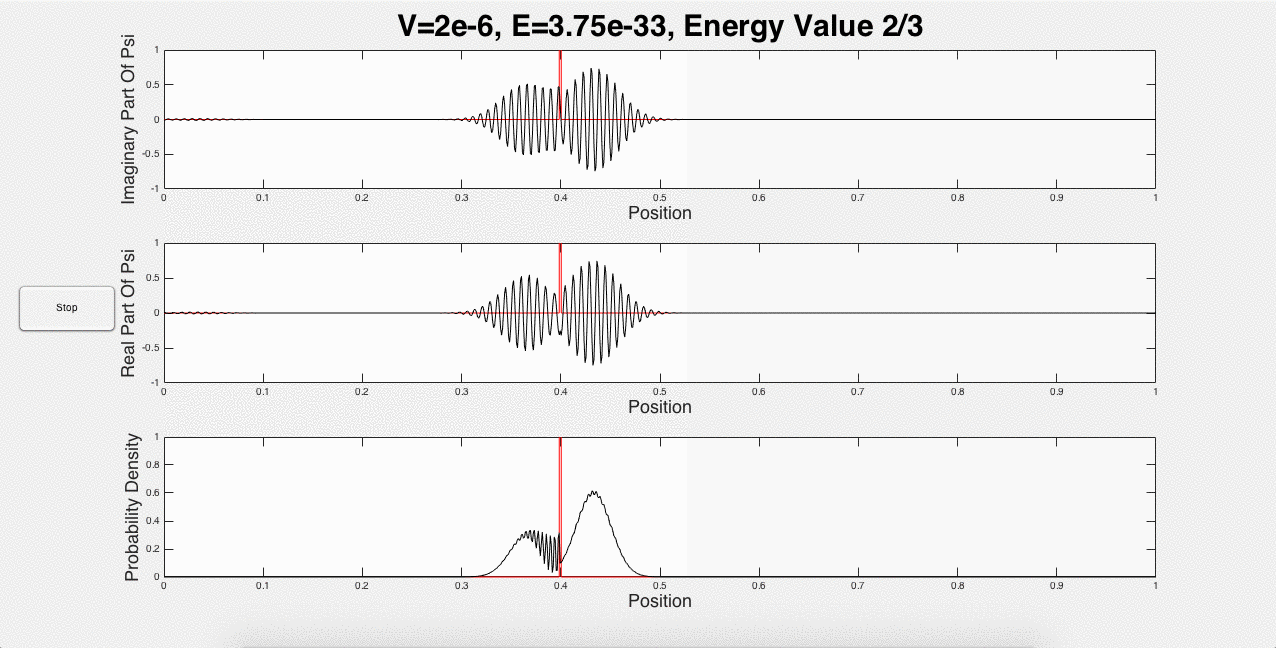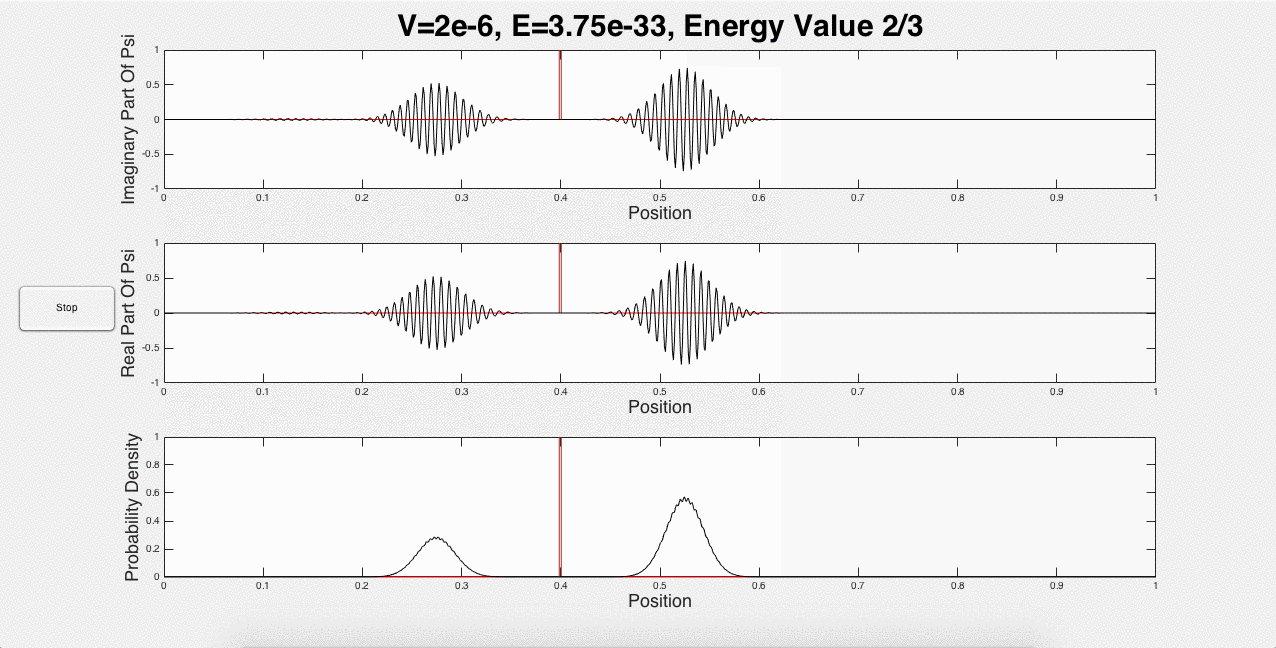
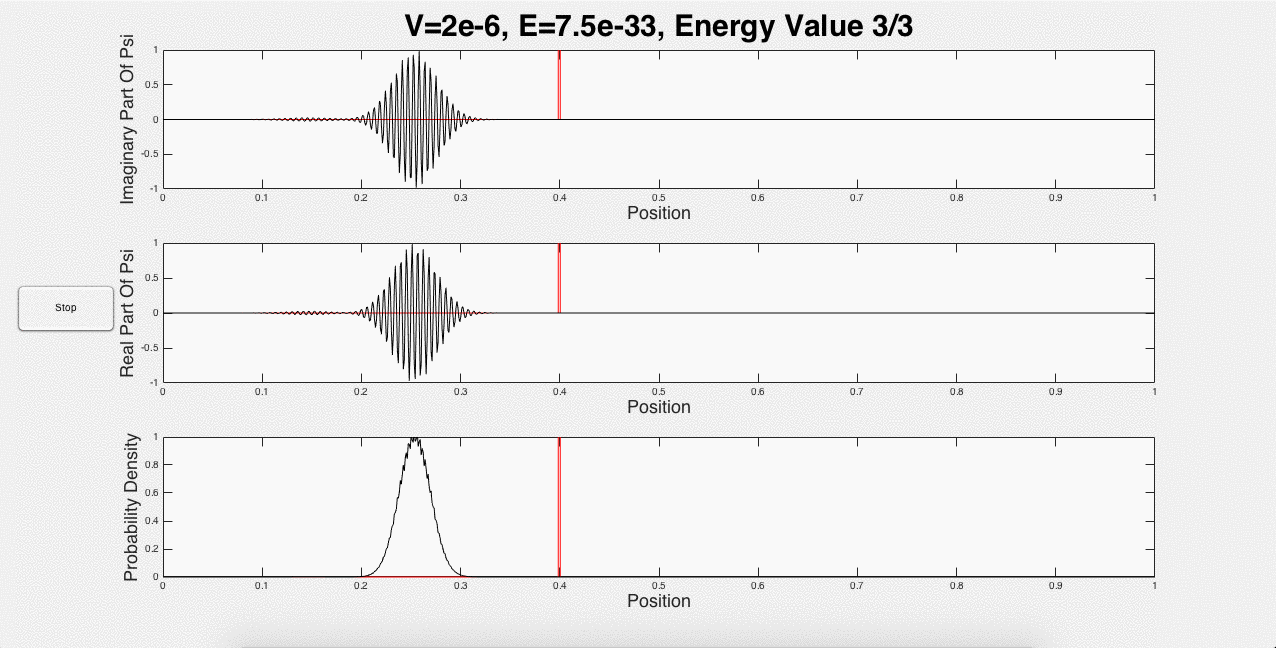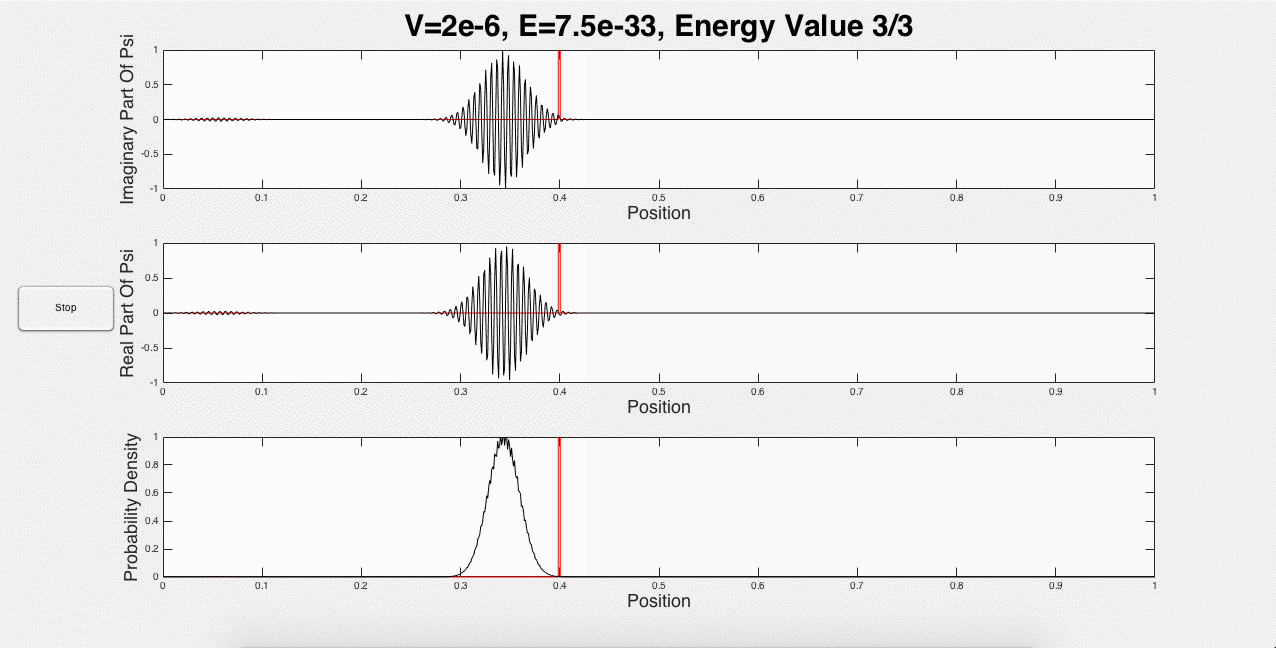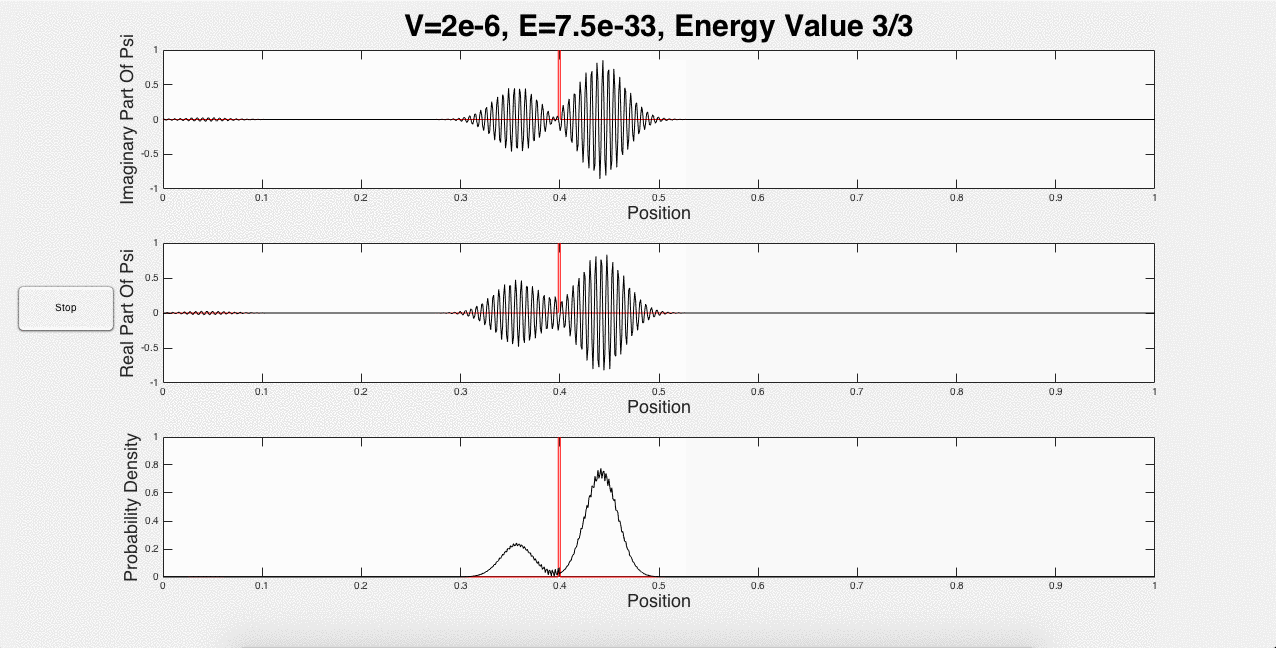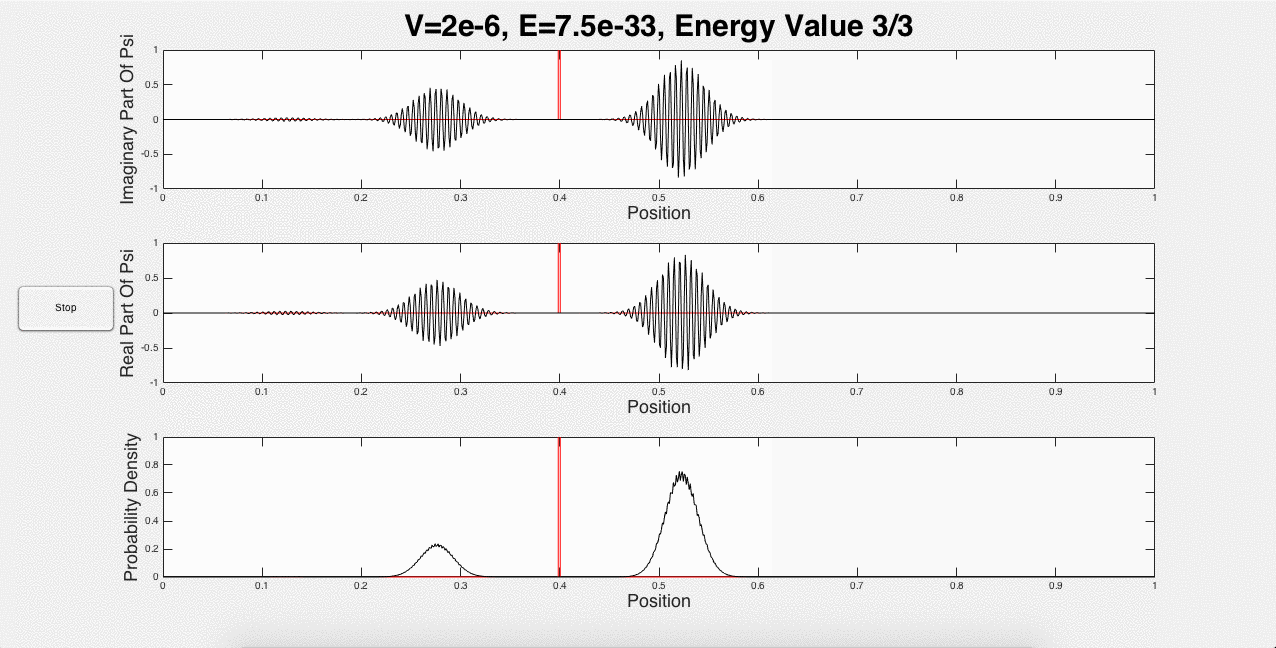
Fig. 2: One potential barrier modeled for three different energies.
These three animations represent what a user would see if the inputs were 1 potential barrier of strength 2*10-6, and a wave packet with initial energy of 1.5*10-33. This is just one of the many options that a user can choose. For example, the user can explore using the same initial energy, but changing the strength of the barrier. In addition, portions of the wave packet can get caught between two potential barriers, and add constructively, as shown below in Fig. 3:
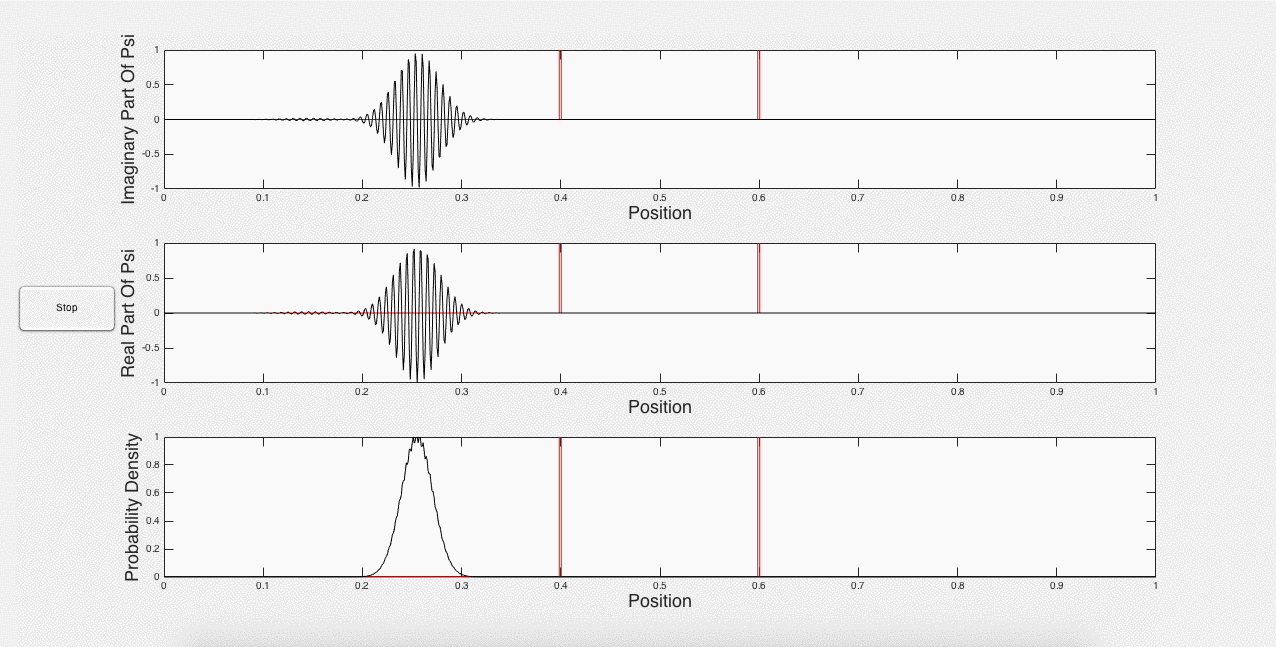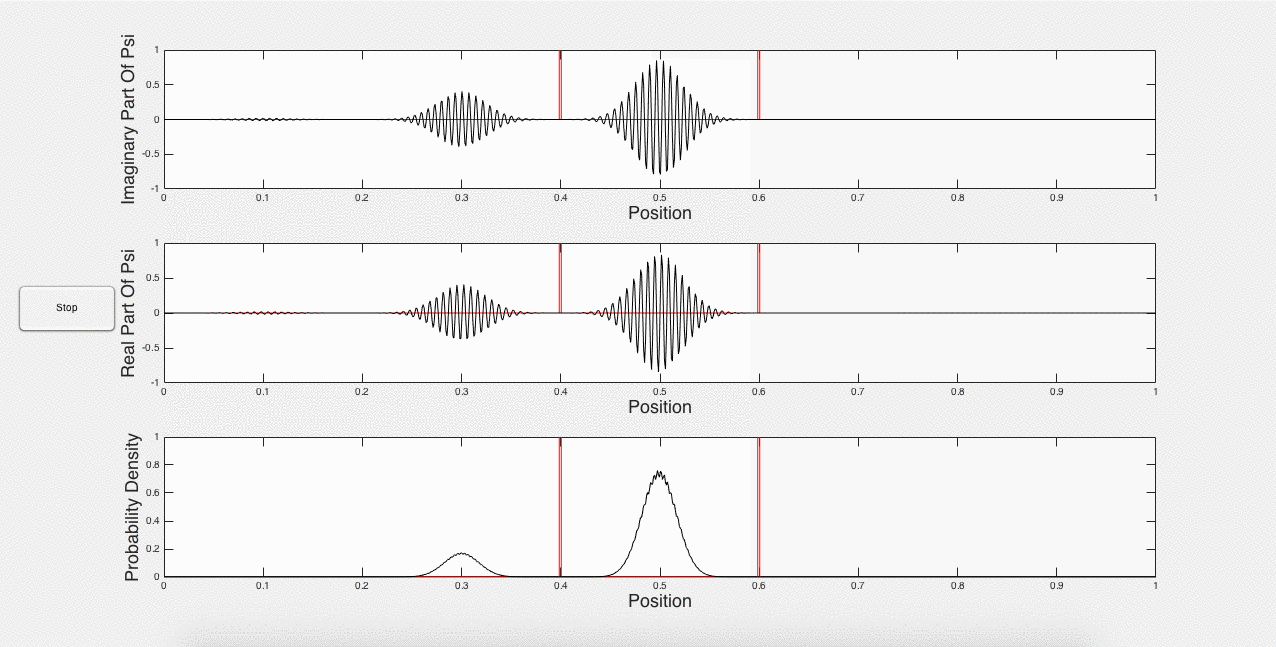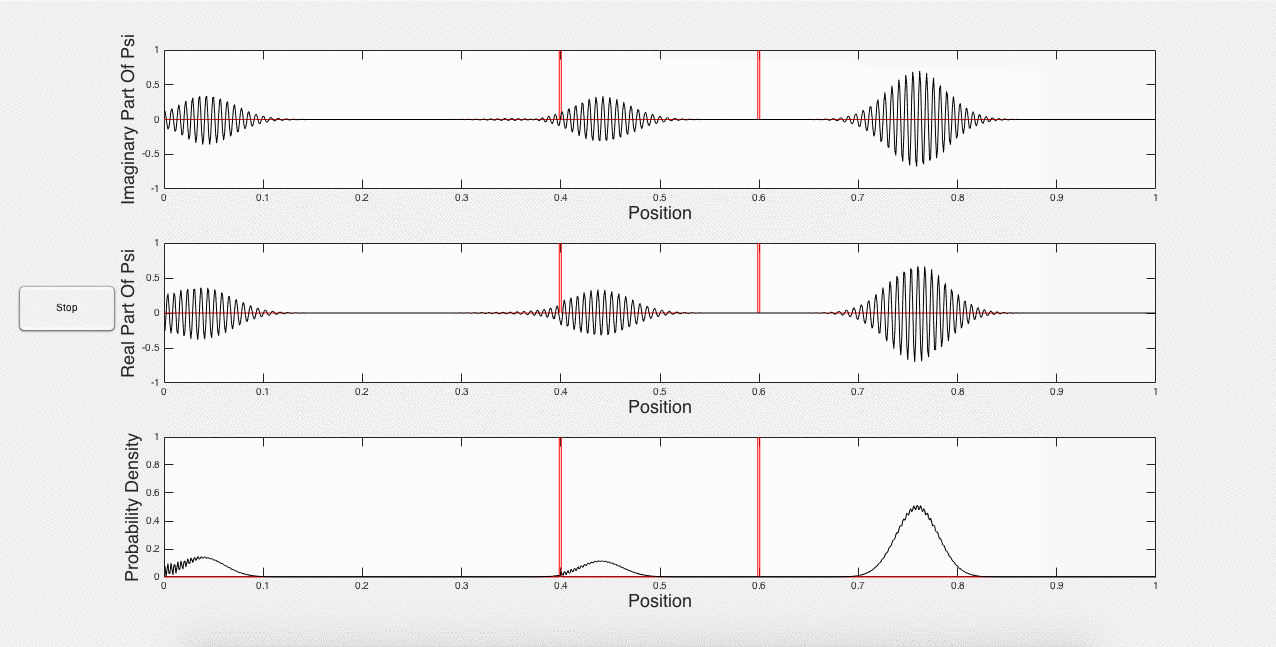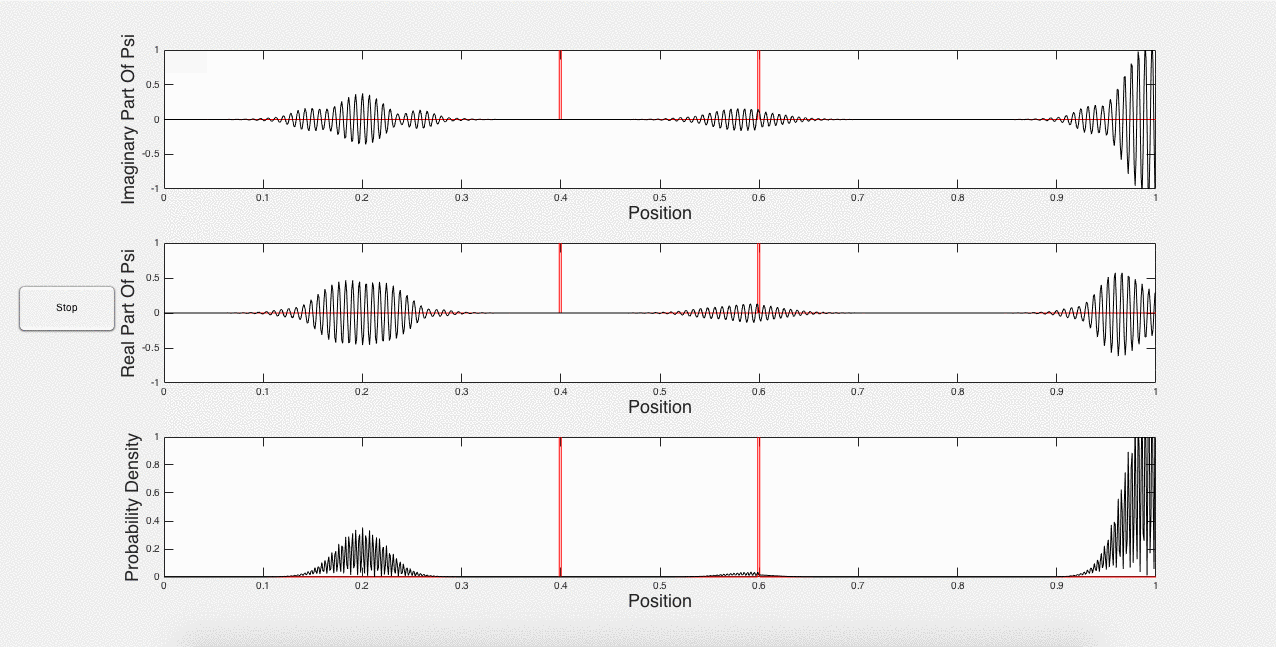
Fig. 3: Wave packet caught between barriers, and constructive interference.
The wave functions can get complicated very fast by adding enough potential barriers and letting the program run long enough. These simulations therefore allow for complex systems than could be modeled by hand.
Analysis:
One of the unexpected results of this program is that the Gaussian wave packet decays over time, as shown below in Fig. 4.
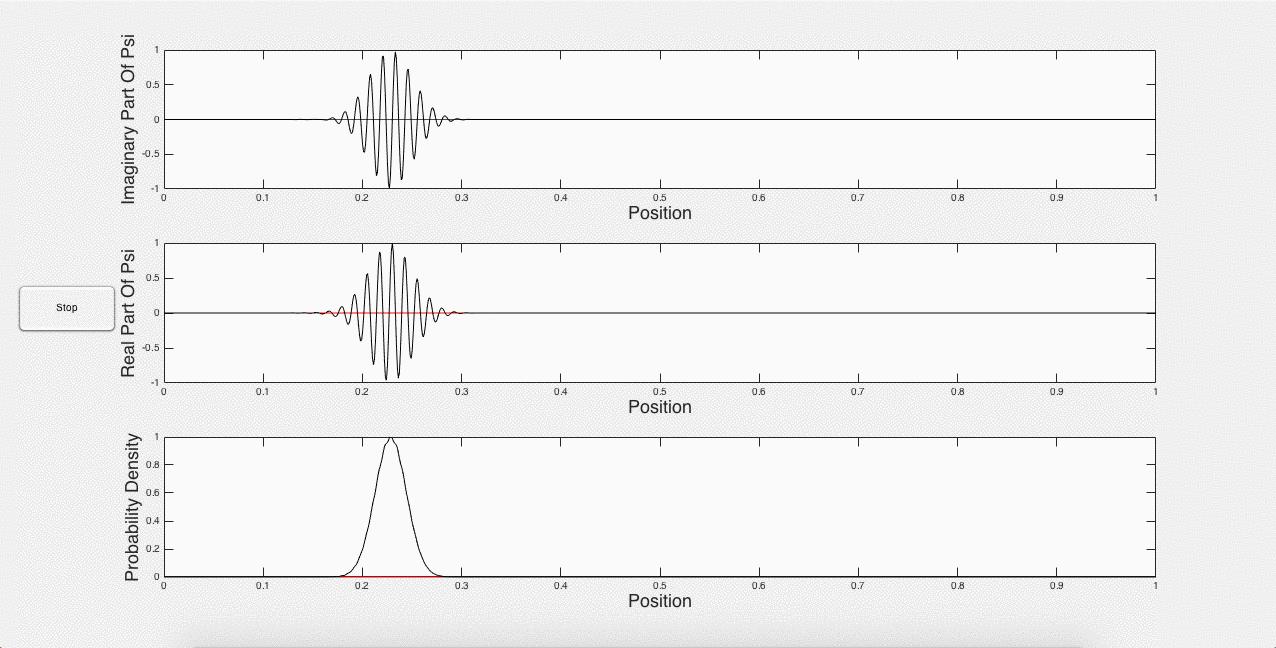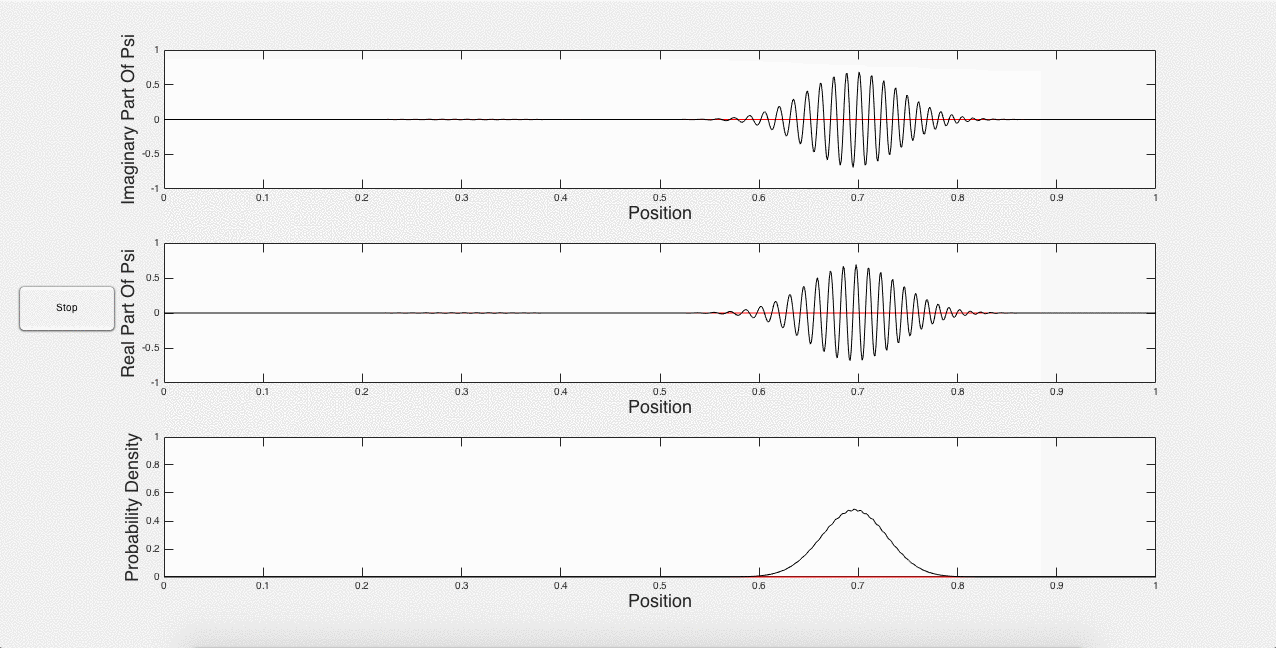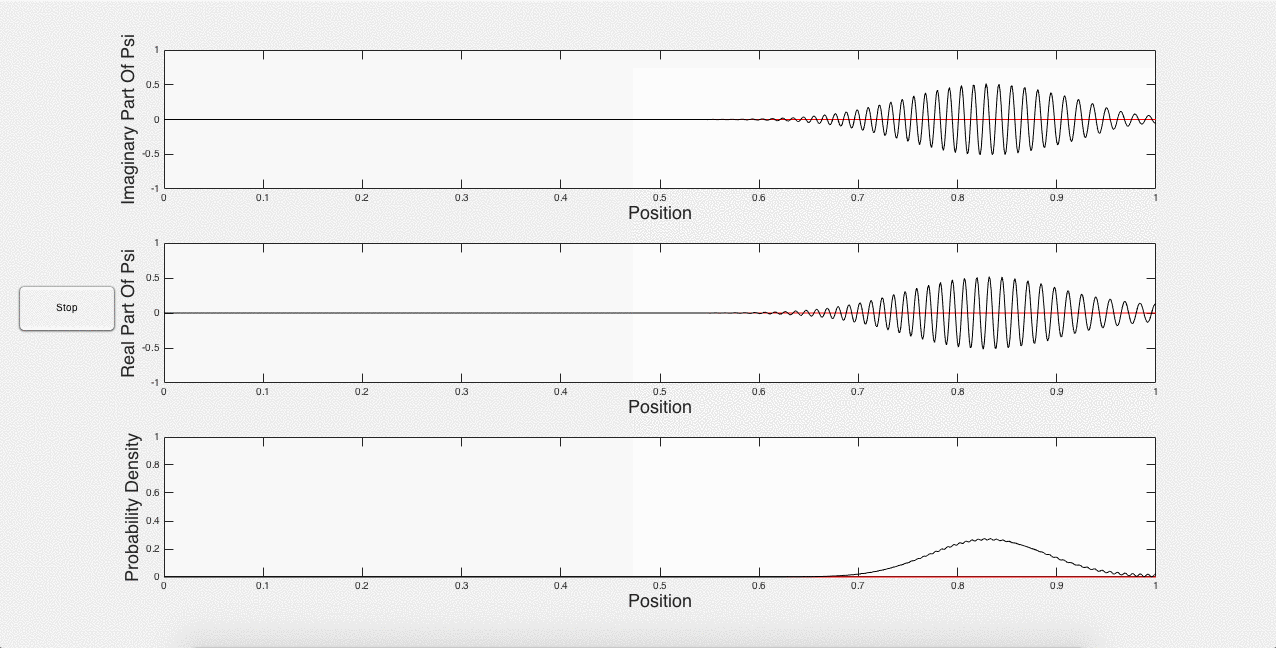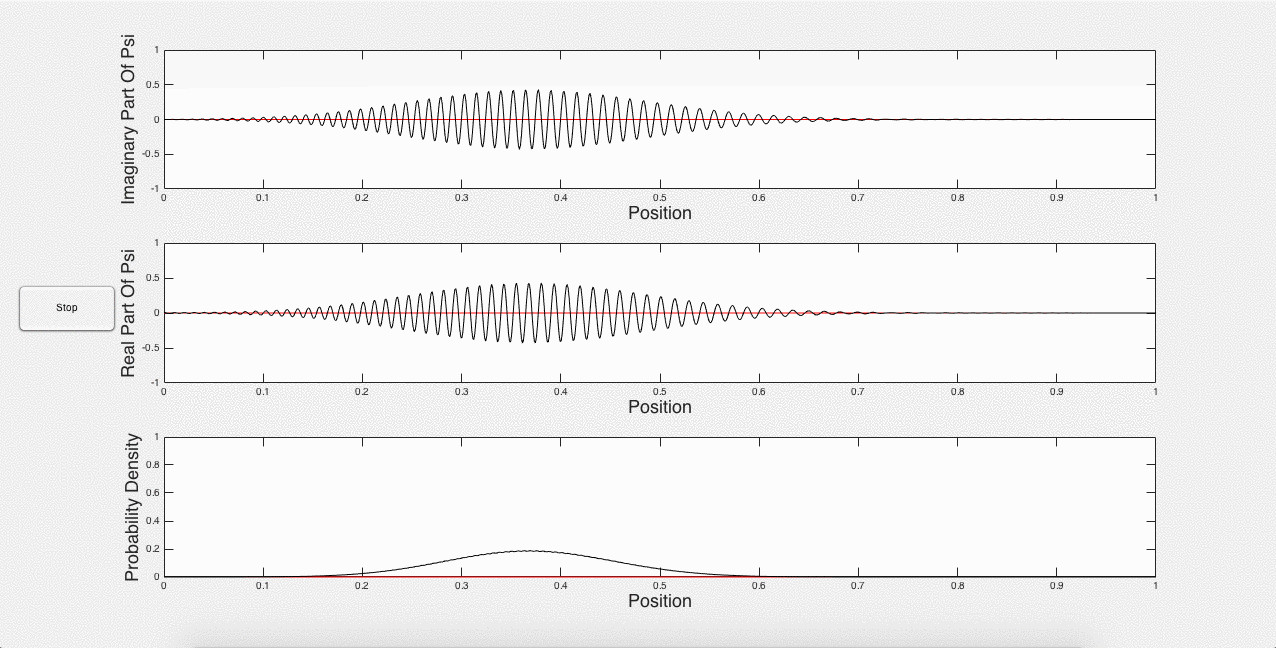
Fig. 4: Spreading of the Gaussian wave packet
Sawada et. al. (2) explain that a Gaussian wave packet is the sum of a few Gaussian curves. These Gaussian curves all have different momenta and velocities. Therefore over time, the Gaussian wave packet develops to show these different velocities, which is the cause of the spreading. Although a pitfall of the model used here, it works well, as this wave packet can be thought of as a superposition of quantum states decaying to the ground state. This is not what is really happening mathematically, but it does still work for the program. It can also be thought of as a formulation of the Heisenberg uncertainty principle, in that we are initially containing the wave packet to a defined space, and therefore there must be uncertainty in its momentum, which is the compositional Gaussian curves (1). Thus, it makes sense that the wave packet should spread out. Nevertheless, the spreading wave packet means that the simulation cannot run for too long without becoming meaningless – the most useful simulation comes in the beginning.
Further examination of the wave packets produced by different energies shows that the wave packets that have less energy have fewer peaks, and wave packets with large energies have many peaks. The nature of the compositional Gaussian curves is shown here, as the high energy wave packets are composed of more Gaussian curves, with each of those curves having its own energy. It is also noted that the high energy wave packets travel faster than the low energy wave packets, as expected.
Conclusion:
This program can be developed much further to include different types of potential barriers. The one used here is essentially a delta function, however it was finite in the program, as MATLAB cannot plot delta functions. However nothing prevents the program from being expanded to include step potentials and the like. There range of possible values for the strength of the potential barrier and the energy of the wave packet could also be expanded.
A natural extension to understanding the spreading of the Gaussian wave packet could be to perform Fourier transformations on the wave packet to parse out the composition of the wave packet. The spreading of the wave packet has been analyzed by Pan (3) using the “Bohmian Model.” The crucial assumption that the Bohmian model makes is that the wave packet has a definite location. This assumption, of course, contradicts Heisenberg’s uncertainty principle. However, the Bohmian model provides new inside into understanding the spreading of the Gaussian wave packet. Thus in the future, this program could potentially not only model a quantum object, but also describe mathematically and visually how the wave packet spreads out using the Bohmian model.
Bibliography:
(1) Giordano, Nicholas J. Computational Physics. Upper Saddle River, NJ: Prentice Hall, 2006. Print.
(2) Sawada, Shin-Ichi, Robert Heather, Bret Jackson, and Horia Metiu. “A Strategy for Time Dependent Quantum Mechanical Calculations Using a Gaussian Wave Packet Representation of the Wave Function.” The Journal of Chemical Physics 83.6 (1985): 3009. Web.
(3) Pan, Alok Kumar. “Understanding the Spreading of a Gaussian Wave Packet Using the Bohmian Machinery.” Pramana 74.6 (2010): 867-874. Web.

