Preliminary Results

I modeled the effect of $\bigtriangleup k$ using the equation:

(1)   \begin{equation*} I_{3} = \frac{512\pi^{5}d^{2}I_{1}I_{2}}{n_{1}n_{2}n_{3}\lambda^{2}_{3}c}L^{2}\frac{\sin^{2}(\frac{\bigtriangleup kL}{2})}{(\frac{\bigtriangleup kL}{2})^{2}} \end{equation*}

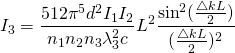
2.2.20 Nonlinear optics Robert W.Boyd

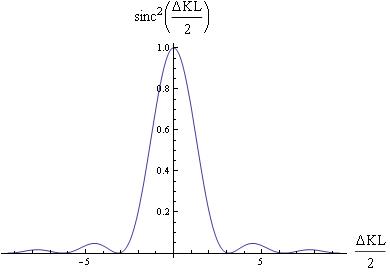
This can be simplified to $I_{3} = I_{3}(max)\frac{\sin^{2}(\frac{\bigtriangleup kL}{2})}{(\frac{\bigtriangleup kL}{2})^{2}}$

Fig 2.2.2 Nonlinear optics Robert W.Boyd

Link to mathematica code https://vspace.vassar.edu/tasanda/sinc.nb

It shows the harmonic generation output as a function of the phase match $\bigtriangleup k$ when $\bigtriangleup k \sim 0$

Link to mathematica code https://vspace.vassar.edu/tasanda/Manipulation.nb

This model shows the effect of superposition of waves and explains why intensity is largest when $\bigtriangleup k=0$

Deriving Efficiency

Solving the general wave equations for the two frequencies $\omega_{1}$(incident) and $\omega_{2}$(Second harmonic) we obtain coupled-amplitude equations.

(2)   \begin{equation*} \frac{dA_{1}}{dz}= \frac{8 \pi id \omega^{2}_{1}}{k_{1}c^{2}}A_{1}A_{2}e^{i\bigtriangleup kz} \end{equation*}

(3)   \begin{equation*} \frac{dA_{2}}{dz}= \frac{4 \pi id \omega^{2}_{2}}{k_{2}c^{2}}A^{2}_{1}e^{i\bigtriangleup kz} \end{equation*}

2.6.10, 2.6.11 Nonlinear optics Robert W.Boyd

Where $\bigtriangleup k = 2K_{1}-k_{2}$ is the wave vector mismatch. Integrating these equations gives us

$A_{1}=(\frac{2\pi I}{n_{1}c}) u_{1}e^{i\phi_{1}},       A_{2}=(\frac{2\pi I}{n_{2}c})u_{2}e^{i\phi_{2}$

2.6.13, 2.6.14 Nonlinear optics Robert W.Boyd

The new field amplitudes $u_{1}$ and  $u_{2}$ are defined such that $u_{1}(z)^{2} + u_{2}(z)^{2} = 1$(conserved normalized quantity). Next we introduce a normalized distance parameter

$\zeta=\frac{z}{l}$     where      $l=(\frac{n^{2}_{1}n_{2}c^{3}}{2\pi I})^{\frac{1}{2}}\frac{1}{8\pi \omega_{1} d}$

2.6.18, 2.6.19 Nonlinear optics Robert W.Boyd

$l$ is the distance over which the fields exchange energy.

$\frac{du_{1}}{d\zeta}=u_{1}u_{2}sin\theta$ and $\frac{du_{2}}{d\zeta}=-u^{2}_{1}sin\theta$.

2.6.22, 2.6.23 Nonlinear optics Robert W.Boyd

If we assume $cos\theta=0$ and  $sin\theta=-1$ the equations simplify to  $\frac{du_{1}}{d\zeta}=-u_{1}u_{2}$   and   $\frac{du_{2}}{d\zeta}=u^{2}_{1}$

2.6.31, 2.6.32 Nonlinear optics Robert W.Boyd

The second equation can be written as $\frac{du_{2}}{d\zeta}=1-u^{2}_{2}$(from conservation).

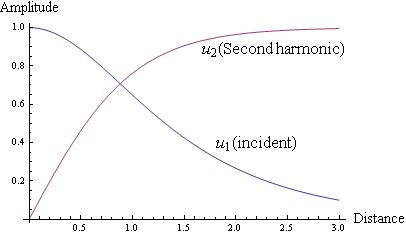
Hence $u_{2}=tanh(\zeta+ \zeta_{0})$. Initially we assume there is only the incident beam and no harmonic generation hence $u_{1}(0)=1, u_{2}(0)=0$. Therefore $u_{2}= tanh\zeta$ and  $u_{1}=sech\zeta$. Plotting these two equations below shows that incident waves are converted into the second harmonic.

Fig 2.6.3 Nonlinear optics Robert W.Boyd

Link to mathematica code https://vspace.vassar.edu/tasanda/u1u2.nb

The efficeincy $\eta$ for the conversion of power from incident wave $\omega_1$ to $\omega_{2}$ is

(4)   \begin{equation*} \eta= \frac{u^{2}_{2}(L)}{u^{2}_{1}(0)} \end{equation*}

2.6.43 Nonlinear optics Robert W.Boyd

From the diagram it seems like increasing the medium length will increase the amplitude but doing so is not practical. Generally a higher pump intensity leads to a larger $\eta$ except to the limit of very high conversion efficiency.

Taking an example of a medium of 1cm length, the efficiency equals $tanh^{2}(1)$ which is $58\%$

 

Share

1 thought on “Preliminary Results”

  1. joandrade

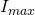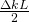    Your graph showing the relationship between I_{max} and \frac{\Delta k L}{2} is quite clear! It’s good that the graph is simple enough for anyone to read, and that the expected outcome (that 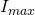I_{max} peaks when 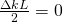\frac{\Delta k L}{2}=0) is what we’d expect, just from knowing about perfect constructive interference from introductory physics! When you inserted your equation for intensity into Mathematica, I noticed that the 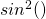sin^{2}() term was replaced with 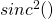sinc^{2}(); is this a typographical error, or is it actually a function different from a normal sine function (like hyperbolic sine, for example)? Although your graph of intensity shows a clear trend on its own, you could comment on why the intensity periodically increases and decreases as the difference in wave vector 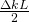\frac{\Delta k L}{2} deviates from zero. Additionally, in the graph of the conversion of incident waves to the second harmonic waves, is there a reason why the rate of increase of the second harmonic is greater than the rate of decrease of the incident? Why doesn’t total amplitude have to be conserved; or even, is it not supposed to be conserved?

Comments are closed.