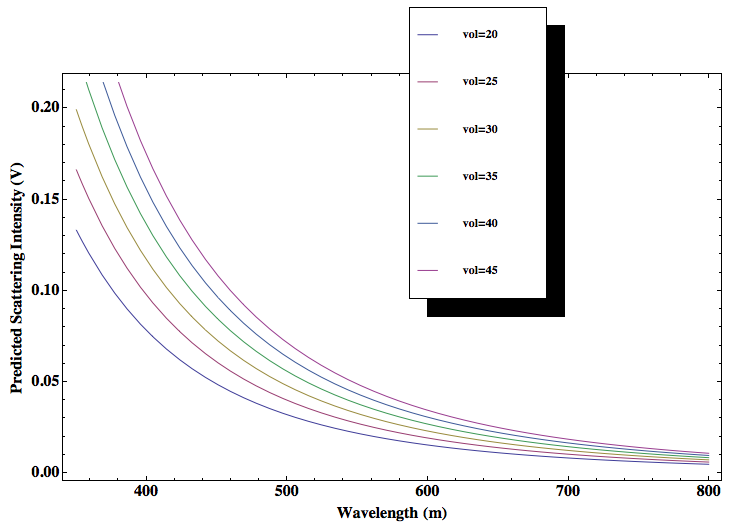
Graph of Predicted Scattering Intensity vs. Wavelength (for different particle concentrations)

Equation [3] was used in order to predict the scattering intensity as a function of wavelength (within the visible spectrum) for different volumes, or concentrations, of particles.

The diameter of the particle used to create this graph was 105 nm.  In order to determine the refractive index of the particles used I looked at the refractive index of polylatex microspheres that I have previously worked with in the VAOL lab.  The refractive index of these microspheres was 1.59.  The refractive index of water is 1.33.  The length of the cuvette was also determined from previous lab work and was approximately 1 cm.  The incident intensity was also taken from experimental data and the value used was 0.365 Volts.  The volume of particles used ranged from a “dropsize” of 20 microliters to 45 microliters in 5 microliter increments.

As shown in the graph above, the predicted scattering intensity increasing as concentration of the particles increases.  This makes sense because as the number of particles in the cuvette increases show does the chance that the light will interact with a particle(s) resulting in more scattering.   From this graph it also appears that light is scattered more (at 90 degree side scattering) for shorter wavelengths.  This result is consistent with Rayleigh theory.  (And also explains why the sky is blue!  Longer wavelengths mostly pass right through the atmosphere, but shorter wavelengths–like blue light–are scattered in every direction.  So no matter what direction you look some scattered blue light reaches your eyes!)

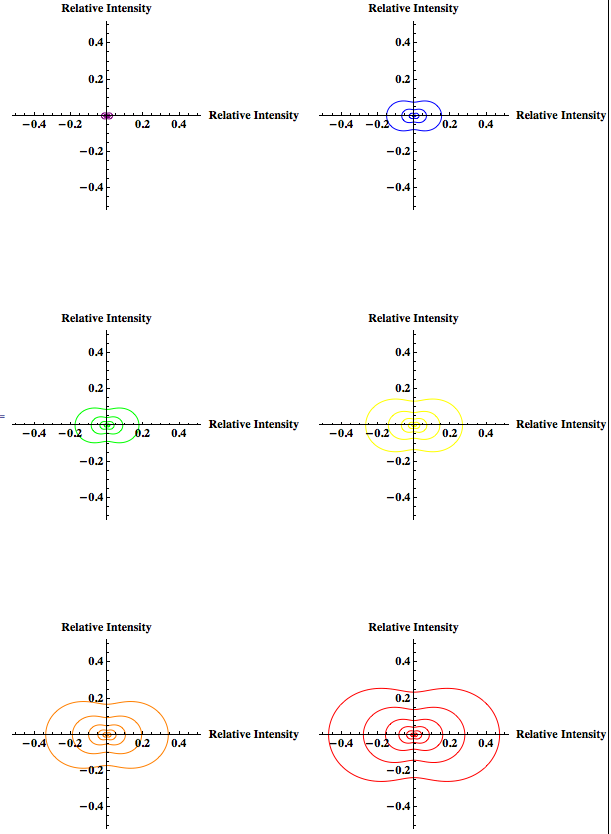
Polar Plot depicting the Rayleigh Relative Scattering Intensity for scattering angles from 0 to 360 degrees as Particle Size increased (for wavelengths within the visible spectrum and particles within the Rayleigh limit)

The color of the plot shows the color of the light (wavelength) used.  The particle sizes used depended on the wavelength of light used (since Rayleigh scattering is wavelength dependent and for longer wavelengths larger particles can be used within the Rayleigh limit).  A volume of 200 microliters was used.  The cuvette length, incident intensity, refractive index of the particle, and the refractive index of water were all kept the same as for the graph above.

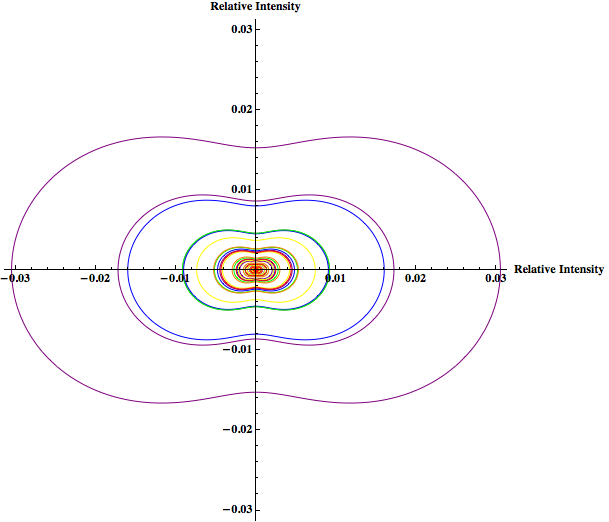
The graph (below) is a composite image of the polar plots for the different wavelengths (above).

These graphs show that larger particles scatter more light.  That is why the purple and blue  wavelengths have such a small scattering intensity when compared with the orange and red, even though purple and blue wavelengths should be scattered more.  The particle sizes for these wavelengths, however, had to be smaller than for red or orange because Rayleigh scattering is wavelength dependent and can only accurately predict scattering intensities for particles less than one-tenth the wavelength of light.

Since the graph above can be misleading because it may make it appear that longer wavelengths (like red) are scattered more than shorter wavelengths (like purple) for Rayleigh scattering, even though (as I said above) the reason is due to particle size and the Rayleigh limit being larger for longer wavelength, I’ve included a graphs (below) of Rayleigh scattering that are identical to graphs above except the particle sizes were held constant for all the wavelengths.

These graphs show that for Rayleigh scattering shorter wavelengths are scattered more than longer wavelengths and that larger particles produce more scattering.

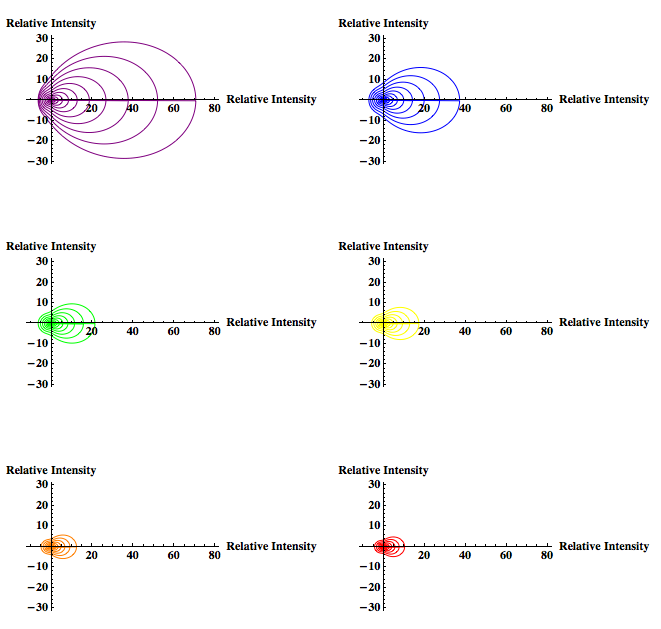
Polar Plot depicting the Rayleigh-Debye Relative Scattering Intensity for scattering angles from 0 to 360 degrees as Particle Size increased (for wavelengths within the visible spectrum and particles greater than the Rayleigh limit)

The color of the plot shows the color of the light (wavelength) used.  The particle sizes used were the same for every wavelength.  The size ranged from 100 to 200 nanometers in increments of 10 nanometers.  A volume of 200 microliters was used.  The cuvette length, incident intensity, refractive index of the particle, and the refractive index of water were all kept the same.

The graph (below) is a composite image of the polar plots for the different wavelengths (above).

These graphs show that shorter wavelengths scatter more light (as expected) when the particle size range for each wavelength is identical.  These graphs also show that for Rayleigh-Debye scattering most of the light is scattered in the forward direction.