This is the mathematica file for the first mathematica worksheet.
This is the mathematica file for a delta function potential. Edit 2/15: Delta Function File has been updated.
Project Proposal
My proposal is to work off the existing research that was performed by Jenny Magnes, Kathleen M. Raley-Susman, Alicia Sampson, Margo Kinneberg, Rahul Khakurel, and Rebecca Eells to model an orientation for an organism, specifically the C. elegans or nemotodes. The existing research has shown these organisms in certain positions, such as almost overlapping or orthogonal, so by using their existing research into the ways light diffracts off of these organisms, I can model a different shape or size using Matlab, which would permit me to add to this body of research. This project will specifically model physical size of the organisms using diffraction.
Quantum Cryptography Assignment
This is an encrypted message using quantum cryptography. On the “key” page is a demo of what happens when there is an eavesdropper.
Wave Interference Assignment
This is the mathematica file for the wave interference assignment
This is the mathematica file for the Fourier Transform assignment.
Diffraction Models
This project involves taking the Fourier Transform of a mathematical function that represents a small, thin organism(s) and determining what diffraction pattern one would see, should a light source, such as a laser, pass around the organism(s). This modeling builds off of the research performed by Jenny Magnes, Kathleen M. Raley-Susman, Alicia Sampson, Margo Kinneberg, Rahul Khakurel, Rebecca Eells in 2009. Magnes et al. worked with C. elegans, which have a thickness similar to a single hair, and passed laser light around the C. elegans, which produced diffraction patterns. Due to the size of these organisms, it is impossible to see with the naked eye the number or orientation of the C. elegans.
Our first question is “what is diffraction?” When light interacts with an obstacle, light will appear to bend around it and will produce a pattern. When light passes through a small slit whose size is on the same order of magnitude as the wavelength of the light, the effects of diffraction are more pronounced. For this project, light will be passing around C. elegans and it is necessary to determine how the C. elegans are aligned when the light interacted with them. Mathematically, it is possible to determine what a diffraction pattern would look like when light interacts with the C. elegans. To do this, we will use Fourier Transforms.
Fourier Transforms come from the idea that any given function can be created as a sum of sines and cosines. The basic Fourier Transform equation is
![]()
where f(ξ) is our normal function and f(x) is a sum of sines and cosines.
Why do we use Fourier Transforms? Fourier Transforms are mathematically equal, to a certain approximation, to Fraunhofer Diffraction (Rodenburg). Fraunhofer Diffraction is also known as far-field diffraction. Fraunhofer diffraction occurs when light passes through a slit and causes only the size of an observed aperture image to change due to the distant location of observation, and the planar nature of outgoing diffracted waves passing through the aperture. The equations for Fraunhofer diffraction can be applied when a^2/Lλ much smaller than 1, where a is the size of the aperture, L is the length from the aperture to the screen, and λ is the wavelength of the light source.
In order to use Fourier Transforms, we first need a function to use. In this first example, a function that defines a rectangle was used.
By taking the Fourier Transform of a shape like this rectangle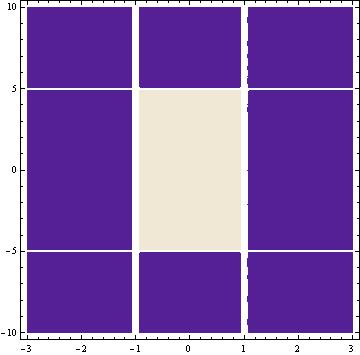 we get this
we get this
If the pattern of light seen by the researchers looks similar to the Fourier Transform of the rectangle, then it is likely that the C. elegans were positioned such that there was a single C. elegan who is extended. The size and number of rectangles can be changed in the modeling program, which permits researchers to adjust the equations until a diffraction pattern is created that looks similar to experimental data.
Magnes et al.’s research was produced using MatLab, so this project worked to create various shapes in mathematica to further future research. In my modeling efforts I created the following shapes: A single rectangle, which you can see above. Here is the mathematica file for it.
A pair of rectangles: The rectangles were created using this mathematica code.
This graph is of the two rectangles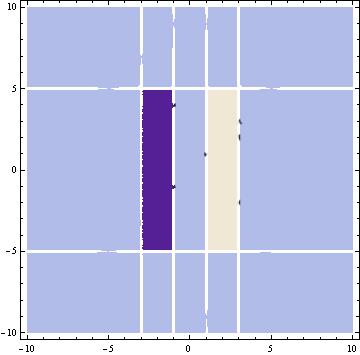
This is the Fourier Transform of those two rectangles 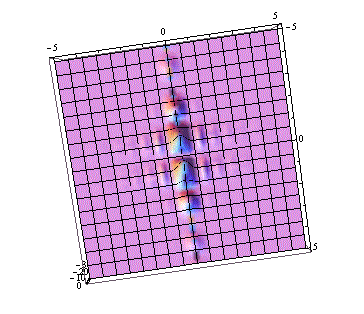
I was also able to create a Cross, which was made of two intersecting rectangles. This is the mathematica file for the Cross.
This is the graph of the Cross: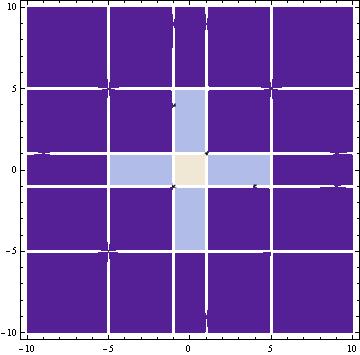
This is the Fourier Transform of that Cross: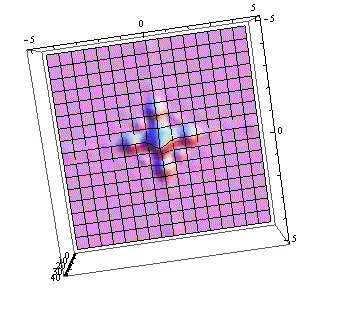
I also created shapes that were asymmetric.This is a .pdf with two rectangles off center from each other.
While this is the transform and this is the mathematica file for it.
The successful shapes were created using sums of Unit Step functions. These functions are 0 when the argument is less than 0, and 1 when the argument is greater than or equal to zero.
Problems arose in my attempts to create shapes that were angled, or non-rectangular. Shapes that were angled were difficult to create, and anything that resembled them created Fourier Transforms that were imaginary, making it impossible to graph. However, despite this problem, the results obtained permit research into microscopic organisms using diffraction to now use mathematica to attempt analysis. The plots of these shapes have whitelines throughout them. These lines appear to be a product of mathematica and do not impact the project.
As a result of this research, I have realized the complexity and difficulties that are innate to understanding microscopic structures. We cannot see them with our naked eyes, which means we have to rely on elaborate ways “seeing” these structures. This procedures require a lot of fine tuning and models, and we have to take each structure on a case by case basis, which is astounding.
Citation
The Fourier Transform. John Rodenburg. http://www.rodenburg.org/theory/y1300.html
GraphicsBox[GraphicsComplexBox[CompressedData["
1:eJxlnXmAj9X6wC1jDDMYM2MfO4WLq3LdXzW8b6FCcVPhNqW6pWSNkEqlha64
kihbQipZKrIV9b6WdF3iWrMluywzzNjG/pt5n/N5vvec+mf69JzznOc557xn
fc63mv/o27FbkUKFCk0vUahQwV/5JyGUv3XCum3G1mkzNk65bQHWKaz86+Le
uxf3vhzAN0TpzyrvjeQnlPdHvFtZ/i5dDm8TuQfvkPzKtUW/8i4pX/kesc+3
08cpG/9cDqNkdWqqvzD+wvgL4y+MvzD+wvgL4y+MvzD+wvgL46+dPs63y0tw
OawT/Yd09RfGXxh/YfyF8RfGXxh/YfyF8RfGXxh/Yfy108f5dnkJLodSbHn1
F8ZfGH9h/IXxF8ZfGH9h/IXxF8ZfGH9h/LXTx/l2eQkum3xl1V8Yf2H8hfEX
xl8Yf2H8hfEXxl8Yf2H8hfHXTh/n2+UluBwujIqNV39h/IXxF8ZfGH9h/IXx
F8ZfGH9h/IXxF8ZfO32cb5eX4HI4P+LzAf7C+AvjL4y/MP7C+AvjL4y/MP7C
+AvjL4y/dvo43y4vwWXj944Mez7akWHPRzsy7PloR4Y9H+3IsOejHRn2fLQj
A39hez7akWHPRzsy7PloR4Y9H+3IsOcj0scp46/D4ffiv4e/MP7C+AvjL4y/
MP7C+AvjL4y/MP7C+Avjr50+zrfLS3A5/E76t4+/MP7C+AvjL4y/MP7C+Avj
L4y/MP7C+Avjr50+zrfLS3A5bCfjl/oL4y+MvzD+wvgL4y+MvzD+wvgL4y+M
vzD+2unjfLu8BJfDb2V+Un9h/IXxF8ZfGH9h/IXxF8ZfGH9h/IXxF8ZfO32c
b5eX4HJ4o6w/1F8Yf2H8hfEXxl8Yf2H8hfEXxl8Yf2H8hfHXTh/n2+UluGzm
2ZrqL4y/MP7C+AvjL4y/MP7C+AvjL4y/MP7C+Gunj/Pt8hJcDuVvHd/ZH/nO
/sh39ke+sz/ynf2R7+yP1F/Y2R/5zv7Id/ZHvrM/8p39ke/sj9RfOEreJt7s
B2qF+A8bue/IlaU+coLI6sWVlMWN8uY7OKTyo5FgnfJGYQ+uKemVyV8r+puk
+WHyw+SHpT5ylGUPnKf5sRemvWDqH752veCfC3/Qd5f1HeQoYz+MfTD2weiH
0T8nqpAjAfph9MPoh9EPox9G/yphD/0w+mH0w+iH0Q+j/17rO8xRRj+Mfhj9
MPph9NeT9lD9MPpdOfMX/Qk5/QnGHhh7YOxxy3tO+q/qh9EPox9GP8z3KeNQ
LR2fYL5Pl93v23DoyLV/8r1iL4y9MPa63zf7NfLD5IfJb+8Hc5QZP/m+GO9g
5HwffK8w3ytMfpj89H/yw+SHyQ+Tn/5Nfpj8MPlh8tN/yQ+THyY/TH76G/nd
/uf2b5j2cNeHbn9314uuftZD6IfRD6PPXm/lKDv9U+cn+jPfq32+kRPY++sc
zz4PyAns/WiOZ++fc3Q/iBxGbu93cjx7f5YT2PuDHM9l6k/abb85L0sJz0T1
s0y5WvR3qwfLd5Xr9Yy+/xLKku5KAH8c/d2u3MGUCxeN/OEcKdf7LfqXMmqP
9JtyPvbA2ANfica3o8pLRV/g2iv9MkX1y7qkXNhA9ClTnitH3yqRe8ixB0ZO
evmu96scRo69O8V/ZeoXvhr5WVTZrW9X3tL0A9htD1e+UeQe7LaXK5d6uaLs
tqcr7yf+aP3THtQvTP27ctqX+kVO/cPISY89lE/9k57+AyMnf/Sf6xQ381Jt
cw5f3IfJT/vKfP+7tidyl+nvMN+jU57vlKfzK+VTnls+/Qv9bn+jfNLjL0x9
UD7zMfWJP6R39bnjN3L8c8dTx19dDzhyPQ/tLeuPkP4k8orKzP+Sf+ly0tO/
SA+Tnv0N6elfpIdJz/xGfeAvzHzE+E/98L2SH2Y+Ij3thxz9MPqZP9DP941+
GP2kRz9y9MPoZ/5BP+MB+mH0kx79yNEPo5/5C/2MH+iH0U969CNHP4x+5j/0
Mx6gH6Z/sZ6gP7nzk3u+RXr6E+lh9/yL9PQn0sOkx1/sx1/sxV/YGR/c71fn
f/o3TH+278NStL8yH1FfMPbA5IdZj+Af+Skf/XxfMPYw/iOHkTPeI4eRM54j
h5HjvzueMb9iL4y/MP7C5Ge+JT9Mfpj8MPmZf8kPkx8mP0x+5mPyw+SHye+m
p72ob5fpn9Q3chg59Y0cducH+gP20V4w+yOY/Q7M/gVmPwLzvTH/Mb/RP9nP
wqz/me/c9RzfG98nTHrmY+rT3V/jD+MBjH7Gd9LjL+lh0jNek576ID1MesZf
0lNfpIdJz3jKeQLtBfM9jYkq6rz6T/278yVyxluY8RTGHpj+4tYv7Yk+GH0w
+tz2h5kv0M/+Eaa+YNofZjyhv6AP/eiD0Qejz96vZAXjIoWpfo+o3o95vaK/
aSFyWPrZMU0v7Zel6ak/9Mu8ckDzN4n++2pl6VebNP/oSO8RZfx1x3vGU5j+
THqXGT9JT39G7jLjJenpz8hdZnwkPf0ZucuMh6Tn+5Z6PaL1S/3B1B9M/cHo
Rx/M+Ej9kp7y3fp168utD9df/JGF8F5t33hZpyknLilIMEd5TmTXHG3vS1G7
/aL8tehTRj/2ox9GP4x+GP0w+t3+D9PfKZ/xBmY+JD3th1zqaZNyRWk/zS/r
8AOemx59pIdJ77a3O16hj/EKZryCGa/c7xdGH+WhD0YfjD6Y8Ql9jE8w4xPM
+ASTH33kh8kPkx+mfezxbL8y6w2Y9TTMegNm/Qwzf7n6KR/9MPph9MPot8fX
/cr0P7f93fnGXk9kaXraF2Z8l3SJOt7LPJugLO16PYC7R/5eVG5u/IbfjrrB
GmUZt056sHy3Z5Vl/VRE7ZF+V0xZ1lVldb5x7ZP+n6wsfhZT/1127Zdx4UyA
3GXXn6PCHnKXXf8GSHkqd9n19wPxT/11We5dk5XxH5bPsKzWR1xkT2nV7+an
fhn/xkr/MN/jcdGXmRZ+E6X7XZn8pH83+nvyD3JZx5VSlvuMIsoyzp3U+n7I
9HtYxp3ryuJHotrv9l/Kg93y3P7slu/2Z9cetz+79rn92bWX9mB843tl/qA+
mf9hxj/SM18gZ30AMz6SnvkEOesHu70PaXrmG+SsH2Ds53wP+2XeTNP1C4z9
pMd+5NgPYz/psR859sPYT3rsR479MPMb6Wkv5OznmF8ZX935lvoiP/XD+gF9
dvxwiq5nSM96BmZ+JT3rG+Ssb2A7/jhF11PIWe/A2IP/2IO92ANjD+mxBzn2
wNhDeuxBjj0w8xPpGY+QU59u/3O/D7f/u/3bze/2T7f/uf0LtscX4iGyzXls
bDyy4xmyzfxUSOV2PEJ2cDaqp4M6/tjxBNnBS6Ze7PGFeIBscx5ZWO3jPAR5
9HdobD7lPPj0zB5/KXEpy5sblB58x4fF1T77fDnb+BOv4ynnveSfXvbOW8s9
kKf22+fH2cH2yP9zOt5Kv9qRQf7PWvS4YfBLSzQ/cvJX6BNVgI63nNfmmPwb
1g5ouubJc1o/9vlvdjAhav88zc/5J+WvqjLr3MTq8Vp/9vlutlmvFNf6o34p
v8Oxd7rPWhObX7m/RX/r23+oP+SN2PzM+RH6Zb4vpd+D3X+Pi76Zqc58mqT6
q0z+8XB6+9h8S/9D7h3qXPLpfYVVTv9DPnTRrGXL/3NM24f+h38H6pZeUO3k
QWc+Lqz118nPefuH7oV8ez5MUnmTC12fHLg9Uc+zqL+o21/P0fUN61sYOesV
5DD16a5/qH/q970CXJus903Yh37mZ5j9M+dR2Mt5lCunvyBnPw5T3qIo3TVl
4tngXmadiH4YfeSn/mH7Pv6qpieewZ3PZL6o5ZwvxeLbouy9q6scRi7jdXVt
Dxg58QzIYUl3OGC9KOPqQeWVkR8blJOidvm3soyTP+l6c7akV5b546CyfE+H
lSm/nXxPPuXDlA9TPkz5MOXDlA9TPkx/YP82PuKTqp/+CiPHfvM9BldmTdx3
7FH2y8c1vZwz/64s5zQHNL+sa1coy3y8WeundSQ/qiz9/ugf9MHog9EHow9u
H/GvWr74t09Z9kk7lWXc3q58e7T+mKycEfm/UPnl6F8mq/1JIleWfeBO5VGi
X/lOsU9Z9jf7lLHfbp99ytgPYz+M/TD2w9iv/c/YD2M/jP0w9sPYDzOfwOzv
YPoT/tKf3P4Ay/pxs7Lso1Zofcm57H7PTU95pIdJD1vv0zLT7PdpmbHzLdh6
n5aZZr9Py4ydb6Hfel8wM3a+BVvvC2bGzrfQZ8UPZqbZ8YOZaXb8YGbsfAt9
VrzazFQ7Xm1mqh2fNjN2Xok+a/+fz+zHYPZjMPsvmP0XzH4LZr8Fs7+C2V+5
5WMv5cOUD1M+TPkw5cOUD1M+bK1//4ft+eaYytn/IGf/A7PfgdnvwOxv7PF0
r9Pf92p56IfRD6MfRr89vu79Q3+w57Njaq8d/1dHOapmfW+b47w3ztH3uPZ6
Id1ZL8Tet7rnkfb7ixx9j4Hcfq+Qo+8XHHt9xz5dn3H+yvqI8vneuR+17gsz
Y+f39nybp/slyXdR79OkP59XJh4VpnzWV8Jn1D7Wh248FfZY8UWZaXY8Qmaa
HU+UmWbHI2Sm2fFDmbHzaVc//lr37TNT7XiSman2ffvMVDt+ZGbsfBq24s1m
xs6n8b9w5G+unq/Tvm79UJ+cv3AeQH73/gqW4TlXzw/oH+55uR2PlufEi+Rp
/AftT3vR/m77or+v8B/sozzKd+9POU/g/NReL55w5u+Tuv+j/2EP5VOf1B/9
GTn7JepzrNgT2vu58rqfYf/EelW+9xTn/quib98XVVR/2U/Z8Repep6MP9Qv
+x3Yfi94Tu2nvfi+qQ8Y/7GH8V/SVVC2/cmW/tAsRfurW1/2958j5+lZsfHO
Tc/+Fbm7n6U+qC8YOefH9nuQRB3vqT/xI0e/d9qP+mB8hvleqB/GL+qD/G57
E7/C/EJ92ufB1ZUZ7ymP/oR/3F/Y95nJKpd8ZZ14srLav9kvU9/0N+obpnzO
S9DPfQH6YdJzfkJ67hPs91VFND3nKaTnfoH0MOk5XyE99w2kh0nPfp/03D+Q
HqZ+OL+jfrg/o35g0nNeR3ruy0gPk17m4x0ZpOe+jPQw6TmPIz33ZaSHSc95
Bum5L7PH12LavvhL/eAf9eP6S39EP/3PPu9PVjn3ichhyoMpD8Y+6pf01Cfp
YcrjPpLyYPLD5Icpj/YhPe1BepjyuM+kPJj8MPlhyqN9SU97kh6mPO5DKQ8m
P0x+mPLoH6SnP9jzfTHtP9ynUh5Mfpj8rpz7Rvv9YqL2J8YXymM8oTyY9Iwv
pGc8sd9nFtH+xf0l5cPoY/xBH+MN+mD0cd+JPhh9jE/oYzxCH4w+7kfRB6OP
8Qt9jFfog9HHfar9/rCI5mc+tN9XJqqc9rHfpyZqfVN/yGHk1AdyGDn+IYeR
Y6/9PrOIsx5J0fM+1hPkZ76z3xeX1fmZ+Zj1GetNmPkdffbvLZj189rYeoTz
YtYToq+kyokXQx/xeMiJH4OJH4OJH4OJH7P7f+z7cb8Pt3+7/ZP+xXkO6x32
P/K3itZ3X1nv6fqH+qN+Yfv+urpv359WV/2it5qud5lfrPOa3bH1NP6zPoPZ
XzB+2b+vFHtvyvqK/RzlYz/zIeXRfqyfsY/1Nu3JehpGH/MX+mhv5Mw3yGl/
5MwPyOkP+Mv3QX0x/1rr3f/Zj2AfTPwnTHwnTPwmTHwmTP+Rcs+pPcjd9+/U
L/VH/ZKe/gvTf2H6L/c36Oc+CKZ/op/2sd/zXdPvh99ngNnPUl+Uh32UB1Me
7Ut67Cc9THram/T4R3qY9LQ//Z/2oP6ZD0iP/dQ37Y3cZdofpv2xz36PffUP
+mlf0tvvb69qecjt97dXtXzkfB/IseeZp4a+8vnFLD2PM6znccjl+y9v9ntx
4dZxT+xa5nP+nRA27Dm1bqsg1bwnLKxy6h/m9zJgfi/D0ad8gynP6Pcpz8j1
90GQUx5MeTDlOfqU8fcGM77BnA/Cpn78RQ+vrPN77fhwf9x/pp5ekRru/OTB
NjctLqJ8aefPu8+OuRbA4/76jzqzCxX14T7ZG68/3ideGX3VL//liTIt0vzt
Rh+cZ/RVM/zB4c6Xhy+6EDzcc/+bBdy38LH3jtS97pH+Q1Me3M+UR/6da+bf
eFv57GDrhzUqfz+oil+/1vr7EvvmBAcu7CvQF06vLVz1YsT+9PN7RrQan+Ml
dX66evkZqf579VpW6Xz1YNAiT9KP3fpK49tvPBz4u399ucCfEU1vWpxdaa3K
px2qUvS1FT8HnpE3vnV2oXz2kFcdEXyTn94j/5Jn9zfK16fyb77/rHJ+eR75
65vxaHvfIblN8/sf89W8b4Sxb1Xx6kPy0/ujjX0r69R6q8Cft419K418jLFv
hZFjH/KGxj7yJw8Z8/YXV097Gzac3t/3/iQ/8cINJw+cPe0dajc6WLk/yV9q
7Cc/9pP/gNgblG7/Zql1+f156IHpNUctuuBVGjt/zdn89IOrdt37fNs85WFG
fqR3+1sT8/Ov/nOpZg2Lxn7PAWZ9dsSsF3qOvThl2fLU8N4NOx782l+1HN4i
cg8mP+MN/LUZX2DGE5j5FWZ/BLP+O27smdg7/slWLdP8gW/3HnV14drl8AZj
D7zNtCf1MztlQdRf7/38yzI3ZZYM4YP7Xu9+dtfVAF68fuKaytd2B3MMlz73
bMkNS055swxXb5rQdXZmUX/LkuPV/3v32eBAfNQ+4cTSIl/bZPS55w+laHzN
rseKL5+2rpzGk/Qf8ebc4pcTwi+Mvq4rFrSIL5EcUt6+dRemPzQzjvtyr9iX
61s0bFVU42Eaf/qnGdMrX1b7SjZI+1fz3rkaD/PZnpf/te3vp5T3/urP23jl
vwHl/VC66ufh0k0aHzP66sAw8bs9nsbbNBu57tYpuR76n5o/Y99HbS6rvHJW
3menS1zT/Ffvv2XFlmVxPvrfLROsG5ZSQv3v0eh446/6l/S7F//t9Ny4bC85
fl+PTsnJWh+Hnrqt8sH5pcN9pj+fnS/fH/nrTctr+VjT2PvtKUNfjeTYd/X4
wFufWFvaf2Ha4fcL5h/RUwbW9QNyh3U+Rn7NZn1/g9xhfW+DfIPN+r4GucNB
f7N/QQ5r+5Xaeml9mXJqn8yjKWof6ynkvQyb70fPp5l/JBytkn6fu5z6YP2E
PoeDqWa9hNxhfW+D/G826/sb5A6b/Ynaa/ypFNYz43WDMfZ4Z8azcIAZ7+DX
jbyijH/hBvlePb5X6oP91idPny7y/Z6zmh859xXYCzMelPtz9L3r91kr90/F
bjmdouOX017mPjEm7+G0F+0BXzH9kfTXHKZ9SE//RH6nw7QX6em/yF2mPUlP
/0XuchHTnqR/zvTnH42c7xO567/rzzTHXteeonZ52j7InfkocOajwJmPAmc+
Cpz5SPcnlOew7v+RO6znAcgdDlaa/QbyVTbreQFyh/V+ATnnNe1MP/AffLXr
h9/qfK33Sfcs+v6t6wezvNfuqdbz6IRU1cf6YK7p7xNu3dJl1WvFdfwdXGzd
pYp18nQ+KjPkYouF7yzU+SZv24n+K8ee8+Dt0w+mVfxrLH51ucSv6ni/UuJh
df563Ivia3X+mSvxusoLJP5X55t7JZ5V7Xt4br3Bz2yOzTd3SzyrP3Lt0YX9
thz3/vnzkpfuzt8vLPx3xrga98d4bI0OJXLH/a7rx/9+98xTx2oeU25v6usV
qS+9j8xpF41PYdlJZwpfKX7S67xW9JX+amqt+96JMfbUk/hSXQ8UK/fOmqnN
Sun6pH7X9BNH/x2Lh20v8aqavulH37VY3etYgP/rJN5V2+MvLa40rtD2kM7X
n0i8rM7v3dc0/DxjaCGtn5YSb+sjb/XKpDfOZCX6ZrzzEsU+f9KAtPOleh7V
9fhKWZ8qL62a/MBb3+5Xvv/mZcndum/R9X17WQ8r1y3RbfwnJUPlMsK6nn9c
1te6fm8p+lS+QMpT+TBZryuPF3uVPzb2s55eZeyHjT7lLsZ++D5jP+v9ZGM/
8osJYj/8iLGf9A8Y+5HPN/Yjf9PYD2M/6Zmf9sh455955oQ340pWUPyGYs/9
MlTX9zp/ffW4yBvsuPRuvddSw8F/emPT6h3H1f6eI08U9He1f1/8rd60d/dp
+5Wf9sFPm1vu0vYp9viz/9do+TaVf5NZdtQNaxYrN+jVr/kdU8dqfb8ucuWs
x6L8yp/83OrUpA/3KO+V8pUPGnuwF3vgC6JP7V9j7IH7G3tI/76xB/kRYw88
3dgD7zf2kJ/5nPPWx6T+NP0gU7/Y38PULzzF7BdGPFHwfSeGkw1/Obtgf1JI
uf3Gopt+X3QwgGsmfTMlt9Bxj/3G4RcLvs/CPlxx+G+H7xxR1kd/+vBurySl
xKu+N6aeajnnnnMB8rvOLG98Y8NvPeQnMn6q36RPnjfJcMeH7j+9YWZxH3nY
pGD/U8r/8QcZLyc1u2fY0iC2/yNeACa+gPHq/wYXnBeUVXuGTH127v4g2fxO
4llv0c3xlQvGT3v+Le9P6VQv2h93WvK3kTd+ViuEm79/fNbz46uHz8v5BOcd
4WQ5v1AeIOcbAZwr5yGcd4Sb5byE845wvpynKPc3+s15iz/R6If7Gf3wWaMf
NucxnNf4C41+eLLxZ8iu06Uuta7uTzV8dteW73u8Wsu/XvTSP29eeFjPQzqM
bhA+9lzs/KTljKTej5zbqDxm3YY2ZY+sUe4nrPNXI0mv3E70KV+U8pQvm/I5
j/ibKR++yZQPjzDlw2+Y8uGapny4rSkfPmfKh1mfc54xqbHMR/e0vW/FxfMV
9PxxkTlvnHhezlMu9Xz02NfflA8X9NuW//2eVHuWe980m14jO5j3a6fsbrNT
/Y9Nf/xLUusnO0xO9fuOfr7jW99mBbnlJT35m5v6uOeDapsLvm/0xV0p9sLP
7WL8i6wXlGveN2rey3cd0PbYueah60NbrFTus2Vl5qD2m7W+67WeMLn83iPK
vX/7WuYro6+xyP+gH95g9MODjX64jtEPv9Ow+cwR839Ve8Tffcov/LL80Kwi
Mf5q4MZ/F4y/8G13TE05VH+n8q4fnsiqsn278rx86z6oNkO51YKzYwrGZ11P
7fvz0p5dFyhPytdWMF7DN0l+5WKSXrmulK98zztN/lownsNrxR7laxcSswvG
d3iI+K/cT/xVHmvqh/qifmDqR+Wmfjg/vNnUD/Ldpn5WGJ5i6gd5DVM/cCNT
P/BIUz9wG1M/cJKpH21vUz/w3aZ+4J9M/cDF8qR+sP9VUz/IqR+4qPR/5fFm
/az90ayftXzz/VC/xc33o/3HfD9wD9P/4Yam/2t7Fj9btmB9Br8k/V152aNn
xhasx+BAvg/l3xYUfO/7ldPle1K+YPRrexv9Op4Y/fAPRj+MfriK0Q9z/sz+
wd6f1nHvM/S+BOb+DHbuL0Ln/sK9j9H7EBh9cB0zP7f7+eLhpv9zP4LcuY/R
+Z/7jp2/3pLfo3O9feZ+4FMZv4PxvaL7g/CRiWWu3ln7slfZjO+M55zPbJL7
Bm+LuW+o8Up0fh70mP9OucLLymt9uedbnB8VNfefT/xjWNeG+fZ3lfICyvtc
5peA+cU+v6jkP27sO2rOh3rcsmnZkbpnWA9qfE3Oa5//b/tpPPFu8T/Af/Qj
32TOk7kvubBH0j9q+gfpicedIvcrHuk3mvMt+OG9Ut8jE6z8ul4tZupj6kcv
Td+Sb6/xL+D861NTH4cNk5/6mPJ7gz6z8k578568/q/LQXm/p6kPs771+wiz
3jXxBjlBcmpGw/Wx/qHxxrTn2Evpt7W9r5xfUu5HgmFfR+3L/UgwrG1ybrHv
Uvyy5v6k2rYtn9eNK+vf3ETso35u6bIif3w66Y3bcSCqj47s15fsH1fxmTQz
fp3U72+ezO/KI+e17Xa5SI5XuWnjzgs+LaPl5Y284809/VL8W8z+nvVv1pey
v59suJfxn/5B+1eV9ghv73jo66euZXn3vJF2MD6zvD/NrG84r+Q8lHgYzs+k
3UqzvsDecJ7Z340av++G1o9U0PV654d+eXtCoxTtb6zHk0x9fvH+jPId7i2r
7cH6HXnWmM9e3nYl2S9h+pvpj/jjpRt/6B9jpf7DFFNfD8Qf/HHRAi1f44Fp
z7V3p3Ue1SNFefK3zw5q8n0Zf2HfLpeHL8rR8fdh8/2Z79M5v05Wlmsgvc/S
eFr7/LSUc35XRJl4M5h4MZj7ffrD+oe6fL3wQgmtP+I1YeIjYeIXYeIL7e+h
mNrr6nP81XhO0rvslk+8JXKXhzv2ES+J/IjDrv3Pm7gF5AMcdvzTeEbkLhP/
Rnqn/QK3/bZK+6j9bnsSD4fcbV/i4ZDT3siJr7HPYxOVXXu3O/a45bvlof8j
8/2eySjY3+h9gcbTTbXvK3S/nynfu85XyBnvH5f5z7xnuEa8g+6f2jrxHDLv
p7tyv8vMn5oMvnTaW1i92vBZj9YKOxu++uSwqQPjqodzOw67c0L++Ll8TZGl
t71aSbna6R61h5yq5Hcy6ZeV6FQxb3t15ff7x686tqaWP8ekn32u7qdfHawd
zjN8+u222Xck1FR9Wx+9a9ex/6T78Iwp1z454Nf0Sd/9jXd7lU6roPKBTff2
mfX39LDk//W77ZdLWfnj19NVFjWtpbyuabm1oxdUC0sYfiH94KC+aTV8uNE7
PzT69VQt/6/fNnzscOls74t6A6uVjE9nvx7kyn49/MjwYNnPhx8bbinnFZq+
s5xnoD8w+sPihgdK+dgX/Cz2afqqYr/fVOwJZoo9oanPwNRnaNorWC71Tf0F
6dIeyqG0F+0bmPZUXiTt7X9p0pv6pX0CU//Kpn1Uf660H+0TfCbtqzxA2sff
VWdR/bTvsrw51U71u8WP3cexHua8mvfknB8RzzH3x1drf5VfHymVOtWoUaJ8
2KHdxOUPLcgKStTq+HTX/PlkRJrMl5df7t7zt5Np4UKzntnyn7qNJs8s49yn
poWLjPzuKYX6x/llNf28199P6JhSPJxq+Lfx7R5u1uZCsMDwY5dL7KnXf3KA
fHTrnqmf9j7vfWT4k7/X7jZiZrx/4zmZ/7Y881uVsyPjw8lyfhGsePrg0Jcy
zgf1jbzfi4WDp/d+4iGfN2DLycdfuuDVM/Ipz/9y/9EGxX3kX7T+YMTGO5NC
1mvNHm07qNHapJD03UbV+7LitkIh9mR+tmfSoMzCKq/b6UTbtz86HODvuO+X
Xb22+GiA/k9eXlfrwUq/e8h3Vb3cd8/1w2pPowk1DiUOKOwjv//VXhfmZRXy
kZfsIPEuyJ881ScIskpo+Re/7uc3r1ZGueqlot2Gf11U7U1JW3r/oWZx2h5l
+xX5d9lCVwPSDx3eMPXjYacD0vf5btzJh8fmqD/9Sk1pNWbsDvXnXyOWjb6t
805tn/SfK9dvV2ebcs0eCz9du/i01n+Vv73zcMZNVz3a91KNWq8PrXPFo75P
nrj7yypri6q/HfcvSHgovqRP/xj807UqF14roe0/Ytt3m594Jub/w80nZT90
5rLat+f+y3unPbZV/UuZmv7asFU5Wt+Hil2Z9GKHOC0v7d5ovaz6urwbred0
fcl8xX3TcInfUDnrD5j5jPPcLhIfovf/rDdg5jv0/1PiT1TOegj+s5kPSZ8m
8S0aP8B6A2a+JP0RiZ9x4gmK6Xm96w/rKZj1E/dl5yS+RccD5LDrL+spxqeb
JZ5G4yWQw8Md/1lvUX7pvVH8jsZTsP6C3fpgvUX5t0m8kKZHbt9faP3oeoz8
QyReSesPObzH7Bewt/tbf2v/Y1qyEy8RY9YvlMf6nPZ7XOKh1B72I4x/t9wV
7Re0fepLfJDaw/4GeU2Jx3Die0ops36EK5j1Isz6EP7NrAfhdmb9R3n/kHgn
1cf3xX3qeYlXUv+xB/+rSHyZyrGP9igl8VdqH+td8l8+G8WraX9i/Yt9XSXe
S/O73+d+iX/T/oT/lB9KfJn639j5Xk9JPJ3m32fqi/yJEs+m7cX3S/08KPF5
2v7U72fm/tmN96L/8PsNxIfxvoH4RH7PAfl9kXyT8tnIzmWant93QM7vO8Dp
EW/V+Ed+7wE5v/cA83sPMPY+9drrUTwT9hK/iL22fJMy9pIee5FjL4y9pMde
5NgLE29nziP19yqQnzL3zbvGROsnv7WctwTvm/MW/b3SisOj9J6R976xanRe
gPzJh16K6oP3upTHe13KWyH3sXr/zO9TUJ+8J6E9iktcj8qb9Inuf/X+Ncn8
fgXy1VKf2p5zI56j7XXx4+i+WeMN+H0L5Py+APn5vQvkC4z93A9jP/5hP+3D
720gn9hb7Of+GfuRYz/5sR95Ubkv1/tr7EeO/eTHfuTPy3223m8/K+2jctqv
zEJZf9N+dvscUs6O7Fun/B9hrS+JAzukXN/kp7xck9/2f53aQ37YHk+TQu63
90X354nOeqiw3k8XWxXFx6iceC3kM5pE8TU63hKvxf59w+woPkfHQ+K12K+/
G93/F3bGu9j9/YkXo/tyHe+IZyM9jD39pkbxVTr/EO9G+gWGse9PG6P4LJ0P
iIcjPYz+6b9H8V06/i838XKkJ34O/XckRfFhmp54OtLD+Hs1I4ovU3/bmvqA
iUez139Jel7Ss6LEJyHnPPLVLRLvxXmtPf8nOfN1YeXZpr1h4vNg2tOez5J8
9ottZL+o9mA//n4+O4pPC780+9Xysl/1Pzb3I79ea/Vkh8kV9b2M+96F8xvn
PY2+T+E+ZoW8J9D7sPvlfYJyN3nPoOet/5T3D8rk53z8AZMf7m7yw8NMftic
f3gV23Z5q0HRCuEv5j7nieUF8R/lnPPb8ua+OXZfb5+Hc996MnY/beTs1yfL
/aPmPyL3b3p/v1nu6zR/rtzvqb9PyX2j8mGTH33bTH74uMkPP23yw+XlPlXL
e0TuX5VfT43uc5VT5f5Xy58p98ke9st9Rex+uoLRT3noh1cb/XBpox9Gv30f
Ervf9eS+VnmCqV+NV5D1ubf22xOznh9fTuP5uc88JA2rvPrZCVWnNfp+OSzr
2N16/0l+M5+Y9y67ld9bUefFLw6Fy2Hyw/XMfIG+42a+gNeb+QKuYeYLmPzo
yzL5YeYruLrJDzMeuP+/BvSz/oNZ78HtzXoPZn0Hs76DWc/BrOdg1m9u+dhL
+TDlw5QPUz7cypQPUz5M+TDrP5exj/UDctZLyFkfwayHYNY/MOsdmPUNjH7K
Qz+MfpjfO4PRD6Mfpv1h/KP85jnvSbze2k7tuyyoqbx+8fnG2+ZV1fGR83jm
h7tM/NM39vu/cIIdnxY+Z8evhdvs94FhXzt+LTxnvxcMg/dL7R7cNi/YZ8s9
1W+/HwydeLfQeU8YOvFvofO+MFxiv4/0p9jxfP5AO97P32W/n/RfsOP9/Kv2
e0p/lfEHeY4dD+j3NP6Q3okP9J33mL4TL+g77zP9FqY9B2bmtlz/QQ3/DsMN
1/586db+tf1t5j3l6lEF64HKftTdducGK8x7ROIBV/cq13lUj3R/iol/2yvr
A42PKFU96g9+krk/LzXghyG1R8f+/1P0N9KvkPJCZ/2O/uDqEpEb+7yKDVpH
65Fpxp6NS265fcLeSuGr8v5G4yeceBR/uLzHUTnvedqaeBKzHgjSRb/+Pk7z
e8Xefm9OieIbuE+/ZN7nT5D9is7/nC85+0k9D4DZb8Hsp3V+MvspuKrZP8Ps
l1z91B/6YfTD6IfRD6Mfpv20fcz6cuPc9xa06lgu5D7aq/b0+j4fpIWyrj1O
emXszWxYsd3ohif0PcKuzKRrRfOO6fsHfv+E+id+495mo7NL350WJpr+9enF
KF7D9K8L7H99c/8ftDD2oO8ts7/nvXA1E59Cfx9izQc5QYX+bwWnl6Zq/BHv
v+gf6LvLxN8curNcgwJ+zfRH4lmceKbwHdMfkfM9/Gi+P3N/5yVdv3VatXcr
6Xp+d9gmrv6I2P9PF3v7mv5JvAvxpzUWnSp1qXU5/3mRazxMKRPv0Kz2utXP
1EzV+JKS0fearO170wN97ls2L0V/T2boDd2mPf5gqv+JOQ/L+m+/kqOqlNPf
55v9/v/WR5bXqZfYJ+f2J7T/1DXvjcdH9iVr+UcaNOyy63JZN7/5PYiT2p/8
v67q+duXJ7S/IKd/rSm+cemzB2PvXVgPsR9bnf7Szu+6Zamc8YD4b+qL793p
L+b7zg3mmPFRf+/H9Ffuq6VfxX5vhvMZmPGjuGmPvLo/Pbb/uVTiX7zvixTc
p8TiR9jfdfnHC7vGNov93vW/7HjH0N4fltf49xktZHzmPnOpsY/xS/p5iu4P
33rigweq+SnhI6a8KHmzlJD4nMxeBfHNsXie5ksL1t8af6/nCfRX5pO7TX8q
M7RLxLT/U8/knV5SL8bh/om3vPdsjD9PWjOyZzeN3/HaXS24jyul8Tvl+/49
f38Xi1fg/Rnp6y6M7vM0/Wum/znrI/19HtpT9rO5Hu39vvQH3f84v98QDjLv
QYmnumSPT3pfm/HPe/L322WVK3qLL28flKL3r898I/ZyX7d3xqIRm5uV0fvG
Iiej+z3l++R+UO8b3ygd3S965K8q95MaP5Rb4c34bw+W1P7Fe0nKb9gvus9V
e6bLfa/eB+e+EN0H633gxSei+2K9D9wh98l6v9pX7htVX8fvongrvR/8Ve4P
1Z+lcj+tfGPN6H5Ty4uX+0e9335T7rf1fnW93J+qvd+2iO4vtT66Xovux/X+
uKXcz6r93eX+U+Xz5X5d+XJqdP+r951j5P5Ux88Ncj+v7XfjX3Ztfiozdv8d
J/fPyjfKfbX6207uq1V+07Dovlv9Wyn33Xo/e+Cx6L5c7Zsr9+V6X7x1dHTf
ru3RWu7b1f67W0b39dr+B/ZG98XaXqXkvlnrc86U6L5a22Ok3Hd73CfXkvty
Ha/4va5JRl/cuCj+T8dDzn+d8VLP54bLeKTjFfdtgwzzvTu/3+IPst9n+6wX
KG+S+T2ST8dVi8bPXvb62/19Gf92WT97f5L1c+gbHiDr69D8Pon3X4kXDjOM
fJPsp/z/M1xd9lv63ob4HZj4Hd4bJch6gPgeb7Osf3W94Jv4Hue9khsPrfu5
Nibeyn6vm67pibfi/KyynJ+pvaHsB9T/qmb/SP1sMPtH/Gf/4dSfxls75evv
95j1flDFlG/Hq6VjXxAYe4hvKmnqC/lWU18dgqz7Psw7HbRt2uujJzPL+ex3
aU9nvxR6ho0//p2Gjb86n7I/Zn2aLPsfN95K7THtpbzJ7GdIn2jWf/CL9vus
gPdZ5Od8k/px2lftg2lfJ95f9a00+73/B6rc9sE=
"], {{},
{RGBColor[
0.33397672886243995`, 0.12792855345845733`, 0.5864250111696041],
EdgeForm[None], GraphicsGroupBox[{PolygonBox[CompressedData["
1:eJxNnAe0VcXVx8+959x7zrFXMIqgYhQULLEjdnpXRAXFjhQVpVioKs0aTezl
M3YBu6KCHXuiRtEIKEYQBMVeYq/f//f2/y1c682affadPnt2nXmbH3vKQcOr
SZKcW0+SVPkyJb7XVWqSJUnHSpI0VeqgH/dU6qMf/6t0nHCdlZ5Wmd2zKLNE
+OOVd1HqpLSR0l1JfG+sdI/gV7PAP55E/T8p3Z3EN/ATSSTKP6m8h/rsqNSE
dpV3Nvy92lmoVBE8Xaml0kcqv1US+Z+VWms8lwu/hVIrfX+itLXStsKfKNyW
Snc4/9i/few23lPb893+2yp/rOc0R7gRSgcIt43SEPfdRvBw5X9Wmq8xfqA2
WiotEP6YSqzjOarXTd8TBf+o/Aev4/+Uf+1ym6rOcqXmSm30fR3rLPhCpULw
Rcr3Vzsr/dsy1bta+Z3CX6r8RqWlgv+u/Aal/wheWI1xUO5CpWuV1hb+UbVz
llJX/bZM+dtKa1ZijckvU5lRwnXQ72fq+xHBZyp10vdSr38u/HhoRvkE5cMN
n6z8J7dJmeeUP6t0TxZzWKsSc2ql73WUrtL3JsrfT+O3CZ4vbY8VvrP6HKfv
C5RuUtqsEuu0wmt1q/d5peC/MCfB9yWxBqxFN68Na9Rd6WhomrZU5i6VP1Zp
UCX2Zi+v8y/C/ZzF2jyv72bMIwk6pO6lgt/Rby8rHeXxU/c64U8TfKrSWH0P
UN5faQzzUX6G0gTBg6mnNFrwgcr7QFuVmOceXoMjNO8tTFuHKd/MNDdA+eam
44NVr6/SKMEDlR+hNF7wLlnsObQ3WfBEpWmChysfyjgEH6r8EKXTK0GzH7J+
SpNM75zf832mOb/f+Fz8LPgo1kjpyCT2+xfv/xL9Ps9lBinfW+McqfqzBQ9T
2lffJynfT/lplTir7NuWSpVqnCHO6toqs5bScuEeUn60Uvtq9Ped+/8gC7g3
Y8/i+6skeEwn85ap5lV3m8d09lyaem2Y417a03ZKJ3DelW+i/CnhfxY8zDzo
K7X9htvf2Gtyr+CHhTuOvdfYFivfQOlb4T/zOnxrWt7DdHVbJeh1Z/OqW7wG
f+WssX8e1zEeG+M9zmMe6t8HMd9K0MWuSdDR4YIPYb6srb+vgucoHVkJehyo
fDS8gjPl71807p//wLuP97z2MI8bqu8VlaC1XYRPVO/iaqzV7tXgs4MrQZuD
Pa/1VOaSapyphV5Xztr7laBfylwl/CToGd4keAp9VWMfjnZ5aP8kz3Fzj4Ux
tKsGH+e3dy2T2OcDVHd/1/8/jaGnzyZnYqLX/x/QpL/hu5O8zrcL168a53RR
Nfg+v+1SCRznkbMCL4TOOa/QdR/4s+AL/N22EmcR+rxCuMtd51uPETrsJVyX
avCBn80PJgt/jcY+Tfhh1aDfY13+DO8hZeBVpwreT/DNSt1U5xbl1wp/TbaK
f4z3fGdwxqvx/Yr5AGvSHfleDR7V3/WY4+6VwI02bd5qvvqgysxSaqN0ZyVk
J/vS3Xy1udICw0uFP15tt7AMhv/Ch+Gh8PDLlPSXXKmxnw3dVEOO3+79XVYJ
WoFOkK98f2T5TBlkNLR2m8vMd/vIuz2rIY8v0ndL57sJv4/GvbgSsgY5eHMl
5Afzu8Xt3Oo2kSV7uSz8fGkl5rFTEvWojwy9yfOpeK2WuZ33qqEPwTs3d3nk
1ftJlEfP+q4aNMEev1eJPmh/iOfOvH9wG5x9eOLMSugprMF0r8lM7wVrM8N4
1hAc+4R+8xbnkPOaxJm503vHmrF2m3rf2L8WSmtWow7laW+GxzPUcGP7M93O
B5XgR8D0t7yyaq+Wuzx8nXKN8/jA5eErKyqr6q1w+dZZ6AeLvfZLK6tk/JJK
yIstvHaNuPe8hjeq3kHVkKfoKrubntnbwW5nai1JvqxH+wcXkoW59k51divF
G/XbNsJ3FPyI4H6U1+8v1oKvHSD8bMEHCt9DcE/BfQTvJ/ghwT0F7y/4YcG9
BXcV3ENwL8EdBM8R3Be6Efx8LfhpS8EfaDxba7y/azzPCP5N5+Nm/T5Kfe+j
Ms8KHi54DdV9WvBJguuCbxI8Mg9Z+4zgkwWXwt8oeEQesmljtb+PvjcUvpXg
T9X+tuprqX7/Ufi3VKa38L0EH6Qyzyk/Rb+tLfgGwafmIX9vFXxaHvK7onFu
oHa+EVwT3FTw96yP8u1V7nCNfx/BGwu+Veu/t+A/1YJfbaO8o+o8CD8XvoPg
qwRP0Bj203d/1d1SZaYLni58C8E3C95b8BiV2UlwP5VpKfwBqttd+PHC7yv8
ocJvJfxMwTOhPcEzBM+APyjfUN9Xow+o/DJ9b6R1KNXGxoJ/0vg/1vyqgpci
A1Xmc8FtVeZD4X9X3cXwLOH/JbiH1ueFWtAHtNFeZZvq+xq1v1y4XwS/g5xU
fpd+m4W+QZ+14N+tlN+p7weYI+MvQp9/XPjBqv+94OsFf8YY1M5BKtNb3wer
336C+wg+RPC5yg/LwzY4uoz9Y+8SwW1Ut73W5BDBj0H36G1l0Ap0coTguYJT
wYcKflTw1yozsAw6g8YOK2NMjOeoMmgROuR8HJ/HGYH2j86D/jlDA/I4R8s1
pyc0hh80hnOE7y/8rtU4E4fncS6gu4F50B7n47g8zgjn7Ng8zhrzPjKPuQ/Q
GJ7U969JrMFReawDZ/GIPM4j5++YPM5gW5V/Q2NopX77C35Cv/0EbQj+UPh1
VWaWcFPykJf3C55EX4IfEDw5D/2AtRmUx/oUqtsWmtS8bhP+dOH3V5mnBA/L
kwbBQD9D8uiLNT4xj3Vm7EPzGP8tgkfnoRvfK/jsPPhXpvYXqP3V0C+1hgfq
t0MroSdjqCPX7hJuQh52HHt7Qh77e7fgiXnYnHcIHpeHHTVD8Jg8ZP90wWfm
YePdJ/gc1lzw4WXMgfHvK/gs1lD4mcKNzcMGvF3wGXnYws0tZ+HxZ6r8XzTm
vlqTnZXvr3Fvp6aOUT5K3+egnwkeLnii4KMEnyx4guD1lP+eh03cV/gB+j45
Ddxvxh8n/Bjhp+KPUOqdhg60h9aoXRb0ht+gexrn61iVH63yk/SdKf9M7byP
HSH8EH2PFT5X/hVnR/hc+HoRNvpG9fgGpt6nrtukHvwOXrchvpMi5Pmf6sFH
4CHNBK9ehH69fj14JXwSewUdEf2QelXXpexqLn+i8r+rzhUa26GCjxI8Ml2l
X6Jzvmk9cNtK6FXIcOzTbv5+U/AbSehlryehc2A3V41Dzr+XhD/gQusp6AUn
WRajgyyz3J9h2d/S8nm5yyy1zN3C+gNtNrcu8IHpgT1hb/BXYBvuUAk7BTsG
GFsGW6WN8diRO1ZCx0Zv3qWyyq8AjI6Kf2Zn10UvRr6jG2N/0Q4+k8+zsAlZ
H+ycna0DYHPu6PXfQ+u6vuh4T3R7rfOR+h6hde4iuJPgIwU/iJyFXrVwVwh3
eT1sl6uUX1kP2+Ua8nro75cpv7Qeuu2pyk9ROktwX+UH1+PMdlW+C7xJ+LHo
DPXQz/i9dxFl+ijvVYQeNpJxKZ2t8qcrP01psuAzlZ+hNEXwFmrvdsHd0OGV
r6fvdoJ3EbyW4O3Zf2SvvvcRvBs8T997CN5V8DqCd8DOQlbre1/Bf1N+CXNW
+/3qMSbG01nwTvBc4Udo/Lfpu6vKd1S+I3wcX53KdtD3EYKHp6FjoV8NE26o
0rg05Oe0PGQovO0/9eBv6FkPWJ5W1f6bnKssdKVF9dCXluj3drXwb3VS2/sL
P0BtrqHy7wo/W/jDhD9a+FHCdxXcRfDRghfp97eVHlKZD5iT4AeRC4KPUZnR
KvN9Lfqg/Z8EL8vDLvy5FnIdmd7HfAZf2Q+10KXQoyjbvhblV6CX1cJO/bUW
38CVeugZ6BgnCT5RabzaWokMqYUNkdTjG/i3Wugf6B6f21cEH7g5C56NzYlf
Ch8PvqnDsvDvIL8OysLHhEyZWg37mXPOvp5SDVvtoizsWHTIs41r0LvTWI9B
trmx0dHZsVPxT+GDaG0brsFGqkZZ5MGQLPxc6K5/V/43+33OV36efSZTsvBP
IV8uy8I3gUyZkIW/DDv5hizsdmQZutoB9kWfkoU/C5l7cRY+FGTotCz8IOir
DX7aathVnLdx1bARod2xXotBxjHm67KwpZGV/TL716rhnxjguVOuueVv0yx8
5WvB85U2rYbdVLFchAd+mMZvnDXWm3OAbQxfXK0a/GrdLHyhOTIIX1YaMG1U
3NfiNPgQ9tkm7o++mvmb9rdJAm6dhE/m0GrYPEdm4R9Etzk8C78k+gw0d2o1
/IuTnLNW+F4ON53Ad0Z4/uj0Z1bD9wPfGWk64MyPqYbfCF9N/2rIDGzxYaaT
zdCzBRdKV2fhn0KXuDILX0kHz4M5tbZdia2IzXhwGj71DTxHeBvzXTMJv3kz
ZAr2LTYlMsX5MMsUfJT4DvsrDcXO5ow4H4yu6zLUX+4211Jah3VEN08iLrK5
v1Hvmio1UVo/ibFtobRhEv487FOxk2Qjl6u7LL9nngf1DkoDRt1az23QxyVZ
+GWRVWt4fpskDep88ie3u7pxGyudnoXfGb3uI+VvWUYy/7FKY5R6ep6sUy+v
B9+fquwn8AvBPfw763eu+QwyFLkywOu3QvjXLWuvz8LXhv7JmT7Xesme1sew
R7q63mGW4+O91l9m4U/Ff7ttEnKYff1O+G+Zj/fmDObnvTrT3//T718rnSB4
pfIF1i3ww42ynvSd50j7bZTauw/oYpzXZS+vC/P+Iot1QT7u7TXiN/QdfBn4
NH5Jg4bvELyzyu+Uhc93ehqybox5CXwG2p+Zhszh++M0dLqzzXfGmqcONs+F
f3KuOF+tfRY5m5zjf6Shq/KN7TSqGv4tzvc5PuMz0tBZxvocjjH/y9KQG/hJ
8XVjryBnL/Y3/ll4agfzVXx8+FHxFeBL3d8xD/IDjO9kv/hNSfg1aRtf9Q1p
6PUj3B/94r/e0+03xF7cDvASt3NzEvxlhPnH7WnIc9biszT038mWP1PMh5kH
47/Y/Gayec7dWcR10B8S8094yBdp6AJTzZOmmS99mYY9Mc08b6r53udp2CtT
vN7oCMg3/ML4hzs5RxfAj/dJGvrjOeaJ8Eb46E1p1KWNIeaz8NhP07B7+L43
DZ2Fva2moUcQt7snDT2Ffm9Mw46h3TSNfumfOA9lOzqnLvGDA9OQFfBT1r+9
95cYVlfv6UjPeQuvKWuP/22E13RzrxG/468bbHmPzj/K42ppmh1sur0+DbsN
WUf/yCz0xq2y8Gn96nMypLoqxkCOfXGqaRqan+0129VnA5mJf2+y6Zt6H6Uh
c5t5TamHD5b942xhp4zzfjf6hcmRy+zT7j476DuMt4XP5VCfTXxk22The2np
+V5k+mcNiUcTMyGGQtxkkfeGfSGWsafpvJaGrrfEe0PsgbhDO9PwocZ9Y/ri
THRy+z3TiMuiZ3Zw35w7+u/iMp0No/u9lMU3MD5m7FTOKPHilaaXn/T7j0or
quFnxmbF14yuyVgZ57vmHZxjeEQ798uc2nnM7T1HYM45beGvJpZI7I544kLT
9ALPn3VgzTgzjI8YB33zGzEo5ORWlqPIwh2TsE2qWcBbKP1TaY7SI0ovCv+C
0m7YCFncJ3hZ6QWlh5VmK72SBJ77BcQssFOxjxG8yBti/a0sV5Gv21iuIl/x
MwK3tuwZbFn0b7fHXYUX3Q9jel7pIff9WhKxxLlK85w/nYRNTv5MEv5Kyrzq
b3yBs/z7/f7eIQt4rmUg/Q/1OrFe6BjPuh4+VeLgO2YRy3wvjZgl9PlfrwVj
39r1NrJ8RMdA78F3s7rnz1qgc6zmcoW/N0tCN0InQo9RlQa9Bl8CcZXlbg/d
BR1tZmXVPQv2bz3XY31Xd7lNXXYt/151uxu47ZrHm3sc0AN6FzRG/GWlaaat
22pu2tncfe7gcfONPdzC39TZ0OtIqruPbT2+Zq6zrseFLtB436Sl58EYE8sZ
6Aj/Nfv5rtIS0wH739M2YxPL02m22/BHn6d0fhL+rMuT8JNfqTRN6dwkaAsf
Nj5taOv2JHzjVyhNdTn87Jcbd5tz2pjtstS/xv1ckEScizsXxAqvNY67GV1s
V3FPgPsF+E3wmaBjcWcBXw36Jb/jh7nVtmajzkqO3wab7xLXh16WeR1bCNc8
Cz0K39Ny73tH24v0gdzBlwSvXpzEerKOvdKYL/PEJ1R1XwuTOIfwhgVJnH++
ifvDkzir85M4n/zGPYHG+0fwAs4eZ+htpX8pvZSEj4x947y+kwRf4fws8u98
42+jTXxuc7O4WwBv5x7NlCT4NvsH7+Dsoneil6OHogtjc6APE6sn9oo/a5x/
57eKCP/HLO7S/JCFLty436e7XfZzjNsm7k1MuX0l9hMc7REX5i7CBO/xOPeP
7wnehp7AHQTWnn3+PQs9m7scFeW/p3G3hhgmvkT2Ej76ntfnzyqzZRY+9nle
O2i/veUntu5haezTP70P871uL3jP5nvPFvob+YQc+dB7T3uLvfaL/rBX5G+Z
NljvKV6jK0wn03wO+F6u8byfhZy8wHTPmYC/wnPnJsFzn/H3y957+jskjbE/
YnpkLJzxWaadZ0wf/3UdzjRnm9jWHM+b+T3sObMG8DT4IvwEnovsYT/gO/Bl
+BC8t5XLbWIc5eBzbV1usyR4HLyN+zzwRfgTPtol5o/4dG8x/2rhstuZzsab
JrizwJ2HhrOVBM/jzH4s/KIs6BNZy7o/moSsYx7PJSGHkcHsD+ft314PYs34
qDkrrNEbppnH/TtrPNtrw7o85f1+NVklLxvl5zz/xn0H7jU00vWFf5gDMHu7
p9eq0f5r4/UaZz0dXbOd15Jy2MHYq9iq+CLA42fAHkXuc95+zcJm5m4P9iE2
JPbiZNsW6NNn2V5Bh8b2pc1GG5qceCV2dg+3gZ2KvYmtOtA4vn/LVtmy2LuM
q1H/AG70Z/R329zrgSfDmxv9IPTDnSB88NjsJxlHP/Bq/CPw9pONYyz/ycLu
xz7HTsc23tdjYq4NNnIWdySQIfBz/DqcC3xh8EBoAx0E3YX9RM5c672BX3Hm
OBtj/H2e15ezytmFl8KjH0uC/8H7ONdjvbfUgfed6zqrSzG5sR72Fjwf2oK/
I2c4e8jN95PgW8iiy8zLwGFjDbJ+j86xvum+UY4iV5G3nFvo/XLjkNHI1Dmm
X/Qs6B55M9046nS1Po+sR/53s817mXh70zJsmDsFj8/D54lPFN8oMU1s03+m
YVNiy+BPwJ7BlzAvDduFPeAOImuMT+mNNHSSXbPwURJTfigNv2ej7wFfwVDb
btja2G+z0/CT4sOYlYZfr9GXgH8Dm+3+NPyA2E7YKcNsF2DT45/FP0C/3EFs
Yr8m/k3u0kAv6xje0L4T/J/YT+tnoaPi+6Q8/s9mWcyL8sgB7gTC18BvqrQi
jd/55v7o/ZZB6/j3Zq77q/vqYvpsYjlNX5u6zNNpxCrwz2KH4m+BPyxIwwaA
JxNv7GMZ81Ya8gCaZz97W2/r7jLgFqUh8+D77MnB3hf2G/scmft8GvwCXvF6
GvuHrosNPtH4N9PQy5EP+AvwG+AfejYNXsY46benx8a+9DCNwedGeL/gT6NM
A/Cnkd5fbN+TPXfOwWjTQHe3g776XBr+Yvp9Jw27Bf7c2f1S5t00dF9kYi+v
yWVet15en6n+jbNM/7M8hjt8VjmnD2Sxl9wBQudA9+BOb5qF3t8o24DR7fEj
cV+TeYNLbSvWDFMe2qkZhr7Ye/Yd+l1oGsZXj08Bf8Ih3j/2jrm+bTsNPveW
95395M53S48tc7/oLdjX0OwTWejBxPqJEeJvwtcErybeQZz9G+ta+DMvET94
TXysyEKnwl/CWUC+fGEZQ9wR/xS+KWKN+BbxIRIj4J7FcMugzyyHiFnib4J2
oJdPLP/wZ9IPPk1o/E3TGLS5Mg3/zRzvC/Pd0mNiPNTZzDo8eYts1R62cHny
zSwb8P1sZf2Q/eWOF/cuaG8rzxM9EX8LuiJ9be3yW7lfYO5stbLsQXdd4LO5
js8+Y9vaMO3DF5anIXs4i/9NQ7/c1DSwwjT7jul5+yzWkLWEd25u/tnM/Ib2
NrZdje2PcUp8Ej8kcoSYGWcImqpn4TtZy+NgDJzj/6Rh98JTHzBfbYg3p8GT
Oa/3N57ZLGJa3OsgPkecjrsA3D3G546/nXSuZfZjWdyB4/sxl+G+CvWI83GH
B3sMuwz5j85P7Iw7KsTnoFV+n208sfrHs6hPXegZe+8S/36x6zIm/O9tXZ7Y
JN/oI9xdxk7k3uwgj//ELO6Ec1fnBOO5O0TON3Nl7Od7/JQd6vLceSa2yN0h
3iWMySKWhO0IHhsGHL9xXwjcEJc/Jov75MC0yTiIG57h8twpIPY4wXXRc/Yx
vU30N/KWeBpxtX62iRkTdjFtH+X2uXvM2w/q7et2uJdF7K+96Rwcv0HXwHu7
DPET4ijcadnL5YHJ+eascDce+uAOBe85zs4iFkOfk7KImXK/l3cU3PEdZ5i7
Vcx3vOeIztEwZ7fDPWF0j0keP3NsaCOL2Ch+C8rgY6TPs1x+P48HWuX3ycZP
dBnuHs8ynja4I86d5v2SWLOjPRdy9okY7otp8D70avgdPnliBeg+xLDRf+Cn
6EnoSOhKUwyjpxBLQMd5IY1YJnXPtv5EXcriW8cXTprkvvA/o0vig74vDT6L
jsR5vcpnlvaIeSCr0ZWIA42xfH7OshJ9ijjQOMvehyx/0bnuc5t984gB4Osm
VoDfH10UfY24zljL5NmWy6zBC54LchvdZWeP/UWPH/0F/eBQ64wPp6E3olOg
c6BXIM+JLaHvsJb47tEF8E218R5x7523QNzH4R0BcUbu6YEbnUXclndRI7OI
3RODpAy+DPLTXX6CaW5yEud4mHkL7yegAe6BnJzF+5Dexh+fxT0BfucbPne8
4R4++2eYhkd7nAd6nIyJuz/c3WQu6KX3ZfEOCZsEPse9BOQyfPdq817W6Rqv
1Vi3xd0h2jvVcxnp9oH7eszwTHxm3EmA54FjPvBU5jvcvIv8FMO7l3G/k7N8
uM8PNlqnMu7dQv/4p4ta2KDwU/gqMc6bsuDz8EZ4MTwZvxu/35LFvYVbXB6+
fW8Wb7GY/7muS3yXuxU3mOfwXmBmFvcE+J0+DvL63+U1v819sW74Cng7gb8A
HL/hB3wti/d++AKwIXmbg23LHTDitfiXeGOFHwY/Fe/JlnqdiV9zxwuf/HzD
yA58CrSHr4B3V/hx8OEg8z50P8SliU9jm2e1wHNPZrHxrO37rku/lMHGZnwf
ewz42VgD1oL7sdM9R+5twkPxO+BzeCqLuyKUgScC8zv3GrjfwL1ZcNe5DH45
YuXcm2Ut7/Z67uA9wf/EXj3+h/0Cj94LrSJ3G/f5Ca//hS5/gcfIWBvuqbov
+C1v9xgTcg3c9R4Ddy6u9LyQOf8wDVzjueNbIYbKWAd5vuD5/cks6lOX8w8M
f0De0A7yrpv7ZR34DVrBp/Skx8o3+i/3ftCBobfHTM8vmTbW9H4tM8ybqte9
v7xngQ6QQdyHxGeBHME/hZ8KPoPNx95jY4J723hslpfc5sumI9qhjTfcznK3
D53wzpU4E36vFwzjl3jN34+ZJl/xmtMufU1Jwhfzlmkbww6aRs+Hl73pvvh9
ocvwO/cZ8LtyThaY/mlvkemTcb5p2n/Dc//KY3jHY6befNftaTxjw59MX9yv
IKfvise7zOuD3+VVzws/MOvO/ZCGN3BZ+II4W9xF43x9aTxjoOxnLg9/+dzj
5BxztlkPyn7pdkj4l/ApMeaVnnsv43t7fT7yOL9w3d7uC56C3sXZft1wqjlW
a+HP40xztqEL+AfzwjfEvrF/jbjXPN+J3sdLzU/muc1Fbof1b6QDeNJKj4Ex
19wnvrkVpj1o9VOvybceG9/4IsB96rXibHJuG+/ScBbg02cZz94xJ+p3cV/1
WtRteA9di7FhR/7uNqH/X90vevlv3i98idRnnJ8Ypjx1aZPfwdMfvkvqwSv7
eN+BP/DYU8/5U/fVxfyeOvgtf/TYoLdBZdyzR74cX8bdevhV+zLu0CM/9yzj
3Qu6/KaCl9TDNzTP82Kd9yrjLju6xt5l+M66WFZyxjhf/aRTrVmLOwPzjYd+
2pXxXoK7Sc8XQtfDXt+jjHdB6OG8y/vF54j35t/5vPQt4849e/Q3wQflES/8
Se28UI84CXI6r4WflrzweL42Hvjvqrt6LeKOPcu4T4/uRN3Sa9WnjDv32DXg
VjO+WxlvBrBZWFvw+EYLx7JP8Jr/ZFpdzfGj07y/33gNKZ9br5hvPHVp43uf
tdK/45elPdqZkgRP/sX8gm/6n2oe9ZNxC90O/TKG0uOkzs/mM41vIFnnF7n3
juMLfaOMNwnoMPhHr66Fzwy7AfuB+6LkDxrGH4C/CB8APmf0vEa5CowM3dJl
1rVOSF30QmxYbF3WE9qvmf7R73jzP9C6KPY2PHuYy6O7nmc8Oio2C/ZYw312
jxP9GT8H/g7GiBx52nwGmYksvNzj5I08OsDtxqfWx5C76A/3ux3GP9ftNLWO
QRnk8qUeM7TE73PdF3oyegA6wEauT4zyKuM72c/A+NE557gt5p57PaDnY8p4
o4JOeFwZ72TQ9y4V3KwWPv+tBF9ZC9v2MnzbtYgVdSnjrRp2/dbKL62Fv4i3
F0U97qbM5R1YLXy026v8ynqs3y6Cv67Hfbv3i7iXj4/rFcGz6+Hf6VzGmzf2
onsZb9XQvQ8u4z0Musn/VP65evgT9xM8rRaxsVNVZrdayGJogHMCP/xWZf5Z
D7/eJ3m8IeENyCSV71IL3+SzKnN/PfxBvcp4V4NOdGAZb2/QDXnz1NfvnobC
N+rhdxwu+M957P0PPvucNXwyxMLxK/TR7zeV4XPk/z9gI2Bfc+/+7iL4czuV
ObeMuOMueYyPse1bi7d/2D7c67+jCHnLO4AZRcjc3VV+ahnxxbVV/vYiYloD
a8F/4b3sw5Zl7MV3+n1mEX7O3VR3Shn3RPYUfF4ZPrFdBU8uwzfHG7tty4gN
7CT82WX4UnfI470fvrcdBU8swy/GO8g2Zfjw/iL8WWX4JXeGzxchX7YTflwZ
91vWZt61sJ93Fv6cMnx5bfN4X4GPsE0e7wbxcW6fx1tBfLor1d7EIuxt3kzc
VUQ8kPcQ04uIp/JWsnUZd8GmKd8mj7gm/P7XInj+67x9qIdPlPVolceavCrc
PPty/638tyLud/OmcJ8y+BBtfON2OqrelWXEAE5WPqcInvCSyv9YxHz/Jfj7
InzZ0N0PRdAeb0Y3KsPPCl3/qwjaZrxnlDHmA/I4k5xH5rS154UsurEIebRH
HvOkPG8ubysi5geNtM6DTi7nLBdxz/mjeryjgy+dj3yvR7x+2zzeg+HvRA7f
Uvj+HvK9CNrgbcqtRcShv6jHOz18vPcIv10Z9xXvYW3L8Md2VZvXluGbh688
WcRcugl/XRn+Xd56PlREXO7fyh8uwu/Ke9DZRcQXuqv8/5UxzuZq56ki7g9c
Jdxeefj1981DxiPf/6H8ojJ8/Zz7l+txvh7hPUoZ/m32rX0ee8cb0AeLiHH2
EO76MuI/TYSfVUQssYvw17juJsI/UUSssWce/dFXL8E3lBGH4C3sA0XEFTvl
MVbGyXvW+4uIpfLG9PEi7iMgn+Aj2BCdVf7qMu4FQI/EGKDJ/fPg3fDtDnns
K3sKLV9QBj3zfvexIuKdfxHuk3r46O9T3rEWsZcNOPf1iHm8obKP1SN+cLh+
f7oI+3GIynSqhV37Fby8DF/7vfXom37fE9ykjNjgx/Xoj754p3VPEfH8DQTf
V0Q8nzdP9xYRU2c/z/eetsyjP/qC3zxTBM+h7Stq0f6Ggp8rIuYITe2dB12x
J+wr+/Kg8r963TrUgnfDt+E9nEnO43556HOcHd7yPlrE/RHWm/rUhX9faB4O
ne6TB63yHvqRIuLIz9ZDPiGbfq7H20t0m3d5q1XG/0TBp4S/Cf8Y9jn+Ze5u
jbIfijg+djf/3wHfVcO7nyz86ujZvPvAV0POOxD8wPh3aQcfL7/hL+aOEPkA
l0Ffx9/d2OfAbJVPuL/LHGmbf3eP5WCPs4fHgx+gaxZ3y7D3+T8YvbPQ2xve
M2X21aDvl/F/RPidcmvYfwKMzkiMoI/nRX6gYfQSYNrr7L7wxZHTN/YFY2FM
2A6019Ptv2MYXZQy3TxmfGr4QLljhj7KvFhv8n6eI/TEewDsLfgC9y+hDXRR
YPRPYofopHOTVb89ZRsNvQa5xh0NYgP4K7BPiAGAQxfgLBNnOSALPQAdYD/D
lCHnN+p1sv5AefTfHT2G3qK7G8uIgXEPmBg9sS3yXQ0P9Nphp6Pb8Y6scQ2A
8a+SH2YYn+shhlnnzt7fNUTbo8q4O8pYGBM2XVP3RQyeWAbzJa6BTwX9GH2V
3xhT4/8gAw+PIt/NMHwfGBu8ufpZXo9YHXo9cpWzgz5yunUS9KOR1pGIr15h
HviZztzHRdyJRr6dZl2Id5kvF6E/YJe8VIRt8ihvImsRK54j+NUi4oK/KH+l
HjG/55Vvhy0j+IF66EaMAT1lzTJ0lTa14JvwzAZ6N82j/84rQgfm/Xdaxhvw
+fV4Ew7Mm/68jPvXi2vx7pF4xdv1kJ3ITXSQ0dbN0M23tX7+eD3e5BPj5L7M
h0XEOT5X3rYWMeG59fgGRqf4qgi9Alv5kyLs5afqsXas28JavKUkdvGF8qfr
Ec/9f6fuXG8=
"]], PolygonBox[CompressedData["
1:eJwtmHn4jlUax5/3fd5n02oLbRKVFBKSfV9+KvKzlpA1Zd+1iui6mmm02JvL
aCUaEW3TojGRzKSZlCyNbVRITRLZM59v3/njvt77e+77nPOcc+71rdRvRPHw
fBAEPXNBUOD34TQIWsbgMAheE4EbgOcgmwt9mwRBefBxJvVnzgjwEXAzJp8H
PicLgh1RELyFfBnzzwevRx4hPxeain4A9Ybvhs7nrD8D/Uvg96P/CLIz2h95
V8bmIevKWG2mVQRPRn+WvgfdFdAEZBdAM9BviXwsfBloOrgZ+Gn070H/fnQ/
hB5EdiE0H3kR8oPINyBPwAl4DngieCq6H0P12L8nNJCzNecbpjD3V+Q90O+C
/i5wKfDP8H3ReQh8EbQAeXvGHuf8bcHfMncT681i/dHoPwz/EbQfvB18Hvpf
oz8U3ePgm8Ex6/UFx9AwcEfw71mvCNyNuVugyfCn0e+KvDPz7wSH0CDwLeg/
yfrdwMPRXQ3dAR9BQ5DfinwG8qHMfwDZGihk/YvAJ1mrBDo90c1BfeE7oL8c
/frIG3KeRtC9yEpA45G3Zs4z3NVk6Ab4ytDtyA6j3xh5NeZfobOwx2vM/ZCx
Q6xXmbFl8MsZexQ+Dw0A34z+HviyzP+FtfqBJ4LLQbORt2LsdeY3jG2b86BJ
sifwbM6yXPeL7sXgU+gOYH4vcAqNZn4x+E30G8We+wx0Ar4J39cO/Y7oDEb3
KGNt4E8gz8AdMu89tmDb6wkOcrbBBHxz5rsdUfBet2S2Te2pu+qYeW/d2dng
TrIR5PeDzwLfCm4Dvrfgt78J3DxvGzgHXAzuwvwHwbW46/GcYRFn7QXVBI8D
Lwztw7qrO9APc76zq+C/4zzV4K+BDsBfyViJvMeqwO9nrCT6V4PvYv4l0Avw
RznmMPjLoMXgDJ274S+FXgKfRn6Kuc0z214xY0P5lq6MbQEr0AxBtyK0qOBv
ki22z+yrsskf0K2a+duqM1ZAXpTZ9gYXbOstMvuCbF6+dmfm2COfuxx8V2bb
WVrwtw7MHGv0zfL9PuCzc44BFRSLMp/ljwXHjtsyv7ViSEn5GvigbBNcGtwj
8108Di4F7g4+BH6s4LMNyBy7dEbdXb/Mvqk7vFi+pPcHP1ewr7YDN8nbZxUb
W2t+zjFSsaYluFPOMUe+2AbcKG+flK+0BTfO22fOBXfOHNseLvht+meOVXqj
88FddR+sN1UxG9wlc6yaUnDsbaXvzTkGj0n8Brr7pujsRV4Z+VUF28jAxGfS
WXQHvRPbsGxXNtovsc/IV3SGR7GHItboi22+BU0Dz5P/wb8J/U6+Jx9lrwxa
oG/TnSPbBv0BfBN4b+CYOl2+ljgWak4j+R+0EVwMDYL/RXdY8BtOZb+24D7I
3lC+Ac9R/IB/HRqf2Ifluy1Yb1TiN9bb6o7HKR5BTxXsk/fAH2N+UcExYHRi
G5Ft6E1HJrYh2Y7ebAr7tY7tqyuh2eDx4Efg10EzwSPBk+DXQk0VL6B/h76D
pvh3Nc5cnfXKsl9jxZfEuaULdIi5dXSHfE5tdAYkfmO9rWxqN/JLkVcCl1PO
AVcEvxJ4rCn8ScY65r3HteAf5ZN5v3kNcAWovPIHY30S25xsTTa1gO9/Ev2Z
fMu/oGvk25G/VXPeR94U+Yvs91Lgt2mAzr6c30i54sbMvq+c8TO4Xubc0RB8
A3zdzGerozdFXjNzrNqRc+5snDkXKYfqbRplfku9Uf/EMVexVjau2qV+5rmq
YRTrG2a2dcX8WZH31F5l9aaK/4ltUTn4L5ynMXOe5ywvQCvAVzDnZfhF0Lvg
JrFlOnMJxcPI+VU5qQl8GcYKrLVd9gsuDQ5l7+DesWsy1WKj9MbIKzB2Atkx
qEXsnKdcdzvUJ7aNybZGQ53Rv4Cxo+gegcrBF5BPy3ksTr2m1lJN1wC+FGN5
5m5Wjotto7LNKVBJ5O8wthe+Pucp1veCD6N7CCoDH6A/JeexVrFrNtVqd0AH
4D/Q98N/g7wl8xPwPvj/QCn8Qe53bs5jT8W2KdnSLCif+kw6i2qCC5GnjD2W
853URTYRvDh0jAmRH2C9Pf9f/5i+hbFVfOYu2Sf6f2XsXGTvBH6LXxnbkfeb
1OLtf5KNyb60f+yaQrXEbnTORK6JVQtrTlnm52LLIvSPR64RVRtuYWwr+CN0
div+KJ7Cb2bsdeUDxgbHrllVq96nM8SOmYqVY6E2sWOWYlVv6N7YNatq1WnQ
94nvVGfVmdvFjrGKrXdCY2LXoKo9J0PDY8ccxZqHZEOxa0bVisNEsWtE1YYP
ao3YMVSxcwz0a2Ib0NurBk64r62xY0Mj5NfD10Lnc9kiVBt8PfgL+K7KAeAN
qWuvr5UDwJ+k5vdoffh/Qt+GrtHnIv8KfDB0zngfvCd1bXFM8TNyT6FeQjb6
LvLPwOcg36d4C94K/m/omD8OvA38Y+gYXJvvfy/2Wnrzw3oL8BlwDvyTdKHT
+jbFuNQxVbFUNqS9Xo1tK9qzPGftlbmWn4vOqtg1v2r94+h8B39tZF4+sQV+
n9YIbROrY/co6k2055rYNbNqZX1Ta/S/B5+E3wldh3xj6rN2Uo4Br03ta8qZ
I1SLgX8InWOeBm8Cfxe6Zt6os6Y+m2L+J+oFwIP4/pjv/wKc4zzTlZ/BH6s2
R16LtQvgJaq1U+tuZo3qfN+n8lHwKfkwcz+Lnds19g90b+COvlS8YY9xyNcx
FiCvys86dI+kXjuUvmJH6rcoQv9zxZvMttYdvE17qZ4K/Y3b2f+szL6lnnQm
8s3M/z50D6lYvCl2r6OYXDJzz6peVT3ZTmRlwcvYprTyH/r5zGdXw9xJ+TVz
r9s5ce/UK7Ku1rsb/CX7HQjdgyq2HoscCxRj18i+Usci7XEqcs+jXucr5Vz4
UarndCXIuifuidUL18k79gXssSvvGKjYfjpyLlGMbwM/gvlrCu6xFJtPRM4t
itEPgbdFjkWyOcXeo5Fjv2Kw5g7P3KtpjT+jXy927G8AHU39Rnob9fjz1bsk
rkVUgz2HvLlqJnSrQM+CmyW/ffJvY7XZawJjL4euyV6QPrQz557/ORRbJ67l
Pgvd67RNnUvU86jXaZM696nnWQXfInEsXw99oP8zEvNboNXgHaxZquCeXnu3
Sx1L9Q1Xojsyc6+/UfU9/Ed84xN5z7kvsU/Ll9WjrWfusthn0zc/kLhHU2/2
Ww+ZuidWL1wPnR6JaxrVMqp57k/cg6j3UA/4d+W32LrygVfBN8a+a/XcwxP3
qOpN1cOM5/vqM7YhcE6bAG6gejHw2NPKb7F9bwl4LPIbE/tWBdUriXsm9Uo6
46TEPYJ6A9WAY9Cvl1i3hP4fStzjqbdTD9MFvCt2bdQWebPUOVf5RzXl7Mg6
kqnHVCx/G/k3oWO6Ysva2L6kGPNp6hyg2C8dxfr+qXObYv5I+H6pa5Fn9Wbw
ldijGUs0hZakfkO9ncZUCxSlzn2qCRQrW6F/T+iYqVjQJ3VuU0x4JbXPyddU
Q4/Q3NS5cYF8FL4yspuQtYeWgi+PzMtHh+n9UufO+VBz1eOs9xX8bcq3srXU
uf1Pio+qV1PHLsWsFpFrCNUO8mnVgicjxwLVhMfBdRPHvotyjuXdU9d6iumK
Nd1S14qKOao1bktdO6jmUK7rkTp3K+fNjZwzlCv0H9xLyC6LfJdNAueGIalr
L+WIhfAVI8saQ0/EPrPOqpr/Dd0/8sWBa+D3wNVU38CvhCZjTzXVM4e+k8WK
/6xxXeAcshJcJXLtvBB6B3x15LkroLf0PpFtWXu8Da4aWab/lJTb+6aubZTj
F+m+VL8F3uNv4BqJ724r8hfBdZDXCKzzvPJx4tpEOWlI7DfTW+k/suLYOU65
TTZUnr2Xx8696gEm6b+LxLWOapxRsW1ItqP//JbqrIltYTvUDFw78bfoTibE
tnHZtv6D7ABfPXFu1H8o6j1vz/xfi3rQ/wG5rKzJ
"]]}]}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{RGBColor[0.941176, 0.906538, 0.834043], EdgeForm[None],
GraphicsGroupBox[{PolygonBox[CompressedData["
1:eJxNmneUVdUVxu97d+69D0FFxYKJGpAiagYlChoTUVP+sCWYmKjRKAMOFiKW
2BJ1QE1mBIZBEFRgsBujSFGj2EDBQm8SDRHSTaI0KYNYgHw/9jcrrjV7nf3O
Pefcc85u3953OtUMOeeqcpIk56RJor+kvpQku0TfEd0v6qKHk9R/vdqLRF1F
Q0vRNqv/l2p7lWNcN/Wfx1z136DfF9MnulHUX9Rd1FMvqRbN5LfGni/6rsYf
ofYC0ffE31GKeZO9H+Y9IL5GtLf4AWp7aI0jRNP0+8UiSY4X/7L4Gr+HeT/2
+B+p/fmX9j5D7aelONdLmttHc19R30zx3xD/kvgXxB8r/sVytMeYb6O2IrpH
/CU+H/t9sipJ5ogm6Xeh57loTDnW6+U160S/YD1RQyla7vlz0WeiU0QnauwJ
olf1bIl+D3P/3urbSzRB/etF68pxd19pozvPk2RwGndwnO+BM/X2uT4SfVgO
2bRV3x6i8fq9UL/rRH1FzdyHeeS/0zrwscZtLIds9tS8dqL79Ht0Kc7AmHmi
t0Unsx89P1j0qMbsp3ZfUbP4HXr2hehU0XLRneYni5pEp4kO1NgDRA9p/FO6
y8Ft4l7ni+aJxmvMG6JMz9uq/Z1kdLjGP1mOvTdbpo+o/zD1/451xHcX/3Q5
zsa49qK1ojL6qPYZ859q7vxy7Ok063+z7wTdbqQ/se74XeOLOCdnfKCI83P2
d/S8ndoVjFPfSMue3225vyTuGT1Ft5e6v0Mp9n6o99/HuvKgxryr9ddnSbJI
fXtWNEZy32F9v9PrnC3+GP9mvXZec2IR98vdNvneWXOm2lR9u8T/RWO2af0/
InP3f6MUZ8m9ztQibG+a16Gfu5olqhKfqf3EMjpJ7UK1C0TjxP/bLXfYRrJ9
X+96Xn1bPLeP12Nd3jXausE+e6gdJdqYhG7u8nmbLafdPkr7qtX8M8qhM4tF
31d/Z7X/Kcf72Tf9q6y7O/2uLUnId53ao7TOkaLpGrtaY5/2uxu8J/bTZP47
1mXu/FTba89y2OxtagdbHit9j3cn0a4w39Y8+tDOetPBay73Gd+XnPfQfe1Z
FTaP7eMz3xf/Z1E/8VPNs/+x5XhG/0/z8BH4h6PTuO9VXnuZ1/+Txrwnaqv1
W9S3TfTNUviMtaIrSuE7+I1v/63WmZ9GPFjmtTh73zTuGPki273axPvmic/E
j/b5Vtq+0M+lPjs6s913stg2v8pnet/y2SpabR24CR+Zhr7fiM8TnSW+Fp+X
xr3frHa2qJ/4gfhg0ZXiL1M7Kw17fKcc+o5vebYUPh6f8KGomj3pXZ24w0r4
zqW+t/1EV+r3a2nEvw80prPOeHhVyGcD9q4xl+N70vD9l6p9SnSr+EFqp6Sh
I9zZDtsG9rLTNoPf3SQaov4aYmYauo0v5hmx8i71LUgjvl2tdg5xQPwNxCvR
meXYVyfvbaL6hlsvh4tfmEacXmG7vdsxs3054uw1on3FX6t2H/cTVwe4vyaJ
vn3sP+nbz+Oh/cuxRgf3M4+2g33OUI8Z5vYA8y+UYgzjZ5Rifd77qvgDvT6x
q9p+/RbbPb+5X+SMHe6j87VPIy4f6PWZyzsOKsf7m8yPdtvR/Fyte7D3c7D7
4Q/wWvg6+niGHXfVe7ogY/xPKWI6GGk5dmJ92Gh5IruV1r8htmmeY9dL8FG2
u3dlO8/J5z6j36O09uI0sBT+FXnx3jHopWiA+u5WuyQNHDTFfgeZfuj1sN9F
pYjF4CtiLLiFOMt+P/eeT/H+9xW9XAQuAZMM9RieEwOJhcT9/fW8g+iBcqzF
fYMJe/k3fKOeL0oDN3VUe5DoYfGHqP2q6DHxndR+TfSE+BdLgZuIQS3aQ9s8
/BHvH+p9nqqxp4gml+OOiJf451fYt6g35y/H3fBsayniDbFmjNa8W3Q/NqV7
HlsEvlomfrL4R7DZLOI6Mb1W/INF7HNxFvOZ+7Dah0SPl8OHIRdi35A08DH2
OFLPR4jGif+J5tYXgQ/vUttQhM9emMU4xszR/Nfth89X/+gicNd54huLwG+1
Xpv493EpYjZ31aTno0T36tmiLH7DL8jifbxreRb7Zs8rxD8u/vder4vXxAc+
J7pE9/lgOfzjudg7uKMI30R8XOM4uzOJ8f3d/sFzmxwniWvEuLb2N5fKp9bl
4cMGiv9VHrGFvTzm/Vyivd1XhF4tFT+hiL0gn2bL6LIsMB946XLxjxahPwPE
TypCx5h3v+deIZ3vUoTej1N7j2giviwLnARGulj8vUXo1c+zwHlgvCVZzGH8
T8UPLyIXeN7n7VUKvNnNmPOaLDATuGOl+KfFT8UmOF8RNvpH9c8oIi95J4tn
9D9fRL5ErnSd+qcVgUmWql0iepuzZJHDgPMHZZELgf9Zb7rX/I/6F4t/S/xV
WWBi9oZfeda+BXyNLME560qBj4mDxPA/FBHHvyr+n5LRwVVxjik+C/hotXVg
uvhpjp1DsjgD+++fRU5FfB2YRa6FbYNrVueBbdjjIu/z3xqzUPyb5WgXmH+b
56K54l9X+xokfrbaWaLZ4t9U+wbyFf+3LJ7R/88sntH/98zziRVZ5BLkEYPF
P1GED5/LWNHr4v+RxW/4X2ThE/GHfxX/Ku8uR/uK+Q/Vv1z8vHK0y8z/Nwv5
Ibu14lcWEfPn246QA33HZNH/jvgVReQl/8ri/Jyd3LHedjWftTmz+j7KYg7j
P8jiGf29rJ/Y6N6678+LyO1oPzOfq39jEVgZGU43htzoGLw77qcRa8EVlxvX
gK/q3VdnzDbVc4+vxLqs2aor6MmZ6j87D7x2kfhBeeA19I8xYL1Grw3uvqsc
+A58fYbGn5kHptukM/65iBhLe1wWPFh+SimwKGfa4HOdq7kX5YGVBhl/gSEv
NS7jHf005id54LsRfg4e/5n6L80Db2435j5H7YXqr80Dk4I/zrD/XMW9Iu9y
4OMvjBs/Vf9eeWBE+nY4FvPunj5jN7f0T9C6DeXANPjdffLwvdx3te+8q1ti
4mqN2aL3rvD9tdYb7vC72Msa2zv6hk6vs71jD9Ntv2fpXD/MAy9PtV0j02rz
3MFTxg7EeXLxzs7Hwe7znbOj69sdE9cY26MDPOP95HbganIx8pEd3itn35jF
PXKHG8S/VwQ+Okz7OrAStZaGNOpTYOBD8siNwdMj06hDgTe4n4t8Rw0eC4YA
Y5ADD0zi7oca2wzSGr/JA7NcIX5kHjgLuVxs2WBPzzvGLfO9It9ajR+aB77e
Iw/sstbx8xnH0HVZ5PPk8m00ZksRdRpyxTu81ifk40XUe/bMQ2/QmTmON9h0
uzzGMYa1n7UcZ/hdYPLLtJ/f5oEfwbXsEcy72GcF45E3UuMAH4JDqceBRU/X
3NPzyD/IT7rZpja4ZgeOBVd299wLNH5gHvnH5ix0ET1co7Z3Fph3axa/4dcn
MZd33VqJXHG04xG+AN1oyaI2QZ52ucaMyAPnUnN6qxT1HM7DOUapXVCKnKC9
ZfuC5fup8wpyimrbKOOG+D2cBf3qlYWOETPwIeSez/hOkR2y2mx5ga+JA+Sz
X9O+OlaiRvhmKWIyOn+k+o+rRF2BeN6nEjXQD9T2Fn1d/MQsfCU+ivrPUZWo
AXXX3CMrgZG7iO9UiZyms/hDKlGTO1z8YZWoEVKb6VWJ2ig45NhKYJEjNObr
lcDX2Gl1JWwVfAnO3APbN3+bfRs6gX97OA1fCJal1tW5EnW9AehFHnWXnvZP
2E8P9R1TiXyI+ueJlaiBEofA5WBy9HywdZ2a2RGVqBt209zulcgPqFd1rURN
EGxL7kfO+JLj2NXmwflDnGO+4DHY5nMeR67G3My6MNNjeupdfSuRQ4DZd9fm
SpHPzTVPrjDXc8nVxltXqkrxbvaAv6+1PlGD/WYl6rDUjU+oRO24q97VpRJ5
Um/vmTX+kUYsYj4125MqUbcF175ovX3NY+uSmPeSf8+0/wLzr3c/90Cu9q1K
1JEv1Ht/lkcuArZHhuB7bBcb/q5rKug2cb6fxp6aRWxH9tjnj0yMBwP08Fjs
5U6NvyMPX7vJOoT+POsYwH2doecnZoEdzhJ/Uhbx9gfiv51FHG7VP85YK0x4
YRaxhfrECNcoyH2bnP92KmIcY8hhZmvudUnklyOdY1LnaDRPDQAsPMn1h12u
T1CvoD5Rk8R3ilFen/iGDWx3LkPb3zWQGfarxJDrHVseTcPfE2/I3c+3TyQP
Z93ujkM8J4ZQ3znP/vQ23cOtecQx6gQX2P8+kkY+xDvwF+BKcBH4mPwQ2230
GtjqY2nsn/edn0ftj7ofOvOKdQMsQN0L7LjW9sBZdrm2cq39MXLHn8+y3V1n
nnvu475ZtovZ5hmzphT6xD6neH/4z7fsY/DP5OEDjElGe781xip1xist9u2N
SeCcW4x1wGK3OU5SV7vMGPTJNGIU44aTU+ax9gNqJ+dRgyefxC/fnkQdbuCX
MN+txl7U5GqNC4mx5I6XOK8hB+3nGhHxhtoRNU/qy9TwqAXhM4ix+NE5toU6
15g4O3k6tQTuqsUy5F4OsM0PdO2CGgPywic+7vENOkd9HjYwCmwiGpuGDPBR
w3zPb/veyDf4NnOyiX5iIvGR+hRYEZ/dYL/d3nc+yrF0vvmFnsP4+eZb1+FZ
X689z+8FSz7ks2xKAwvUG3/VG4NN1N4n5IFt+aaDXIiVzcgqjzolZ3rDfnhz
GnUC9vqGz4scJ2WBG8AM4BpqW63YBh4MWed9sv83vSZziWHUA4jp1IWoH9CP
3KgfIDtq4dSEkNMk3yNnp0Z1v8d85rvizjaXok6DjwfPgmupe5AzV1eFX9ya
hl/CP1Fzpz7F/ttVBcbk9xfeP2cabF9GrKROdq91g3rbWOvk6/af6BK+Bh9G
zjLStoW9D7cPYh1q6tSfsM3bdd/D8vCz7IP3Y6MflaK2Ad6nVjfOtrChFPUn
8Cf1P2oS3MtQx2T86ZY08qS7vJcR3g86Qm6NnpATkCtQn6SmmlmHwSVT3E9N
eKjX7FgV98gdgm/IJ8kjDrVtIzu+a1HbeDAJvNjROQjfFKZ5PLGEfYHhr7Yd
19lfUe85LYm7X2yZ4i9H+g5b0sjzOM8Sj0HHiH3InLj8SRq5bKP9XKN9Hb6x
2fq2+7u64xE144m+k21pYNuRfic88rtF8vk19p+G38bGsC+wOjGDeAFuINfC
jhi3yXbHh30wOOPQkU3eJ79XON6g5y22X/AwWKeH/UGL9Wqz56Lz+Fn8LdgH
G95s26Q2gY8Dk/BNlb0SX9Al6omt+gNeGWI8vtZnWW+8SdxhLHPQvXHWReby
7XqOde85r0lspuaALq8zJmR9sB/4bavtnfoRPPELbESNBNzOt7551mHsHtvm
jHyHIT9r/X5J280t/cRvYgJ2iA2C88ilyb82GiuBkajHgQd5L99kwEHENPIm
sEJ32wF6j87znYaYQmxBH6lvo5P4vC0+C3193Y8f2my58B2VMdhSKQ0bQJbY
HHrWaF3dbH3l/eTW4BUwNrK7zlhgo3m+A8ODEfjeBaYg3yf2fNKq52nEYPSC
/1N4yz4TvHmlx6+zbJExuR0YgXsiD2Sv7HOD74y7IwfbVY49Er+32S6WW6fR
X3IvZIkc+dYHbgVH8B2sFfOSh2Eb2AU+mHwLHwJuAD9g39QowVjsCSx+tedS
oyR3QZ+pXSJj5Iuugp3Bxfgbcix8znafr38SMWyr/fwGj2UO3y3BvGfbL96U
/h/XgD3w93zPBCO3YhOwCrGa/78gj+ptHceWsAViwgbbFPvFDtkzsrnZd4LP
u9Fr8i3xetsvfn+LfXWN989ewRkt9nV84+O7IHLhO+oE7wcbJzfmTtBxbAw9
x+/cYD3nrvn2vMqxAnvD1qbZj+OT+Z8aak/Y+y7rJHKnFohskAv4GEwMHub/
BPiWjNyR59GWKf93Q96OL0D+5K7oYEfHjfH2wcR+/PDePjPn5RsaOo3PBgsQ
V7C1pY7D4DpyC7A+OL7Jd0N8q/8SxhnhuyTOgAvAC+Ao8CgY/UbrC3V3dGa9
ZYi/IrcAP7O3sV+KIcTkMd4bciNvRE+xzZn2t+yJHIT34ovBS+QofB9uMA8u
A2vib8HtL1texF9i7bX2IbPsJ6scI4mPfFcc7XiEDMhNOC8YGXyAfwa3glHQ
Q3K4wc7R0Kka2wX/O1DvuTy/wt8gycvIxwY43vf3HPAyOBhfdFQedRNkvtNj
2N9qx1fujTxpjf3LIsfwVkxIzKbmBa5B59A3Yu82xz7iHGdFXhPsy/Bj4LR2
xmr878Ak+40x1jn0rcn3BJ64z7aKnVIbRIeobYKbiGHIm3yBXGKY+qt1rpWV
8OnDvE9wBf/LMNE+AR3nOwnfYvj+C47Fp4Ejdn/j9n1c4zvBZom93Of/AC19
O5o=
"]], PolygonBox[CompressedData["
1:eJwll3m0TmUUxs/9ju8956LQakDINc8kC43yZ4aKtZKxwTzLkBJNyHC5xmS4
10wZG1ctMwkpMkVppRJNCiFpWE2/p+ePZ639+/Z+33POO+y9v7zuQ9oPzkRR
dBwVQyOzUTQEbeDH9TlRNB17AFoD/w4/hd0TbYI3wk+HKBqWRtHyOIomoUa5
UVSX3+pjN2DCJ4l9FG0k/i3iR2H3QMvgd+CJxJ5k/K/ET0dF8FfwZexC9Dz8
JfwL9hT0NGP7oVWM38n4Bfi/wH8J3wI0Dh4Or8CeilrBE+EN2N3ROcYeS6Ko
I2P3M8fV+M5mbf+DnsB+BC3Gfp2Yr/H3QzMZewU9h28Q2or/KP48vrcyqsK3
VkUBuz/xs4gtCU8mtjtaSvxZ4k8Hr5HWpjy6Fd8o4tcQ30NrCD+IXiT+R+LH
Yz+EFsJfwD0ZP4n4jcSO1DfBe+FT2I9LxD6MFhG/jvg2+Cfj34SvJ5oMj4BX
Ys9ABfAp+Dfs2WhR8DfrW4tQS+YaA6/H7ofeZu3G8ttnzP0Oz3iB+EL8+zUX
uh8ugLdh99V8xBahGcQ2Q3dij8a/Dl8fifhp8HbsUagLPBRehj0ETSO+M1rA
2Cs88wT+3Fw/+yrWL4t9nN9KFPMzmhP7ebCvns4M9kLmOxB7D7ckXlOt5Tbi
h2FXyPVelENXsv5N9jH847A7oFnYnzNmNHZvtBLeAk9g/iLm/0jvirYl3gOt
/XZiOuCfjn8HvgHoGXz90RZ8u4mZit0JzYMvwQXYfdEr8GW4F+PzGb+ZsU+g
T4PPmM6Wvnkiz7uJ35LY7ziCsYPReuxFjL8X3xTGb8HfG42GT8AXsSei24l9
Cl6L3Qs9Cw9Eaxm/l/G9iZ+Kfyu+J2Pv/VD0WsZnYAx2H7QZ3q78QPw84j8g
doLWH18vtAL/BfwzsIej1+E/4Hzsjugl+Dz8HOMXMH4fY/NRN3gmvBP7Mb0f
PB/+UGcZtWZsaX67yPifdSfxfRt8F1vgvxEuj4pjl0BvJT6TOotvouvxncx6
rwL+ZvBXWZ+NBnBl+Bj8Blw69l52Yv6Bsff0ZviTrOeqAbeH83jGWp7fOOO7
+UDqd9cd7RgcI5/mOJJ4z7RXH2Scy3ql/jblNOWy3qnXQjlNubZn6rVVzq2q
tWD8bMZeC9fQ2sFz4LJwbd1NeC5cAa6nswrPhyvDt8Bn4L1wHZ0H+Af4fbhp
7LU7De/MeA1vhb+B34MbwxW03vAuuCR8B/xj1t/SPPZdbpf67OtO18U+gn81
/kpwLfgw/DJcHm6ouwoXwtXgxvBR+FW4FtxcuQ5+F24EV4cPwcu1l3AV+CC8
BL5GNQj+WPcRrgLfBn8H74abxD5bXYNzjc7YpMR3XnddazoPro7/utg1oQDO
Cz5LOrPzE9c41TY9sxo8gPtZpPrEGSiCaxBfLnbNW5e4xqq26ptmwFWUr2Ln
AOXatqlzp3KualeP4NyuGjab+Kpwqdg5Ubm0Teq7rZyqu9w6da7XnZ6W+I7p
bukMzIUbMr5l7BrxF3wZ/1HsITl+92r4y8T+hpmJc5Ryk87MysQ5TLlLe7g0
cQ7Q3dceroBrMT4vdo1W7s0PrjXKwVMS1zjVNp3RVXBt/NVj55y7iG8QfHfv
RqsT11zVWu3hErgm/oqxc3A+XFk1IXbNvAyfJ/4Adn/G/A5fhA/Dg3Jca1ul
7gVUcxcm7mnUy+gMvQbXYb66sXNUmeA10toox1Ri7PfE71HvoGcmrlGqTTqz
TZSPiIliP7MpXAbOib3Gj8EVmfNv7O90h+BS+P/N+J0bZd2TqBfZh25InaOU
m5Tj1Rv1SV1r1SNVYq6S8Jwcz3mJ97mHOc6of1APkzjnKtcqh6k2Lw6u7arR
LVKvudb6/zOBPS24FziIrg5eQ63deca3Yq6rgu2zaH/inky9mNZEtbxdcK+g
mr4rcc+nXk85ZGfinki9kO7wnsQ1QrVBOWVq8Dvo2eqhymGXRWnsPd6RuEdT
b7Yj47X9NetarTVWb9M3dS1Wj7M3cc1WrVaO+jBxjVVtVQ64kvib9C3ntAeJ
e171usqBJYLPlM7STxmvbfFgW2v8Z+IapNpzIeN3/Trrd9M7qxaOCa61qomq
pfcF9z6qqeodC4n/PuMeUr3U+ODeVT3V+cRnRmdFMXVS53Tlct0B1cJngntv
1cSmqXsg9T7qwZukzvHK7TrT9VPXAOV+3VH13l1T13b14OoFu6XuxdQTqvfu
krr3UA+u3qFz6t5TPUSj1DlbuVp3+KbUd0R3QznqUOKeQr2Eaoxq+9jgXl41
vmLqGqLaoRxYLXVNUy1Tzj3O+JLBe9OJOS5k/Zvsg+rJsEsFr33nHPc6C4P/
O6jn0d36OetY3TH1apOC/2uoZ1Nv1Ta491GP9UvWc2quI8Tnpe4BVPuVE9VL
Fwb/11BPXTN1zVWtVY7Xf4vc4Lun/xjKBZeynks5Qb176+BeXz287u5PWd91
3eH/ANAH02c=
"]]}]}}],
AspectRatio->1,
Axes->None,
Frame->True,
PlotRange->{{-3, 3}, {-10, 10}},
PlotRangeClipping->True,
PlotRangePadding->{
Scaled[0.02],
Scaled[0.02]}]\)

Hello Kyle, I enjoyed reading through you blog. Unlike Rahul, I am kinda unfamiliar with the experiment so a brief description of the procedure would have made it much clearer for me. Also, you have taken the fourier transforms of these shapes. but they appear to be in 2D. is there another dimension in the z direction that I’m not seeing? or are the shapes simply rectangles and you are only investigating their orientation instead of their volume?
great read
Peace
Hey Kyle. I like your simulations. I think its impressive how you’ve tried to use unit step functions to create all your functions, because it doesn’t seem easy.
I am wondering why there are these white bands that separate your functions into many different rectangles. Is this just how mathematica represents sums of step functions or are those actually regions that get light?
Also, I have a few recommendations regarding the problems you stated. You said you had problems plotting the imaginary outputs. I think you will be able to plot them if you plot the Real Parts and the Imaginary Parts of the Fourier Transforms separately. Also, try plotting the Amplitude of the Transforms because this takes both the Real and Imaginary parts into account and it represents the actual diffraction pattern. And as for the problem you had making angled shapes, maybe Mathematica’s drawing tool could work. http://reference.wolfram.com/mathematica/guide/GraphicsInteractivityAndDrawing.html
It was interesting going through your results. Good luck !
-Rahul