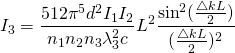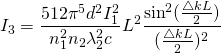Category Archives: Tariq

Limitations of High efficiency

The efficiency of the wave mixing process decreases as $|\bigtriangleup k|L$ increases( although there are some fluctuations). This is becuase when L gets greater than $\frac{1}{\bigtriangleup k}$ the harmonic wave can get out of phase with incident beam and power can flow from the $\omega_{2}$ back into the 2 $\omega_{1}$ waves. The coherence length of the interaction  is $L_{c}=\frac{2}{\bigtriangleup k}$ so the phase mismatch factor can be written as $sinc^{2}(\frac{L}{L_{c}})$

From the phase mismatch plot we see a big decrease in efficiency when $\bigtriangleup k \neq 0$ is not satisfied. This is quite difficult to obtain in labs because the refractive index of materials that are lossless in the range $\omeg_{1}$ to $\omega_{2}$ have normal dispersion when $\frac{dn}{d\lambda}<0$. The refractive index is an increasing function of frequency. For the case of second harmonic $n\omega_{1} = n\omega_{2}$, this is not possible since $n(\omega)$ increases with $\omega$. So what is generally used is birefringence of crystals ie.the dependence of the refractive index on the direction of polarization of the optical radiation. This slows down out of phase waves to get a perfect mismatch.

Share

Derivation of Transmitted Wave Equation

(1)   \begin{equation*} \bigtriangledown \times \bigtriangledown \times \widetilde{E}_{n} + \frac{\epsilon^{(1)}(\omega_{n})}{c^{2}} \bullet \frac{\partial^2 \widetilde{E}_{n}}{\partial t^2} = \frac{-4\pi}{c^2} \frac{\partial^2 \widetilde{P}^{NL}_{n}}{\partial t^2} \end{equation*}

$\widetilde{P}^{NL}_{n} =$ Non-Linear part of Polarization Vector

$ \widetilde{E}_{n} =$ Electric Field vector

$\epsilon^{(1)}(\omega_{n}) =$ Frequency dependent dielectric Tensor

Equation (1) is derived from Maxwell’s equation and is the equation for waves in medium. It is valid for each frequency component of the field.

$\widetilde{E}_{2}(z,t) =A_{2}e^{i(k_{2}z-wt)},   \widetilde{P}_{j}(z,t) =P_{j}e^{-i\omega_{j}t},$    $P_{1} =4dA_{2}A^{*}_{1}e^{i(k_{2}-k_{1})z}, P_{2} =2dA^{2}_{1}e^{i2k_{1}z}$

$\widetilde{E}_{2}(z,t)$ will be my equation for the transmitted wave at frequency  propagating in the z direction,$ \widetilde{P}_{2}(z,t)$ the nonlinear source term and $P_{2}, P_{1}$  the amplitude of the nonlinear polarization and amplitude of incident beam respectively.

(2)   \begin{equation*} -\bigtriangledown^{2} \widetilde{E}_{n}-\frac{\omega^{2}_{n}}{c^{2}}\epsilon^{(1)}(\omega_{n}) \bullet \widetilde{E}_{n}= \frac{4\pi \omega^{2}_{n}}{c^2} \widetilde{P}^{NL}_{n}} \end{equation*}

$\bigtriangledown^{2}$ can be replaced with $ \frac{\partial^2}{\partial z^{2} }$

(3)   \begin{equation*} \frac{\partial^2}{\partial z^{2}}\widetilde{E}_{2}= \frac{\partial}{\partial z} [ \frac{\partial A_{2}}{\partial z}e^{i(k_{2}z-wt)} +ik_{2}A_{2}e^{i(k_{2}z-wt)}] \end{equation*}

(4)   \begin{equation*} \frac{\partial^2}{\partial z^{2}}\widetilde{E}_{2}= [ \frac{\partial^{2} A_{2}}{\partial z^{2}} +ik_{2}\frac{\partial A_{2}}{\partial z}+ ik_{2} \frac{\partial A_{2}}{\partial z} -k^{2}_{2}A_{2}]e^{i(k_{2}z-wt)} \end{equation*}

So the wave equation becomes

(5)   \begin{equation*} -[ \frac{\partial^{2} A_{2}}{\partial z^{2}} + 2ik_{2} \frac{\partial A_{2}}{\partial z}-k^{2}_{2}A_{2}]e^{i(k_{2}z-wt)} -\frac{\omega^{2}_{2}}{c^{2}}\epsilon^{(1)}(\omega_{2})A_{2}e^{i(k_{2}z-wt)} =\frac{4\pi \omega^{2}_{n}}{c^2}\bullet2dA^{2}_{1}e^{i(2k_{1}z-\omega_{2}t)} \end{equation*}

(6)   \begin{equation*} -[ \frac{\partial^{2} A_{2}}{\partial z^{2}} + 2ik_{2} \frac{\partial A_{2}}{\partial z}-k^{2}_{2}A_{2} -\frac{\omega^{2}_{2}}{c^{2}}\epsilon^{(1)}(\omega_{2})A_{2}]e^{i(k_{2}z-wt)} =\frac{8\pi \omega^{2}_{2}}{c^2}dA^{2}_{1}e^{i(2k_{1}z-\omega_{2}t)} \end{equation*}

$k^{2}_{2}= \frac{\omega^{2}_{2}}{c^{2}}\epsilon^{(1)}(\omega_{2})$ hence

(7)   \begin{equation*} [ \frac{\partial^{2} A_{2}}{\partial z^{2}} + 2ik_{2} \frac{\partial A_{2}}{\partial z}]e^{i(k_{2}z-wt)} =-\frac{8\pi \omega^{2}_{2}}{c^2}dA^{2}_{1}e^{i(2k_{1}z-\omega_{2}t)} \end{equation*}

replace $ \frac{\partial}{\partial}$ with $\frac{d}{dz}$ because $A_{2}$ is only a function of $z$ and with the slowly-varying-amplitude approximation $|\frac{d^{2}A_{2}}{dz^{2}}|<<|k_{2}\frac{aA_{2}}{dz}|$ hence we get

(8)   \begin{equation*} \frac{dA_{2}}{dz}= \frac{4 \pi id \omega^{2}_{2}}{k_{2}c^{2}}A^{2}_{1}e^{i\bigtriangleup kz} \end{equation*}

Share

Preliminary Results

I modeled the effect of $\bigtriangleup k$ using the equation:

(1)   \begin{equation*} I_{3} = \frac{512\pi^{5}d^{2}I_{1}I_{2}}{n_{1}n_{2}n_{3}\lambda^{2}_{3}c}L^{2}\frac{\sin^{2}(\frac{\bigtriangleup kL}{2})}{(\frac{\bigtriangleup kL}{2})^{2}} \end{equation*}

2.2.20 Nonlinear optics Robert W.Boyd

This can be simplified to $I_{3} = I_{3}(max)\frac{\sin^{2}(\frac{\bigtriangleup kL}{2})}{(\frac{\bigtriangleup kL}{2})^{2}}$

Fig 2.2.2 Nonlinear optics Robert W.Boyd

Link to mathematica code https://vspace.vassar.edu/tasanda/sinc.nb

It shows the harmonic generation output as a function of the phase match $\bigtriangleup k$ when $\bigtriangleup k \sim 0$

Link to mathematica code https://vspace.vassar.edu/tasanda/Manipulation.nb

This model shows the effect of superposition of waves and explains why intensity is largest when $\bigtriangleup k=0$

Deriving Efficiency

Solving the general wave equations for the two frequencies $\omega_{1}$(incident) and $\omega_{2}$(Second harmonic) we obtain coupled-amplitude equations.

(2)   \begin{equation*} \frac{dA_{1}}{dz}= \frac{8 \pi id \omega^{2}_{1}}{k_{1}c^{2}}A_{1}A_{2}e^{i\bigtriangleup kz} \end{equation*}

(3)   \begin{equation*} \frac{dA_{2}}{dz}= \frac{4 \pi id \omega^{2}_{2}}{k_{2}c^{2}}A^{2}_{1}e^{i\bigtriangleup kz} \end{equation*}

2.6.10, 2.6.11 Nonlinear optics Robert W.Boyd

Where $\bigtriangleup k = 2K_{1}-k_{2}$ is the wave vector mismatch. Integrating these equations gives us

$A_{1}=(\frac{2\pi I}{n_{1}c}) u_{1}e^{i\phi_{1}},       A_{2}=(\frac{2\pi I}{n_{2}c})u_{2}e^{i\phi_{2}$

2.6.13, 2.6.14 Nonlinear optics Robert W.Boyd

The new field amplitudes $u_{1}$ and  $u_{2}$ are defined such that $u_{1}(z)^{2} + u_{2}(z)^{2} = 1$(conserved normalized quantity). Next we introduce a normalized distance parameter

$\zeta=\frac{z}{l}$     where      $l=(\frac{n^{2}_{1}n_{2}c^{3}}{2\pi I})^{\frac{1}{2}}\frac{1}{8\pi \omega_{1} d}$

2.6.18, 2.6.19 Nonlinear optics Robert W.Boyd

$l$ is the distance over which the fields exchange energy.

$\frac{du_{1}}{d\zeta}=u_{1}u_{2}sin\theta$ and $\frac{du_{2}}{d\zeta}=-u^{2}_{1}sin\theta$.

2.6.22, 2.6.23 Nonlinear optics Robert W.Boyd

If we assume $cos\theta=0$ and  $sin\theta=-1$ the equations simplify to  $\frac{du_{1}}{d\zeta}=-u_{1}u_{2}$   and   $\frac{du_{2}}{d\zeta}=u^{2}_{1}$

2.6.31, 2.6.32 Nonlinear optics Robert W.Boyd

The second equation can be written as $\frac{du_{2}}{d\zeta}=1-u^{2}_{2}$(from conservation).

Hence $u_{2}=tanh(\zeta+ \zeta_{0})$. Initially we assume there is only the incident beam and no harmonic generation hence $u_{1}(0)=1, u_{2}(0)=0$. Therefore $u_{2}= tanh\zeta$ and  $u_{1}=sech\zeta$. Plotting these two equations below shows that incident waves are converted into the second harmonic.

Fig 2.6.3 Nonlinear optics Robert W.Boyd

Link to mathematica code https://vspace.vassar.edu/tasanda/u1u2.nb

The efficeincy $\eta$ for the conversion of power from incident wave $\omega_1$ to $\omega_{2}$ is

(4)   \begin{equation*} \eta= \frac{u^{2}_{2}(L)}{u^{2}_{1}(0)} \end{equation*}

2.6.43 Nonlinear optics Robert W.Boyd

From the diagram it seems like increasing the medium length will increase the amplitude but doing so is not practical. Generally a higher pump intensity leads to a larger $\eta$ except to the limit of very high conversion efficiency.

Taking an example of a medium of 1cm length, the efficiency equals $tanh^{2}(1)$ which is $58\%$

 

Share

Project Plan

Second Harmonic Generation is a special case of optical mixing. It is a process by which photons from a laser beam are mixed in a nonlinear medium and the output photon has double the energy and frequency and half the wavelength. Conditions satisfy $\omega_{1}=\omega_{2}=\omega$ and $\omega_{3}=2\omega$. Both energy and momentum conservation must be satisfied. Energy by $\omega_{3}=\omega_{1}=\omega_{2}$ and momentum by $k_{3}=k_{1}+ k_{2}$

In more detail:
“Nonlinear optics is the study of phenomena that occur as a consequence of the modification of the optical properties of a material system by the presence of light”. Input waves are at frequencies $\omega_{1}$ and $\omega_{2}$. By the nonlinear effects of incident beams (at the atomic level) each atom develops an oscillating dipole moment which contains a component at frequency $\omega_{1}+\omega_{2}$. Each atom radiates this frequency but there are many atoms in our medium and hence many atomic dipoles oscillating with a phase determined by the phases of the incident waves. When the relative phasing matches the waves radiated by each dipole will add constructively turning the system into a phased array of dipoles. When this happens the electric field strength of the radiation emitted will be the number of atoms times larger and hence the intensity will be the number of atoms squared.

I will assume my system to be lossless and dispersion-less for simplifying equations

(1)   \begin{equation*} \bigtriangledown \times \bigtriangledown \times \widetilde{E}_{n} + \frac{\epsilon^{(1)}(\omega_{n})}{c^{2}} \bullet \frac{\partial^2 \widetilde{E}_{n}}{\partial t^2} = \frac{-4\pi}{c^2} \frac{\partial^2 \widetilde{P}^{NL}_{n}}{\partial t^2} \end{equation*}

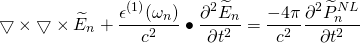
2.1.19 Nonlinear optics Robert W.Boyd

$\widetilde{P}^{NL}_{n} =$ Non-Linear part of Polarization Vector

$ \widetilde{E}_{n} =$ Electric Field vector

$\epsilon^{(1)}(\omega_{n}) =$ Frequency dependent dielectric Tensor

Equation (1) is derived from Maxwell’s equation and is the equation for waves in medium. It is valid for each frequency component of the field.

$\widetilde{E}_{2}(z,t) =A_{2}e^{i(k_{2}z-wt)},   \widetilde{P}_{j}(z,t) =P_{j}e^{-i\omega_{j}t},$    $P_{1} =4dA_{2}A^{*}_{1}e^{i(k_{2}-k_{1})z}, P_{2} =2dA^{2}_{1}e^{i2k_{1}z}$

2.2.1, 2.2.3, 2.2.4,2.2.5, 2.2.7  Nonlinear optics Robert W.Boyd

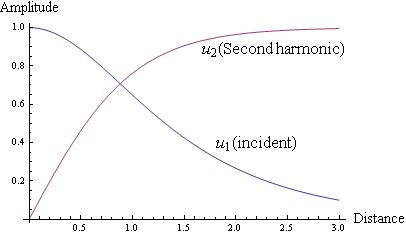
$\widetilde{E}_{2}(z,t)$ will be my equation for the transmitted wave at frequency  propagating in the z direction,$ \widetilde{P}_{2}(z,t)$ the nonlinear source term and $P_{2}, P_{1}$  the amplitude of the nonlinear polarization and amplitude of incident beam respectively. I will make diagrams of incident waves hitting the medium and resulting transmitted wave.

Substituting the transmitted wave equation in the wave equation and solving by hand I will find coupled amplitude equation.

(2)   \begin{equation*} \frac{dA_{2}}{dz}= \frac{4 \pi id \omega^{2}_{2}}{k_{2}c^{2}}A^{2}_{1}e^{i\bigtriangleup kz} \end{equation*}

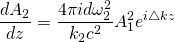
2.6.11 Nonlinear optics Robert W.Boyd

$\bigtriangleup k = k_{1}+k_{1}-k_{2}$ is the wave vector mismatch

2.6.12 Nonlinear optics Robert W.Boyd

$A_{i} =$ amplitude of the wave

The coupled amplitude equation shows how the amplitude of $\omega_{2}$ wave varies due to it’s coupling of two $\omega_{1}$ waves. And from this we can find intensity, which is more useful.

    \begin{displaymath} I_{i} = \frac{n_{i}c}{2\pi} |A_{i}|^{2} \end{displaymath}

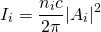
(3)   \begin{equation*} I_{3} = \frac{512\pi^{5}d^{2}I^{2}_{1}}{n^{2}_{1}n_{2}\lambda^{2}_{2}c}L^{2}\frac{\sin^{2}(\frac{\bigtriangleup kL}{2})}{(\frac{\bigtriangleup kL}{2})^{2}} \end{equation*}

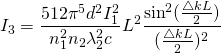
2.2.17, 2.20 Nonlinear optics Robert W.Boyd

Where $\lambda_{2}=\frac{2\pi c}{\omega_{2}}$ , L is the length of the medium and d is the tensor

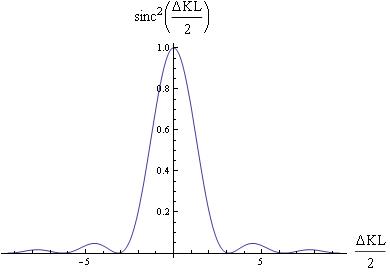
I will try and model the effect of $\bigtriangleup k$ of the wave vector on the efficiency and take special notice when $\bigtriangleup k=0$ since this is the condition for perfect phase matching. I will make an animation to vary $(\frac{\bigtriangleup kL}{2})$  in the intensity equation and this will show the effects of wave vector mismatch on the efficiency of harmonic-generation.

I will also attempt to model the effects of absorption.

As an example I will use the nonlinear media KDP (Potassium Dihydrogen Phospate) crystal to model second harmonic generation for a laser beam at $1.06\mu$ meters. KDP is widely used in commercial Non linear optical materials because of its electro-optic effects and it’s high non-linear coefficients.

REFERENCES:

Boyd. Nonlinear Optics. New York:  Academic Press, 1992

SHEN. The Principles of Nonlinear Optics. New York:  Wiley-Interscience, 1984

 

Share

Second Harmonic Generation

My research project is modeling Second Harmonic Generation. It is a process by which photons from a laser beam are mixed in a nonlinear medium and the output photon has double the energy and frequency and half the wavelength. I will model the conversion efficiency, and the different types of phase matching. Second Harmonic Generation relates to certain topics in our course such as chapter 9 of Griffiths on absorption and dispersion of EM waves and topics from chapter 11 on radiation. Applications of frequency mixing are found in the use of radio waves in extending the tunable range of shorter wavelengths.

Share