Learned:
- to measure/ record an optical setup
- what to do when the setup does not actually function
- to clean optics
- to pick worms.
This week was the first real week in the lab where I could help instead of being lost.
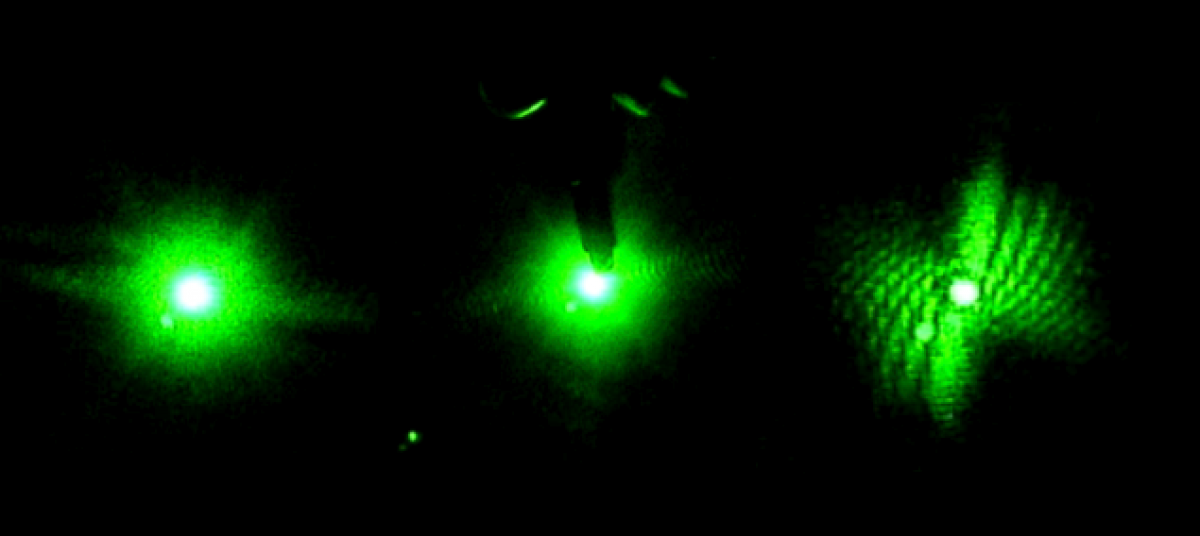
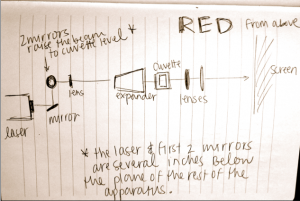
1) Measuring a setup: Hold a piece of string taught between your fingers. Making sure it is parallel to the table, hold one end directly above the center of the laser lens, and pinch the string directly above the first obstacle (pinhole, lens, etc). Mark the distance with a marker, and measure against a ruler. Record and repeat. Below is an image from my notebook, drawn on 2/13/14, of the Helium-Neon laser setup (from above).
2) What to do when the setup is not aligned: The laser work table is sturdy and covered in a grid of holes, into which instruments can be secured. If the instruments are not in alignment, the laser will not reach through all of the lenses, etc, to reach the screen. To adjust, simply line up the instruments against one of the straight lines of drill holes. Most instruments will either be in a straight line or at right angles to each other.
3) Cleaning optics: Cleaning the mirrors and lenses is essential to get a clear image projected on the screen. To clean: place the mirror on a paper towel (that material does not really matter). Take a piece of lens paper, being careful to touch it as little as possible. Fold it, using the small forcep clamps, until a clean edge can be secured with the forceps. Wet the paper with a drop or two of methanol, and wipe slowly across the mirror, making sure not to touch the mirror with the same section of paper more than once.
4) Picking worms: First, retrieve a 4-day old (mature) dish of C.elegans worms, and a new dish with food (E.coli). Pick a Pick (a glass rod with a tiny wire of on the end). Using the dissecting microscope and a bunsen burner (to sanitize the pick between each contact), move four or five worms from the old plate to the new one. This is difficult at first because depth perception through a microscope takes practice and patience. Try not to kill any worms. Then wrap the dishes, mark them “VAOL” and the date, and place back in the refrigerator for four more days.
In conclusion: Some big strides were taken in the lab for me this week. I am looking forward for the data collection process, which is scheduled to begin on Monday (2/17).