Before introducing the concept of oversampling, let’s first talk about an effect named “aliasing” that is just as important.
Aliasing

An example of aliasing can be seen in old movies, especially when watching wagon wheels on old Western films. You would occasionally see the wheels as if they going in reverse. This phenomenon occurs as the rate of the wagon wheel’s spinning approaches the rate of the sampler (the camera operating at about 30 frames per second).
The same thing happens in data acquisition between the sampler and the signal we are sampling.
Nyquist Theorem
A theorem that states the relationship between the acquired data and sampling frequency (rate of sampler) is stated as the Nyquist Theorem. It states that 2 samples per “cycle” of input signal is needed to define it the input signal. Thus, a signal with frequency f can be accurately measure as long as you are sampling it at greater than 2f.
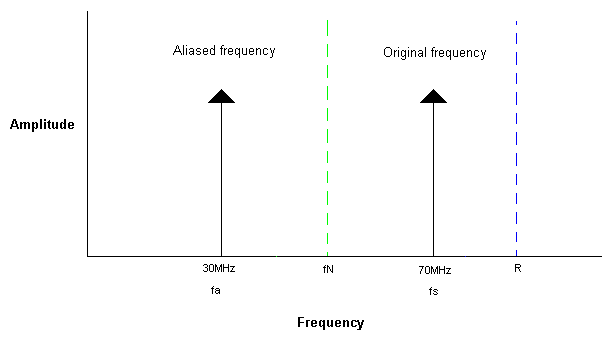
The following picture is a Frequency versus amplitude plot showing an aliased signal, fa, which occurs due to “aliasing back” from the original signal of 70MHz where
R (sampling rate) = 100MS/s
fs (signal being sampled = 70MHz
fN (the Nyquist frequency) = 50MHz
fa (aliased frequency) = 30MHz
Oversampling a signal
Applying the concept of Nyquist Theorem, we can see that oversampling is sampling at a rate beyond twice the highest frequency component of interest in the signal and is usually desired. Because real-world signals are not perfectly filtered and often contain frequency components greater than the Nyquist frequency, oversampling can be used to increase the foldover frequency (one half the sampling rate) so that these unwanted components of the signal do not alias into the passband.
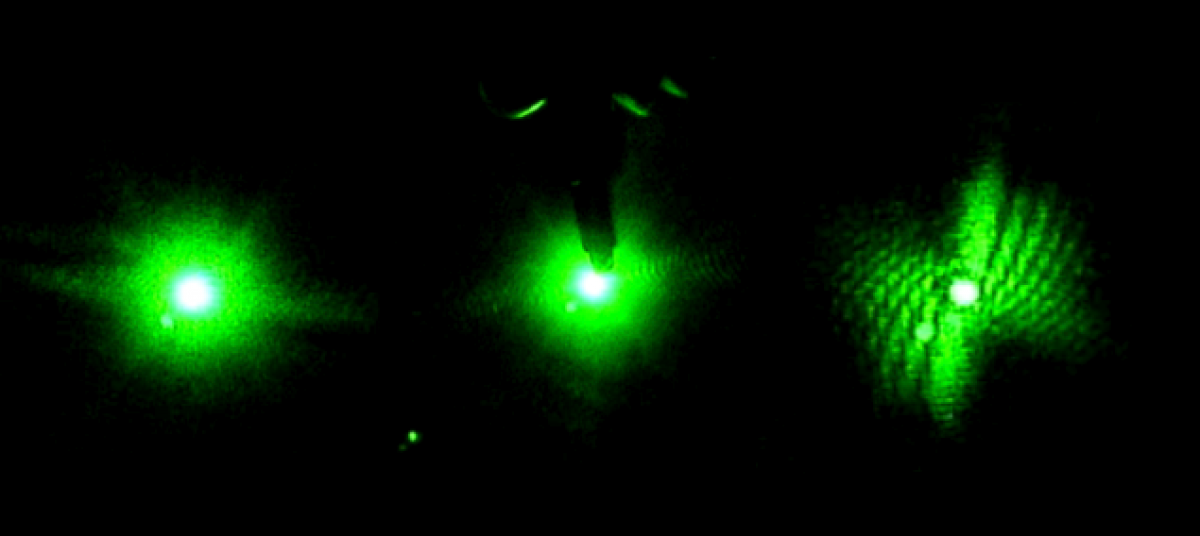
Oversampling an object through diffraction
In the case of sampling an object, the Nyquist frequency becomes the inverse of the size of the diffracting specimen, and the sampling rate is the laser frequency. As suggested in the last post, reconstruction of an image through its diffraction pattern is a very important subject in our current research, and “the phase problem” that was introduced will be closely tied to the the Nyquist Theorem, where the diffraction pattern of a finite specimen has to be more finely sampled than the Nyquist frequency.
According to the oversampling phase method, the method above corresponds to surrounding the electron density of the specimen with a no-density region. When the no-density region is bigger than the electron-density region, sufficient information is recorded so that the phase information can in principle be retrieved from the oversampled diffraction pattern.
Reference Cites:
yoksis.bilkent.edu.tr/pdf/10.1364-AO.39.005929.pdf