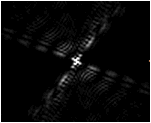
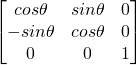Symmetry Library

Symmetry patterns  of group “C”

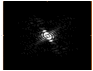
Symmetry Group C∞: This is an image of C. elegans in a circular shape. Once taken, the image is imported into Mathematica, where a specific code is used to form the diffraction image. Examining the diffraction image, we can conclude that  it has a linear element, which contains an Inversion Center. Thus the diffraction image possesses symmetry by using the rules of Group theory. This symmetry can be classified under the C infinity group. The matrix is composed from the diffraction image.

 C. elegans                                Diffraction Image

                           

matrix 

\begin{bmatrix} cos\theta & sin\theta &0 \\ -sin\theta & cos\theta & 0\\ 0& 0 &1 \end{bmatrix}

 

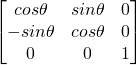
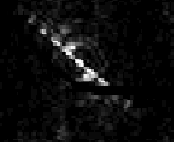
Symmetry Group C1:  Once an image of the C. elegans is taken, the image is imported into Mathematica, where a specific code is used to form the diffraction image. This diffraction image is classified under the symmetry group C1. This is interpreted as a nonlinear element that doesn’t contain multiple c3, a reflection plane, or proper rotational axis. The diffraction image also does not contain an inversion center. Examining the diffraction image, we can conclude the C. elegans has a unique shape that is classified under diffraction image from the C. elegans possessive symmetry by using the rules of symmetry under Group theory. This symmetry can be classified under the C1. The matrix is composed from the diffraction image.

 

C. elegans                                   Diffraction Image

matrix

\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0\\ 0& 0 &1 \end{bmatrix}

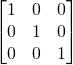
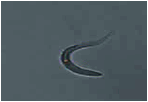
Symmetry Group C2v:  The C. elegan shown below is in shape in a classical “C” shape. The image is imported into Mathematica where a specific code is used to form the diffraction image. Examining the diffraction image we can conclude the diffraction image from the C. elegan possessive symmetry by using the rules of symmetry under Group theory. The diffraction pattern from the C. elegan has a linear element that does not include multiple C3 or horizontal perpendicular axes. However it does contain a proper rotational, and vertical reflection plane. This symmetry can be classified under the C2v group. The matrix is composed from the diffraction image.

C. elegans                                   Diffraction Image

           

matrix

 

\begin{bmatrix} 1 & 0 &0 \\ 0&-1 & 0\\ 0&0 &1 \end{bmatrix}

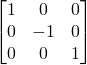
Symmetry Group C2: This is an image of a C. elegan in a sinusoidal shape. Once taken, the image is imported into Mathematica where a specific code is used to form the diffraction image. Examining the diffraction image we can conclude it has a linear, that element that does not include multiple C3 or horizontal axis perpendicular axes. However, it has a proper rotational and vertical reflection plane. Thus the diffraction image possesses symmetry by using the rules of Group theory. This symmetry can be classified under the C 2 group. The matrix is composed from the diffraction image.

C. elegans                                   Diffraction Image 

           

Matrix

\begin{bmatrix} -1 & 0 &0 \\ 0 &-1 & 0\\ 0& 0 &1 \end{bmatrix}

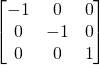
Symmetry pattern of  Group “D”

Symmetry Group D∞: This is an image of a C. elegan in a linear shape. Once taken, the image is imported into Mathematica where a specific code is used to form the diffraction image. Examining the diffraction image we can conclude it has a linear element, which contains an Inversion Center. Thus the diffraction image possesses symmetry by using the rules of Group theory. This symmetry can be classified under the D infinity group. The matrix is composed from the diffraction image.

C. elegans                                   Diffraction Image 

          

Matrix

\begin{bmatrix} cos\theta & sin\theta &0 \\ -sin\theta & cos\theta & 0\\ 0& 0 &1 \end{bmatrix}