“C. elegans has become a favorite model system for the study of development due to the recent discovery that its genetic makeup differs very little from that of a fly, fish, mouse, or human.”
–Professor Greg Hermann
C. Elegans.
I never actually thought that such small creature could still draw so much attention from a variety of disciplines nowadays. Because of their simple neuron structures and direct corresponding movements in the water, their behaviors are of interest to neuroscience, biology, and just recently through our studies–physics.
Why is it related to physics all of a sudden?
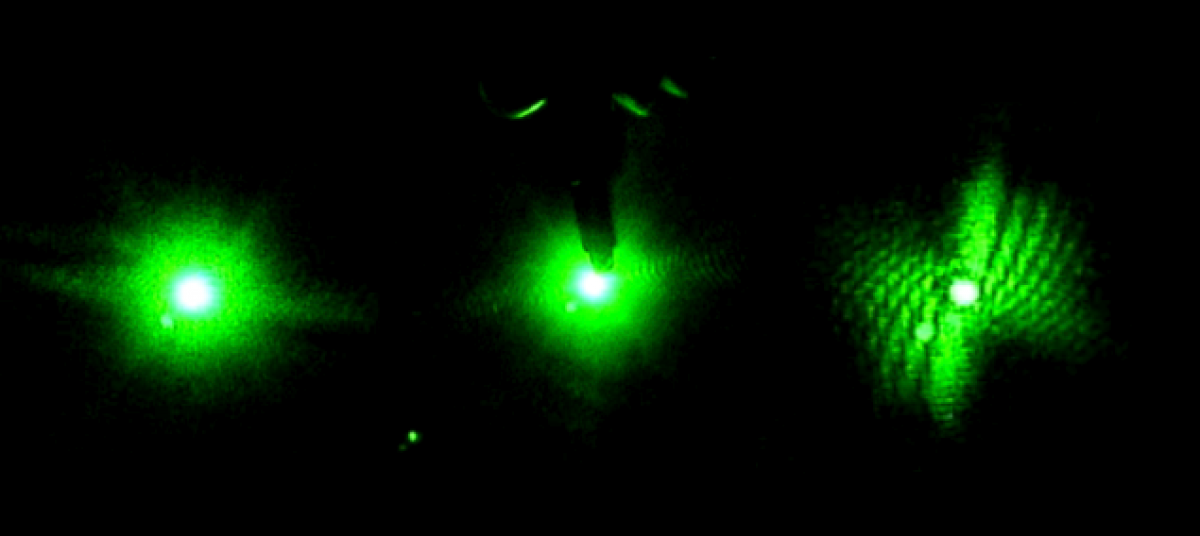
Here is the reason–lasers are great motion detectors since their travel paths are very accurate and any small alterations in movements can be reflected in pattern changes in laser.
Thus, one important component of this research is to carry out the laser diffraction for the movements of C. elegans in a curvette and record their patterns while they are allowed to freely swim in three dimensions. The advantage of such observations, compared to using a microscope, is that the C. elegans are allowed to freely move about instead of being restricted to two dimensions in Petri dishes under the microscope.
So far, the diffraction patterns have been analyzed to understand the frequency of the worm’s movement and how its movement is affected by its environment. The experiment then moved to a higher stage which is allowing for the Fourier transform of the original diffraction pattern. Fourier transform allows very scattered and different patterns to be expressed very uniformly through similar terms. Thus, we now have the worm and the diffraction patterns of its movements.
Where are we looking forward to going with all this?
Of course, we all know the common phase problem with the Fourier transform analysis, where phase information of the original pattern is lost, which is exactly what happened to our Fourier transform results. Thus, by comparing the Fourier transform results and the real image of the worm moving at that precise moment, we can gather more info regarding the operational methods of the transform.
In the end, we hope to retrieve the phase information of the transform, and eventually be able to predict the original shape of the worm movement. Currently, we are able to reconstruct a small section of a worm. The general shape of the worm has been quite successfully outlined, even thought the location of the worm is not exactly correct.
We have much to hope in this line of pursuit. We will go on to try retrieving the phase information of the worm movement, and discover better algorithms to return the diffraction patterns to its original image. Moreover, we’re hoping that in the future, a 3-dimensional analysis of the movement of the worm is possible through laser diffraction. This way, the advantage of the Fourier transformation method can more clearly demonstrate its effectiveness and large potential in the field of biology and related observational sciences.