This summer I worked with Professor Rebelein in the economics department on his project called “Assessing the Distributional Effects of Alternative Health Insurance Programs”, continuing the work we started this past academic year. The goal of this research is to create a mathematical model of health care choices so that the potential welfare impacts of different health care policies can be analyzed, especially how welfare varies for different income groups. Given the upcoming election, health care policy issues are at the forefront of public consciousness, so I was very excited to be working on this project.

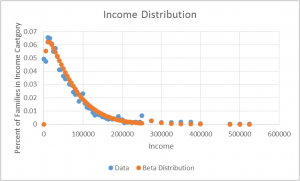
The first thing we did was find income and medical expenditure distributions from Medical Expenditure Panel Survey data to get parameters for the mathematical model. This image shows our beta distribution fitted to the actual distribution of income taken from the data.

Most of the summer was spent reviewing the current literature on health care simulation models. Many other researchers, most notably Jonathan Gruber from MIT, and organizations like the Urban Institute have created their own models of health care and insurance demand, and I spent a lot of time looking at how these models worked and the math behind them. Professor Rebelein wanted to have health status, which is how healthy someone is, included as a factor into consumers’ decision making. Because none of the major models have included health status as a factor, I also spent time reading about utility models that include health status. After reviewing the current research we were able to finalize a model of consumer utility incorporating health state.

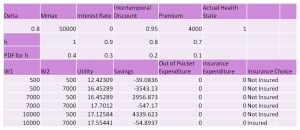
I spent the rest of the time writing a function in the R programming language that would solve our model for different parameters like income and insurance premiums. It was a challenge because the model has to predict consumers’ insurance and health care spending choices for a number of different scenarios. Each case has to be written separately into the function. The model is a two period model. Given a certain income in each time period, consumers must choose how much to save or borrow and whether or not to buy health insurance given their expected well being. In the second time period people must choose whether or not to pay their medical bills, which are determined by their health state, based on whether they can afford them or whether they will be better off staying sick but having more money. This image shows what the output of this function looks like in an Excel format.

I’m very thankful for the opportunity to do summer research through the Ford program, and I’ve learned a lot through the process.