I have to admit, there was a time when I was in love with an equation.
The class of nonlinear differential equations are fairly notoriously pains in the butt, but for me, they represented something other than that pain. They reflected the artful beauty found in integral calculus. Sergey Lvin, was a soft spoken mathematics professor at the University of Maine who took pride in his teaching. I recall asking him once why my differential equations class was so difficult while derivatives were really automatic and straightforward. He smiled and said to me that “Differentiation was a science and integration was an art.” What he meant was that one could follow the rules by rote and take the derivative of any function imaginable, and yet to find the integral of a function was often a journey through considering various solution tactics. And to make matters worse, differential equations are implicit relationships between derivatives and the state quantities. Rather than ![]() we have that
we have that ![]() and that makes all the difference in the world.
and that makes all the difference in the world.
However, utilizing the tools you’ve learned with the experience you’ve gained to approach problems, often from oblique lines of inquiry, is the joy of mathematics. I enjoyed learning methods, building my tools belt to handle any situation, and this is in part why I remember liking the Verhulst equation so much:
(1) ![]()
Pierre Verhulst was a mathematician of some note from the early 19th century. In a collection of papers starting in 1938 (of which I must get my hands on) he proposes that for a population of ![]() individuals at time
individuals at time ![]() that there is some intrinsic growth rate to the population,
that there is some intrinsic growth rate to the population, ![]() , and a natural carrying capacity for it within its environment,
, and a natural carrying capacity for it within its environment, ![]() . It took him 7 years to call the solution to this differential equation the logistic equation and some how the wires crossed and that is what I see the differential equation called. If you look close then you can show that for
. It took him 7 years to call the solution to this differential equation the logistic equation and some how the wires crossed and that is what I see the differential equation called. If you look close then you can show that for ![]() and
and ![]() we can approximate the logistic growth equation with
we can approximate the logistic growth equation with
(2) ![]()
which is the only differential equation that I know the solution to ![]() so mathematically
so mathematically ![]() matches that biological meaning of growth rate. Furthermore, for
matches that biological meaning of growth rate. Furthermore, for ![]() the logistic growth equation results in a growing population (
the logistic growth equation results in a growing population (![]() ) for all
) for all ![]() gives credence to the interpretation that
gives credence to the interpretation that ![]() is the carrying capacity. This was amazing to me. Here was a fairly complex (for me at the time) differential equation where the parameters just made sense. To boot it was an adventure to solve. Recall that
is the carrying capacity. This was amazing to me. Here was a fairly complex (for me at the time) differential equation where the parameters just made sense. To boot it was an adventure to solve. Recall that
(3) ![]()
but now the left hand-side is just a mess. This is where the art comes in.
We note that ![]() (when did you learn partial fraction decomposition? I cannot recall when I was supposed to have and Eisso Atzema – my professor for some course requiring said knowledge – liked to tease me for my inability to recall said information. Is it he who I first gained math related snarkiness from?). The integral of each of these parts is trivial at this point, let me be pendantic for anyone not cruising along:
(when did you learn partial fraction decomposition? I cannot recall when I was supposed to have and Eisso Atzema – my professor for some course requiring said knowledge – liked to tease me for my inability to recall said information. Is it he who I first gained math related snarkiness from?). The integral of each of these parts is trivial at this point, let me be pendantic for anyone not cruising along:
(4) 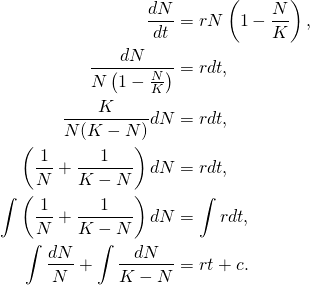
Now use ![]() -substitution:
-substitution:
(5) 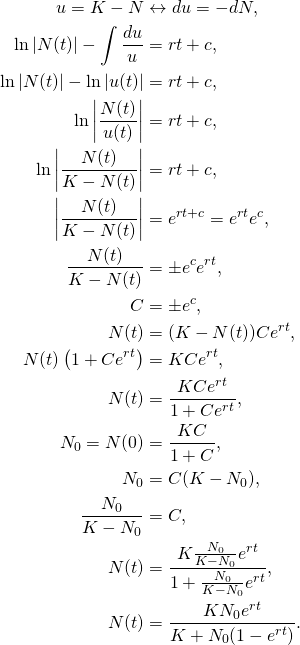
There. Breathe. I’ll have you know that out of those 21 steps that 15 of them are strictly algebra (just a hair under 75%).
The point, to bring us back to it, is that I was shown an equation where everything has real life meaning and the solution was a fun journey through using multiple tools (separation of variables – a change of differential notation, partial fraction decomposition, linearity of integral operator, integration by substitution, knowledge of transcendentals like ![]() and exponentiation, and fancy
and exponentiation, and fancy ![]() obfuscation)and a lot of my knowledge. I could sketch the solution and understand what it meant. I could consider the limiting behavior explicitly or qualitatively. I loved this thing. I loved it. Loved. Past tense. But the funny thing was that I would not fall out of love for a number of years and in the interim my admiration of this equation would only grow, but that is for another time.
obfuscation)and a lot of my knowledge. I could sketch the solution and understand what it meant. I could consider the limiting behavior explicitly or qualitatively. I loved this thing. I loved it. Loved. Past tense. But the funny thing was that I would not fall out of love for a number of years and in the interim my admiration of this equation would only grow, but that is for another time.